
|
|
ГОУ ВПО «Пермский государственный университет»Кафедра математического анализа СПРАВОЧНИК ПО ТЕМЕ "НЕПРЕРЫВНОСТЬ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ"
Пермь 2008 4.1 Понятие непрерывности функции 1. Нахождение приращения функции. Понятия:
1. Приращение аргумента, приращение функции Пусть дана функция
Умения:
1) Чему равно приращение функции Решение
Ответ:
2) Чему должно быть равно приращение аргумента, чтобы приращение Решение
Ответ:
3) Чему равно Приращение функции Решение
Ответ:
4) Чему должно быть равно значение Решение
Ответ: 2. Определения непрерывности функции в точке.
Понятия:
Окрестность точки из 1. Интервал вида 2. 3.
2. Непрерывность функции может быть задана разными определениями: 1. Формальное определение: Функцию 2. По Гейне (на языке последовательностей): Функция 3. По Коши (на языке “ 4. На языке приращений: Функция
Утверждения:
Алгоритм исследования функции на непрерывность в 1. Фиксируют произвольное 2. Оценивают 3. Решают неравенство 4. Фиксируют произвольное решение неравенства
Умения:
1) На языке Решение. 1. Зафиксируем 2. Рассмотрим выражение 3. Решим неравенство: 4.
2) С помощью определения на языке последовательности доказать непрерывность функции Решение.
2.
Тогда функция При нахождении предела мы пользовались теоремами о пределе суммы и произведения двух сходящихся числовых последовательностей.
3) Исследовать функцию Решение.
Значит, функция
4) Исследовать функцию Решение.
Т. к. 3 Нахождение
Понятия:
Окрестность точки из 1. Интервал вида 2. 3.
2. Непрерывность функции Коши (на языке “
Утверждения:
Алгоритм решения данного рода задач: 1. Фиксируют 2. Оценивают 3. Решают неравенство 4. Фиксируют произвольное решение неравенства
Умения:
1) Чему равно наибольшее Решение Рассмотрим Т.к. Ответ:
2) Чему равно наибольшее Решение Рассмотрим Т.к. Ответ:
3) Чему равно наибольшее Решение Рассмотрим Т.к. Ответ:
4. Непрерывность функции слева, справа; связь между односторонней непрерывностью функции в точке и непрерывностью функции в точке.
Понятия:
3. Непрерывность в точке слева, справа (односторонняя непрерывность) Функция
Утверждения:
Cвязь между односторонней непрерывностью функции в точке и непрерывностью функции в точке 1. Если 2. Если в точке 3. Если
Умения:
1) Существует ли Решение Данной функции не существует, для подтверждения рассмотрим последовательность Ответ: нет, не существует.
2) Существует ли Решение Рассмотрим функцию Очевидно, что Ответ: существует. Данные примеры иллюстрируют то, что не нужно путать односторонние пределы и одностороннюю непрерывность.
3) Показать, что Решение Т.к. 5. Точки разрыва и их классификация.
Понятия:
5. Разрывность в точке Функция 1. 2. 3. 4. 6. Точки разрыва первого и второго рода Точки разрыва, в которых существует конечное предельное значение, называются точками обыкновенного разрыва или точками разрыва первого рода. Точки разрыва, в которых не существует предельное значение функции или один из односторонних пределов равен бесконечности, называются точками бесконечного разрыва. 7. Скачок в точке разрыва Если 8. Точка устранимого разрыва Если Остальные точки являются точками неустранимого разрыва. 9. Точки бесконечного разрыва Точки разрыва второго рода, в которых хотя бы один из односторонних пределов равен бесконечности, называются точками бесконечного разрыва.
Умения:
1) Определить точки разрыва функции
Решение. Перепишем функцию в виде Рассмотрим точку
Значит, точка Рассмотрим точку
Случай аналогичен предыдущему, Значит, функция
2) Определить точки разрыва и их характер для функции Решение. В точке Функция
3) Определить точки разрыва и их характер для функции Решение. В точке Функция
4) Определить точки разрыва и их характер дл функции Решение. В точке 6. Нахождение скачка функции в точке.
Понятия:
7. Скачок в точке разрыва Если
Умения:
1) Чему равен скачок функции Решение
Ответ: 0
2) Чему равен скачок функции Решение
Ответ: 2
3) Чему равен скачок функции Решение
Ответ: 1
7. Исследование на непрерывность функции заданной графически.
Понятия:
2. Непрерывность функции 1. Формальное определение: Функцию
4. Непрерывность функции на множестве, в частности, на сегменте
Утверждения:
Наличие графика позволяет определить несколько правил, значительно облегчающих процесс исследования функции на непрерывность: 1. Посмотреть наличие выколотых точек графика функции (без скачка), тогда эти точки будут являться точками устранимого разрыва. 2. Проверить наличие скачка графика функции. Точка, в которой происходит скачок, является точкой разрыва первого рода. 3. Проверить наличие вертикальных асимптот графика функции. Если К сожалению, это правила не покрывают все виды точек разрыва, т.к. на графике достаточно сложно изобразить случай, когда предел функции не существует.
Умения:
1) При каком
Ответ: при
2) Среди данных четырех функций укажите номер той, которая не отвечает свойству остальных трех
Ответ: функция под номером 2, т.к. она непрерывна в отличие от трех остальных. 8. Исследование явно заданной функции на непрерывность в точке.
Понятия:
2. Непрерывность функции 1. Формальное определение: Функцию
Утверждения:
В данном случае точками разрыва являются точки, в которых функция не определена, в которых предельное значение равно бесконечности, не существует или оно отличено от значения функции в данной точке.
Умения:
1) Исследовать функцию Решение. Фиксируем произвольную
2) Какая из перечисленных функций непрерывна в 1. 2. 3. 4. Решение 1. 2.
3. 4. Ответ 4.
3) Какие из перечисленных функций непрерывны в 1. 2. 3. 4. Решение 1. 2. 3. 4. Ответ 3,4. 9. Исследование кусочно-заданной функции на непрерывность.
Понятия:
2. Непрерывность функции 1. Формальное определение: Функцию
4. Непрерывность функции на множестве, в частности, на сегменте
5. Разрывность в точке Функция 1. 2. 3. 4. 6. Точки разрыва первого и второго рода Точки разрыва, в которых существует конечное предельное значение, называются точками обыкновенного разрыва или точками разрыва первого рода. Точки разрыва, в которых не существует предельное значение функции или один из односторонних пределов равен бесконечности, называются точками бесконечного разрыва. 7. Скачок в точке разрыва Если 8. Точка устранимого разрыва Если Остальные точки являются точками неустранимого разрыва. 9. Точки бесконечного разрыва Точки разрыва второго рода, в которых хотя бы один из односторонних пределов равен бесконечности, называются точками бесконечного разрыва.
Утверждения:
Если
В случае кусочно-заданной функции точками разрыва являются точки, в которых функция не определена, в которых предельное значение равно бесконечности, не существует или оно отличено от значения функции в данной точке, также точками подозрительными на разрыв являются точки “стыка”.
Умения: 1) Определить, является ли непрерывной функция Решение. Рассмотрим точку стыка
Т.к. Во всех остальных точка функция непрерывна, значит 2) Определить точки разрыва и их характер для функции Решение. Рассмотрим точки стыка:
3) Определить точки разрыва и их характер для функции Решение. В данном случае все точки являются точками стыка. Рассмотрим произвольную точку В точках В точках
4) Определить точки разрыва и их характер для функции Решение. Данная функция носит название функции Дирихле и является разрывной в каждой точке, причем все точка разрыва второго рода. В точках В точках
5) Существует ли функция, непрерывная в одной точке и разрывная во всех остальных? Решение. Существует, эта функция:
Действительно, подобно функции Дирихле она разрывна во всех точках, кроме
6) На каком промежутке непрерывна функция Решение.
Здесь только две точки стыка
10. Доопределение функции в точке по непрерывности.
Понятия:
2. Непрерывность функции 1. Формальное определение: Функцию
6. Точки разрыва первого и второго рода Точки разрыва, в которых существует конечное предельное значение, называются точками обыкновенного разрыва или точками разрыва первого рода. Точки разрыва, в которых не существует предельное значение функции или один из односторонних пределов равен бесконечности, называются точками бесконечного разрыва.
8. Точка устранимого разрыва Если Остальные точки являются точками неустранимого разрыва.
Умения:
1) Доопределить функцию Решение. Эта функция не определена в точке
Следовательно, точка Чтобы устранить разрыв доопределим нашу функцию в этой точке и положим
2) Доопределить функцию Решение. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 . Обозначим
. Обозначим  .
.  - называется приращением аргумента.
- называется приращением аргумента. 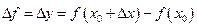 , где
, где  - приращение функции
- приращение функции  в точке
в точке 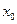 соответствующее приращению аргумента
соответствующее приращению аргумента  в точке
в точке  при
при  ?
?
 .
. в точке
в точке  ?
? , отсюда
, отсюда 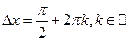
 при переходе аргумента от значения
при переходе аргумента от значения  к значению
к значению  ?
?
 .
. при изменении аргумента
при изменении аргумента  от
от  до
до  равно 2?
равно 2? , отсюда
, отсюда 

 , с центром в точке
, с центром в точке  , где
, где  , называют
, называют  - окрестностью точки
- окрестностью точки  .
. .
. .
. называют непрерывной в точке
называют непрерывной в точке 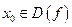 если
если 
 непрерывна в точке
непрерывна в точке 
 ”): Функция
”): Функция 

 на языке “
на языке “  и
и  .
. сверху функцией
сверху функцией  .
. .
. доказать непрерывность функции
доказать непрерывность функции 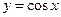 в произвольной точке
в произвольной точке  .
. . И, пользуясь тем, что
. И, пользуясь тем, что  и
и 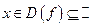 получим оценку сверху некоторой функцией
получим оценку сверху некоторой функцией 
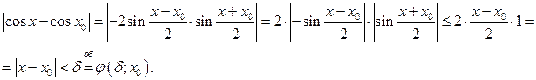 Здесь мы воспользовались тем, что
Здесь мы воспользовались тем, что  .
. , т.е.
, т.е. 
 , например
, например  . Значит, функция
. Значит, функция  ,
,  и
и  в произвольной точке
в произвольной точке  1. Берем произвольную точку
1. Берем произвольную точку  .
.
 .
. на непрерывность в точке
на непрерывность в точке  , пользуясь определением на языке приращений.
, пользуясь определением на языке приращений. .
. 
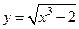 на непрерывность в точке
на непрерывность в точке  ,
, .
. , то функция
, то функция  для непрерывной в точке
для непрерывной в точке  такое, что из неравенства
такое, что из неравенства  следует неравенство
следует неравенство  ?
?
 ,
,  , значит наибольшее
, значит наибольшее 
 такое, что из неравенства
такое, что из неравенства  следует неравенство
следует неравенство  ?
? , тогда
, тогда  ,
,  , и
, и  .
. , значит наибольшее
, значит наибольшее 
 такое, что при любом
такое, что при любом 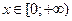 из неравенств
из неравенств  ?
?
 .
.
 - справа
- справа - слева
- слева или
или  . Обратное в общем говоря не верно (например,
. Обратное в общем говоря не верно (например, 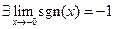 , но не существует
, но не существует  ).
). равны, то в точке
равны, то в точке  ,
,  и
и  , то
, то  такая, что
такая, что  и
и  ?
? , данная последовательность удовлетворяет всем условиям определения непрерывности по Гейне, но очевидно, что
, данная последовательность удовлетворяет всем условиям определения непрерывности по Гейне, но очевидно, что  не имеет предела, значит
не имеет предела, значит  но
но 
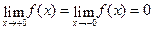 , но, т.к.
, но, т.к.  , то функция разрывна.
, то функция разрывна. непрерывна слева на
непрерывна слева на  ?
? , значит и
, значит и  , что и свидетельствует о непрерывности функции
, что и свидетельствует о непрерывности функции 
 или
или  .
.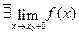 или
или 
 или
или 
 ,тогда говорят, что функция терпит скачок в точке
,тогда говорят, что функция терпит скачок в точке  .
.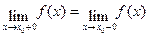 и
и  . в некоторых случаях нам следует изменить значение функции в точке
. в некоторых случаях нам следует изменить значение функции в точке 

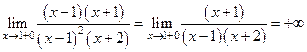
 .
.
 - точка разрыва второго рода.
- точка разрыва второго рода. имеет точки разрыва
имеет точки разрыва  ,
,  .
.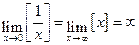 , значит
, значит  разрывна в точках
разрывна в точках  , тогда исследуемая функция терпит разрыв в точках
, тогда исследуемая функция терпит разрыв в точках  . Зная свойства функции
. Зная свойства функции  ,
,  , т.к.
, т.к.  значит
значит  разрывна в точке
разрывна в точке  , т.е.
, т.е.  . Это точки неустранимого разрыва.
. Это точки неустранимого разрыва.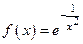 ,
,  , значит
, значит  в точке
в точке 
 , значит скачок равен
, значит скачок равен 
 в точке
в точке 
 , значит скачок равен
, значит скачок равен 
 в точке
в точке 
 , значит скачок равен
, значит скачок равен 
 , если она непрерывна в каждой точке данного множества, т.е:
, если она непрерывна в каждой точке данного множества, т.е:  .
. -вертикальная асимптота, то
-вертикальная асимптота, то  , график которой изображен на рисунке, определена, имеет правый предел, непрерывна слева, разрывна справа?
, график которой изображен на рисунке, определена, имеет правый предел, непрерывна слева, разрывна справа?
 , т.к. именно в этой точке функция удовлетворяет выше заданным требованиям, в отличие от других точек:
, т.к. именно в этой точке функция удовлетворяет выше заданным требованиям, в отличие от других точек:  ,
,  и
и 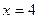 , в которых она разрывна слева.
, в которых она разрывна слева.
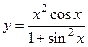 на непрерывность в
на непрерывность в  , значит, функция
, значит, функция  .
.




 ,
,  , разрывна.
, разрывна.



 - разрывна, т.к.
- разрывна, т.к.  .
. .
. .
.



 .
.
 , значит все точки стыка – точки бесконечного разрыва. В остальных же точках
, значит все точки стыка – точки бесконечного разрыва. В остальных же точках 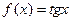 - непрерывна.
- непрерывна.
 ,
,  , а значит на лицо разрыв второго рода.
, а значит на лицо разрыв второго рода. :
:  , а значит
, а значит  и это также точки разрыва второго рода.
и это также точки разрыва второго рода. функция будет непрерывной, для этого рассмотрим
функция будет непрерывной, для этого рассмотрим 
 .
.
 , что и свидетельствует о том, что разрывы второго рода.
, что и свидетельствует о том, что разрывы второго рода. , а значит
, а значит 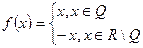 .
. , в которой левый и правый пределы совпадают и равны нулю.
, в которой левый и правый пределы совпадают и равны нулю. ?
?
 .
. , значит в точке
, значит в точке  функция терпит разрыв. Аналогичным образом доказывается, что и в точке
функция терпит разрыв. Аналогичным образом доказывается, что и в точке 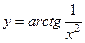 так, чтобы она стала непрерывной.
так, чтобы она стала непрерывной. ,
,  .
. .
. так, чтобы она стала непрерывной.
так, чтобы она стала непрерывной.