
|
|
Непрерывное начисление сложных процентов
При вычислении результата инвестирования могут использоваться различные периоды начисления сложных процентов. Например, законы могут налагать ограничения на фиксированную ставку выплат, но не налагать ограничений на периоды начисления. Такова была ситуация в начале 1975 г., когда ставка процентных выплат по займам и депозитам сроком от шести до десяти лет была ограничена на уровне 7,75% годовых. Первоначально по большинству займов и накоплений выплачивались простые проценты. При этом $1, вложенный в начале года, вырастал до $1,0775 к концу года. Позже, в целях привлечения вкладчиков, некоторые учреждения объявили, что они будут выплачивать 7,75% годовых, но производить полугодовое начисление сложных процентов по ставке 3,875% (7,75%/2). Это означает, что $1, вложенный в начале года, вырастет до $1,03875 через 6 месяцев, а еще через 6 месяцев эта величина вырастет до $1,079 ($1,03875 х 1,03875), что будет означать эффективную ставку 7,9% за год. Эта процедура не считалась нарушением закона. Вскоре другие учреждения предложили 7,75% годовых, пересчитываемых ежеквартально (т.е. 7,75%/4 = 1,938% в квартал), что означало эффективную процентную ставку 7,978% за год. Затем другие предложили пересчитывать годовую ставку 7,75% ежемесячно (7,75%/12 = 0,646% в месяц), что давало эффективную годовую ставку 8,031%. Предел был достигнут, когда одна компания предложила непрерывное начисление годовой ставки 7,75%. Если r означает годовую ставку сложных процентов (в нашем случае 7,75%), а n – количество начислений за год, то эффективная годовая ставка определяется выражением:
где re – эффективная годовая процентная ставка. Таким образом, при полугодовом начислении сложных процентов с годовой ставкой 7,75% получаем:
а при квартальном начислении:
и т.д. По мере того как интервалы начислений уменьшаются, их число (я) увеличивается, а также увеличивается эффективная процентная ставка re. Математически доказывается, что при росте п величина [1 + (r/n)]n стремится к еr, где е - константа, равная 2,71828 с точностью до пяти знаков. В нашем примере e0,0775 = 1,0806, что означает эффективную годовую ставку 8,06%15. Может быть получена и более общая формула непрерывного начисления. Пусть при годовой ставке r при непрерывном начислении Р долларов вырастают до Ft долларов через t лет, тогда соотношение этих величин будет следующим:
Аналогично нынешняя стоимость Ft долларов, которые будут получены через t лет при непрерывном начислении с годовой ставкой r, равна:
Таким образом, если спот-ставки выражаются как годовые ставки при непрерывном начислении сложных процентов, то коэффициенты дисконтирования dt могут быть подсчитаны следующим образом:
Последние три формулы могут применяться при любых значениях t, включая дробные значения (например, если Ft будет получено через 2,5 года, то t = 2,5).
Примечание
1 Это вычисление подразумевает, что облигация не будет продана досрочно. Если предположить, что облигация будет продана, как только это станет возможным, то ставка в коэффициенте дисконтирования, приравнивающая текущую стоимость соответствующих выплат к текущей рыночной цене облигации, называется доходностью к отзыву (yield to call). 2 Заметьте, что, используя уравнение (5.24), мы получим ra = 1,039232 - 1 = 8%, т.е. то же значение, которое получается из уравнения (5.22). 3 Подумайте, что случится, если будет произвольно увеличиваться число периодов начисления сложных процентов в одном году так, чтобы каждый из интервалов становился очень малым. В пределе получится бесконечно большое число бесконечно малых интервалов, т.е. ситуация непрерывного начисления, которая обсуждается в Приложении. 4 Иногда кривая доходности может иметь «горбы», где она ненадолго возрастает, а затем убывает, возможно, выравниваясь между средними и большими сроками погашения. 5 Не так давно была разработана «современная теория ожиданий», которая является более логичной экономически, чем теория непредвзятых ожиданий. Однако из нее следуют выводы и объяснения поведения временной зависимости, аналогичные тем, что следовали из теории непредвзятых ожиданий. Учитывая их сходство, была приведена только теория непредвзятых ожиданий. 6 Уравнение (5.25) может быть записано в более общем виде так: 7 См. уравнения (5.1) - (5.3) и гл. 13 для выяснения природы взаимоотношений номинальных ставок, реальных ставок и уровня ожидаемой инфляции. 8 К сожалению, этот риск часто называют «риском ликвидности» (liquidity risk), тогда как по смыслу более подходит название «риск изменения процентной ставки» (price risk), потому что именно изменчивость ставок, сопутствующая долгосрочным ценным бумагам, представляет проблему для инвестора. Отчасти данный риск компенсируется риском, присутствующим при применении «стратегии возобновления» вместо «стратегии покупки до погашения», а именно риском, связанным с неопределенностью спот-ставки в конце первого года, по которой будет осуществляться дальнейшее инвестирование. Теория наилучшей ликвидности предполагает, что этот риск относительно мал и не столь важен для инвестора. 9 Иногда эту разницу называют премией за срочность (term premium). Смотрите статью Брэвфорда Корнелла «Измерение премии за срочность: практические наблюдения» (Bradford Cornell, «Measuring the Term Premium: An Empirical Note», Journal of Economics and Business, 42, no. 1 (February 1990), pp. 89-92). 10 Следует заметить, что, хотя форвардная ставка может быть определена, и ожидаемая слот-ставка, и премия за ликвидность могут оказаться неопределенными. Все, что можно сделать, – это попытаться оценить их значения. 11 Уравнение (5.27) может быть записано в более общем виде:
Так как
12 Если бы es1,2 была больше или равна s1, то неравенство бы не выполнялось, так как предполагалось бы, что s1 > s2. 13 Более умеренная версия называется теория наилучшей среды обитания (preferred habitat theory), по которой заемщики и инвесторы могут покинуть свой сегмент рынка (определяемый сроком погашения обязательств) только при условии, что разница между доходностями в различных сегментах достаточно велика. 14 Эмпирические наблюдения не являются бесспорными. Фама утверждает, что факты не соответствуют ни теории непредвзятых ожиданий, ни теории наилучшей ликвидности, тогда как Маккалок опровергает аргументы Фамы и склоняется в пользу последней теории. См.: Eugene F. Fama, «Term Premiums in Bond Returns», Journal of financial Economics, 13, no. 4 (December 1984), pp. 529-546; J. Huston McCulloch, «The Monotonicity of the Term Premium: A Closer Look», Journal of Finacial Economics, 18, no. 1 (March 1987), pp. 185-192; «An Estimate of the Liquidity Premium», Journal of Political Economy, 83, no. 1 (February 1975), pp. 95-119; взгляды Маккалока отражены также в работе: Matthew Richardson, Paul Richardson, Tom Smith, «The Monotonicity of the Term Premium: Another Look», Journal of Financial Economics, 31 no 1 (February 1992), pp. 97-105. 15 Для подобных вычислений могут быть использованы таблицы натуральных логарифмов. Натуральный логарифм 1,0806 равен 0,0775, а антилогарифм 0,0775 равен 1,0806.
Ключевые термины
доходность к погашению спот-ставка коэффициенты дисконтирования рыночная функция дисконтирования дисконтирование форвардная ставка начисление сложных процентов годовая процентная ставка кривая доходности временная зависимость теория непредвзятых ожиданий теория наилучшей ликвидности премия за ликвидность сегментация рынка
Глава 6

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|

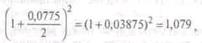

 (5.31)
(5.31)

 . Таким образом, используя уравнение (5.19), теория непредвзятых ожиданий утверждает, что
. Таким образом, используя уравнение (5.19), теория непредвзятых ожиданий утверждает, что 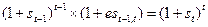 .
. Таким образом, используя уравнение (5.19), теория наилучшей ликвидности утверждает, что:
Таким образом, используя уравнение (5.19), теория наилучшей ликвидности утверждает, что:
 > 0, то отсюда следует, что:
> 0, то отсюда следует, что: