
|
|
Свойства выборочного коэффициента корреляции1. Абсолютная величина выборочного коэффициента корреляции не превосходит 1 ( 2. Если выборочный коэффициент корреляции равен 0 и выборочные линии регрессии – прямые линии, то В этом случае прямые линии регрессии параллельны соответственно координатным осям. Замечание. Если выборочный коэффициент корреляции 3. Если абсолютная величина 4. С возрастанием абсолютной величины выборочного коэффициента корреляции линейная корреляционная зависимость становится более тесной и при Величина коэффициента корреляции характеризует силу линейной связи между признаками ( если если если если если если 5. Знак выборочного коэффициента корреляции совпадает со знаком выборочного коэффициента регрессии: Перемножим первое и второе равенства Знак при радикале должен совпадать со знаком коэффициента регрессии, т.е. Выборочный коэффициент корреляции равен среднему геометрическому выборочных коэффициентов регрессий. Точечная и интервальная оценки коэффициентов корреляции нормально распределенной генеральной совокупности Если выборка имеет достаточно большой объем Для интервальной оценки коэффициента корреляции нормально распределенной генеральной совокупности (
Проверка гипотезы о значимости выборочного коэффициента корреляции Пусть двумерная генеральная совокупность Так как выборка отобрана случайно, то еще нельзя заключить, что коэффициент корреляции генеральной совокупности Нас интересует именно этот коэффициент Если гипотеза будет опровергнута, то это означает, что выборочный коэффициент корреляции значительно отличается от 0, а Если нулевая гипотеза будет принята, то выборочный коэффициент корреляции не значим, а В качестве критерия проверки нулевой гипотезы примем случайную величину Величина Для того чтобы при заданном уровне значимости Если Корреляционное отношение Ранее рассматривалась теснота линейной корреляционной связи. Вопрос: как оценить тесноту любой корреляционной связи? Так как все значения признака
Определение. Групповой дисперсией называют дисперсию значений признака, принадлежащих группе, относительно групповой средней.
где Определение. Внутригрупповой дисперсией называют среднюю арифметическую групповых дисперсий, взвешенную по объемам групп.
Определение. Межгрупповой дисперсией называют дисперсию групповых средних относительно общeй средней.
где Определение. Общей дисперсией называют дисперсию значений признака всей совокупности относительно общей признака.
Для оценки тесноты нелинейной корреляционной связи вводят корреляционные характеристики: 1)
2)

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
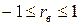 ).
). и
и  не связаны линейной корреляционной зависимостью и
не связаны линейной корреляционной зависимостью и  ,
,  .
. , то признаки
, то признаки  , то наблюдаемые значения признаков связаны линейной функциональной зависимостью.
, то наблюдаемые значения признаков связаны линейной функциональной зависимостью. – связь слабая;
– связь слабая; – связь умеренная;
– связь умеренная; – связь заметная;
– связь заметная; – связь высокая;
– связь высокая; – связь весьма высокая;
– связь весьма высокая; ,
,  и определяет направление связи. Если
и определяет направление связи. Если  – связь прямая,
– связь прямая,  – связь обратная.
– связь обратная.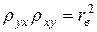 ;
; 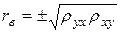 .
. ;
;  .
. и хорошо представляет генеральную совокупность, то заключение о тесноте линейной зависимости между признаками, полученное по данным выборки, в известной степени может быть распространено на генеральную совокупность. В качестве точечной оценки коэффициента корреляции генеральной совокупности берут
и хорошо представляет генеральную совокупность, то заключение о тесноте линейной зависимости между признаками, полученное по данным выборки, в известной степени может быть распространено на генеральную совокупность. В качестве точечной оценки коэффициента корреляции генеральной совокупности берут  .
.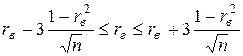 . (8)
. (8) и по ней найден выборочный коэффициент корреляции
и по ней найден выборочный коэффициент корреляции 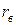 , который оказался отличным от 0.
, который оказался отличным от 0.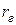 также отличен от 0.
также отличен от 0. о равенстве нулю генерального коэффициента корреляции при конкурирующей гипотезе
о равенстве нулю генерального коэффициента корреляции при конкурирующей гипотезе  .
. , где
, где  при справедливости нулевой гипотезы имеет распределение Стьюдента с
при справедливости нулевой гипотезы имеет распределение Стьюдента с  степенями свободы. Обозначим значение критерия, вычисленное по данным наблюдений через
степенями свободы. Обозначим значение критерия, вычисленное по данным наблюдений через  и сформулируем правило проверки нулевой гипотезы.
и сформулируем правило проверки нулевой гипотезы.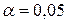 проверить нулевую гипотезу
проверить нулевую гипотезу  и по таблице критических точек распределения Стьюдента по заданному уровню значимости
и по таблице критических точек распределения Стьюдента по заданному уровню значимости  и числу степеней свободы
и числу степеней свободы  для двусторонней критической области.
для двусторонней критической области. – нет основания отвергнуть нулевую гипотезу. Если
– нет основания отвергнуть нулевую гипотезу. Если  – нулевую гипотезу отвергают и, следовательно, выборочный коэффициент корреляции значимо отличается от 0 , то есть
– нулевую гипотезу отвергают и, следовательно, выборочный коэффициент корреляции значимо отличается от 0 , то есть  . (9)
. (9) , (10)
, (10) – частота значений
– частота значений  при
при  ,
,  – номер группы,
– номер группы,  ,
,  – групповая средняя группы
– групповая средняя группы  – объем группы
– объем группы  , (11)
, (11) , (12)
, (12) – общая средняя.
– общая средняя. . (13)
. (13) – выборочное корреляционное отношение
– выборочное корреляционное отношение  (14)
(14) – выборочное корреляционное отношение
– выборочное корреляционное отношение  (15)
(15)