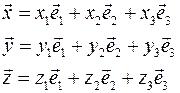Векторы и смешанное произведение
Определение 35
Упорядоченная тройка некомпланарных векторов называется правой, если при отложенных векторах из одной точки из конца вектора  поворот вектора поворот вектора  к вектору к вектору  по наименьшему углу виден против часовой стрелки. В противном случае тройка векторов называется левой. по наименьшему углу виден против часовой стрелки. В противном случае тройка векторов называется левой.
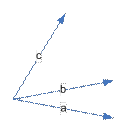
(правая тройка – 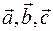 , левая тройка – , левая тройка –  ) )
Замечание.
Если 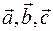 - правая тройка векторов, то - правая тройка векторов, то 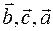 и и  - тоже правые тройки, а - тоже правые тройки, а  , ,  и и  - левые. - левые.
Определение 36
Две тройки векторов будем называть одинаково ориентированными, если они одновременно либо правые, либо левые.
Замечание.
Все некомпланарные тройки векторов распадаются на два класса – класс правых троек и класс левых троек.
Определение 37
Говорят, что в пространстве задана ориентация, если выбран из вышеупомянутых классов. Обычно работать будем в пространстве, где ориентация задается правой тройкой векторов.
Определение 38
Пусть в пространстве задана ориентация правыми тройками. Векторным произведением векторов  и и  называется вектор называется вектор  , такой что , такой что
1) 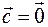 , если , если  и и  коллинеарны коллинеарны
2) если  и и  неколлинеарны, то неколлинеарны, то 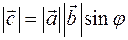 , где , где 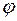 угол между угол между  и и 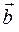 и и 
3) тройка векторов 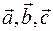 имеет такую же ориентацию, как и пространство. имеет такую же ориентацию, как и пространство.
Геометрические свойства векторного произведения
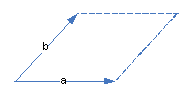  равен площади параллелограмма, натянутого на векторы равен площади параллелограмма, натянутого на векторы  и и  . .
Теорема 18 (критерий коллинеарности)
Вектора  и и  коллинеарны коллинеарны 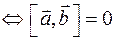 . .
Доказательство.
 Если Если  и и  коллинеарны, то по определению коллинеарны, то по определению  . .
 Если Если  , то , то
1) В случае 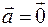 или или 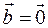 произведение произведение  , вектора коллинеарны. , вектора коллинеарны.
2) В случае 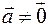 и и 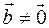  , т.е. , т.е. 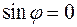 . Значит . Значит 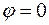 или или  . Векторы . Векторы  и и  коллинеарны. коллинеарны.
Определение 39
Смешанным произведением векторов  , ,  и и  называется выражение называется выражение  . Обозначение . Обозначение 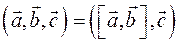 . .
Геометрические свойства смешанного произведения.
Смешанное произведение векторов 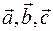 равно объему параллелепипеда, построенного на векторах равно объему параллелепипеда, построенного на векторах 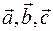 , отложенных из одной точки, взятый со знаком «+», если тройка , отложенных из одной точки, взятый со знаком «+», если тройка 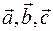 - правая, со знаком «–», если левая. - правая, со знаком «–», если левая.
Доказательство.
 Если Если 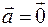 или или 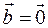 или или 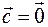 , то утверждение выполняется. Если , то утверждение выполняется. Если  и и  коллинеарны, то коллинеарны, то  и объем параллелепипеда тоже равен и объем параллелепипеда тоже равен 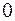 . Пусть . Пусть  и и  неколлинеарны. Тогда тройка неколлинеарны. Тогда тройка  является правой. является правой. 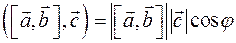 . . 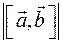 - площадь основания параллелепипеда. - площадь основания параллелепипеда. 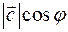 - высота параллелепипеда, поэтому - высота параллелепипеда, поэтому 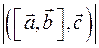 равен объему параллелепипеда. Если равен объему параллелепипеда. Если 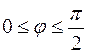 , то тройка векторов , то тройка векторов 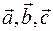 - правая и - правая и 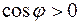 . Если . Если  , то тройка векторов , то тройка векторов 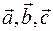 - левая и - левая и 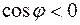 . Значит . Значит  , где , где 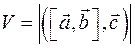 . .
Теорема 19 (критерий компланарности)
Векторы 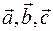 являются компланарными являются компланарными 
Доказательство.
 Если векторы компланарны, то вектор Если векторы компланарны, то вектор 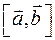 ортогонален векторам ортогонален векторам  и и  , а значит ортогонален вектору , а значит ортогонален вектору  . .
 Если Если  , то , то 
Если  , то , то  и и  коллинеарны. коллинеарны. 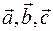 компланарны. В случае компланарны. В случае 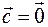 , , 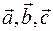 компланарны. В случае, когда компланарны. В случае, когда  вектор вектор  лежит в плоскости векторов лежит в плоскости векторов  и и  . .
Свойства смешанного произведения.
 выполняются: выполняются:
1) 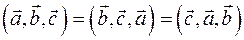
2) 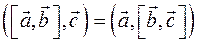
3) 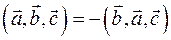
4)  . .
Доказательство.
1) Тройки векторов 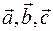 , , 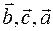 , ,  - либо все компланарны, либо все одновременно правые, либо все одновременно левые. Если они компланарны, то - либо все компланарны, либо все одновременно правые, либо все одновременно левые. Если они компланарны, то  . Если одни одновременно правые, то . Если одни одновременно правые, то 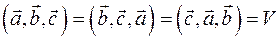 . Если они одновременно левые, то . Если они одновременно левые, то  , где , где 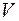 - объем параллелепипеда, построенного на векторах - объем параллелепипеда, построенного на векторах 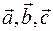 . .
2)  . .
3) Тройки векторов 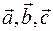 и и  имеют разную ориентацию и имеют разную ориентацию и  . Поэтому . Поэтому 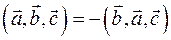 . .
4) 

Свойства векторного произведения.
Для любых векторов 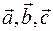 и любых чисел и любых чисел  выполняются свойства: выполняются свойства:
1) 
2) 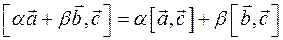
3) 
Доказательство.
Лемма.
Если для любого вектора  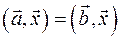 , то , то 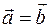 . .
Доказательство.
Если 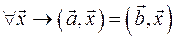 , то , то  и при и при  . Тогда . Тогда  , т.е. , т.е.  , значит , значит 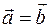 . .
1) Из свойств смешанного произведения для всех  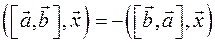
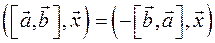 . Поэтому . Поэтому  . .
2) Из свойств смешанного произведения для всех 
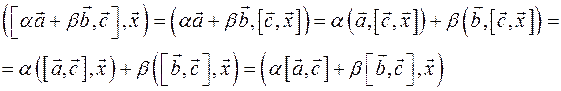
Т.е. для всех   . Поэтому . Поэтому 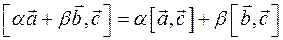 . .
3) Следует из определения.
Замечание.
Из свойств 1) и 2) легко доказывается (аналогично доказательству для скалярного произведения) линейность векторного произведения по второму аргументу.
Определители
Определение 40
Набор элементов  , где , где  называется матрицей размерностью называется матрицей размерностью  . Обычно матрицу записывают в виде таблицы. . Обычно матрицу записывают в виде таблицы.
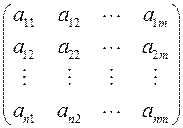
Для матриц  с элементами из чисел, функций, можно дать понятие определителя матрицы. с элементами из чисел, функций, можно дать понятие определителя матрицы.
Для матрицы 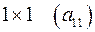 определителем называется число определителем называется число  . Обозначается . Обозначается 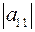 . .
Для матрицы  определителем называется число определителем называется число 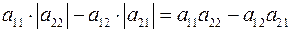 . Обозначается . Обозначается  . .
Для матрицы  определителем называется число определителем называется число 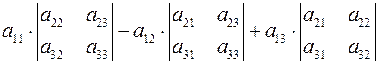 . Обозначается . Обозначается  . .
Выражение векторного произведения в ортонормированном базисе.
Пусть 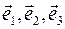 - ортонормированный базис, являющийся правой тройкой. Тогда - ортонормированный базис, являющийся правой тройкой. Тогда 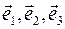 , , 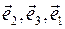 и и  - правые тройки, - правые тройки, 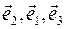 , ,  и и 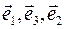 - левые тройки. Имеем - левые тройки. Имеем
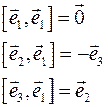 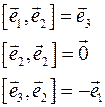 
Для векторов 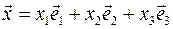 и и  имеем: имеем:

Выражение смешанного произведения в ортонормированном базисе.
Пусть 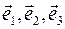 - ортонормированный базис, являющийся правой тройкой. - ортонормированный базис, являющийся правой тройкой.
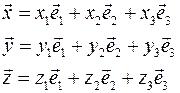

Следствие.
Три вектора компланарны тогда и только тогда, когда определитель матрицы, составленной из их координат равен 0.
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|


 поворот вектора
поворот вектора  к вектору
к вектору  по наименьшему углу виден против часовой стрелки. В противном случае тройка векторов называется левой.
по наименьшему углу виден против часовой стрелки. В противном случае тройка векторов называется левой.
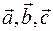 , левая тройка –
, левая тройка –  )
)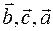 и
и  - тоже правые тройки, а
- тоже правые тройки, а  и
и  - левые.
- левые.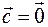 , если
, если 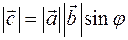 , где
, где 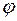 угол между
угол между 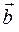 и
и 

 равен площади параллелограмма, натянутого на векторы
равен площади параллелограмма, натянутого на векторы 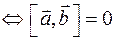 .
. Если
Если  .
. Если
Если 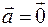 или
или 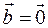 произведение
произведение 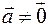 и
и 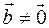
 , т.е.
, т.е. 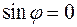 . Значит
. Значит 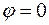 или
или  . Векторы
. Векторы  . Обозначение
. Обозначение 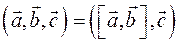 .
. Если
Если 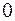 . Пусть
. Пусть  является правой.
является правой. 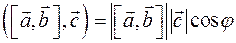 .
. 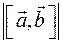 - площадь основания параллелепипеда.
- площадь основания параллелепипеда. 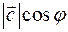 - высота параллелепипеда, поэтому
- высота параллелепипеда, поэтому 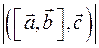 равен объему параллелепипеда. Если
равен объему параллелепипеда. Если 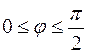 , то тройка векторов
, то тройка векторов 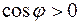 . Если
. Если  , то тройка векторов
, то тройка векторов 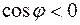 . Значит
. Значит  , где
, где 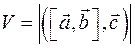 .
.
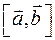 ортогонален векторам
ортогонален векторам  , то
, то 
 , то
, то  вектор
вектор  выполняются:
выполняются: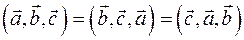
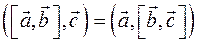
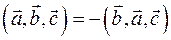
 .
. . Если одни одновременно правые, то
. Если одни одновременно правые, то 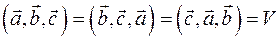 . Если они одновременно левые, то
. Если они одновременно левые, то  , где
, где 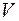 - объем параллелепипеда, построенного на векторах
- объем параллелепипеда, построенного на векторах  .
. . Поэтому
. Поэтому 

 выполняются свойства:
выполняются свойства:
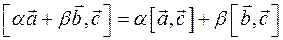


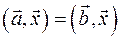 , то
, то 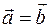 .
.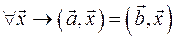 , то
, то  и при
и при  . Тогда
. Тогда  , т.е.
, т.е.  , значит
, значит 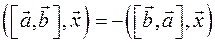
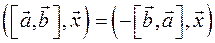 . Поэтому
. Поэтому 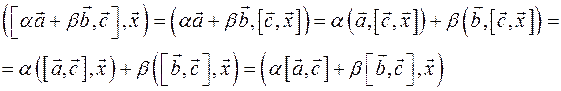
 . Поэтому
. Поэтому  , где
, где  называется матрицей размерностью
называется матрицей размерностью  . Обычно матрицу записывают в виде таблицы.
. Обычно матрицу записывают в виде таблицы.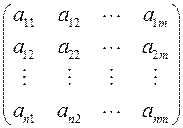
 с элементами из чисел, функций, можно дать понятие определителя матрицы.
с элементами из чисел, функций, можно дать понятие определителя матрицы.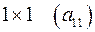 определителем называется число
определителем называется число  . Обозначается
. Обозначается 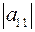 .
. определителем называется число
определителем называется число 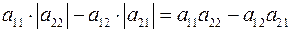 . Обозначается
. Обозначается  .
. определителем называется число
определителем называется число 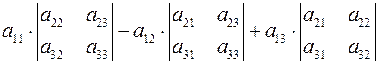 . Обозначается
. Обозначается  .
.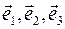 - ортонормированный базис, являющийся правой тройкой. Тогда
- ортонормированный базис, являющийся правой тройкой. Тогда 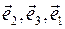 и
и  - правые тройки,
- правые тройки, 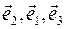 ,
,  и
и 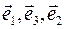 - левые тройки. Имеем
- левые тройки. Имеем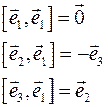
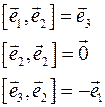

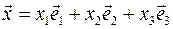 и
и  имеем:
имеем: