
|
|
Все аналогичные определения делаются для плоскости.Определение 24 Углом между векторами называется угол между любыми двумя их экземплярами, отложенными от одной точки. Определение 25 Декартовой системой координат называется система координат, в которой базис состоит из единичных векторов, попарно перпендикулярных друг другу. Определение 26 Пусть в пространстве задана система координат Определение 27 Пусть в пространстве задана система координат Замечание В декартовой системе координат проекция вектора Теорема 14 Проекцией суммы векторов является сумма проекций этих векторов. Проекцией произведения вектора на число является произведение проекции этого вектора и этого числа. Доказательство Пусть проекциями векторов Определение 28 Проекцией вектора
Такую проекцию называют ортогональной. Замечание Проекции векторов на координатные прямые в декартовой системе координат являются ортогональными. Определение 29 Если на прямой направление задается единичным вектором Теорема 15 Значение проекции вектора на прямую с единичным вектором Доказательство очевидно Замечание Из вышедоказанных теорем следует, что значение проекции суммы векторов равно сумме проекций, значение проекции произведения вектора на число равно произведению проекции вектора на это число. Определение 30 Скалярным произведением векторов Замечание Если хотя бы один из сомножителей является нулевым вектором, то скалярное произведение равно Замечание
Определение 31 Векторы Теорема 16 (свойства скалярного произведения) Скалярное произведение обладает следующими свойствами: 1) Замечание Из свойств 1) и 2) следуют свойства:
Для доказательства проведем выкладки:
Доказательство. 1) Очевидно (следует из определения). 2) Так как 3) Так как Определение 32 Базис Замечание. Базис в декартовой системе координат является ортонормированным. Теорема 17 Пусть
Тогда Доказательство. Используем свойства скалярного произведения.
Следствие. В ортонормированном базисе Доказательство.
Следствие. Косинус угла
Определение 33 Ортом вектора Утверждение. В ортонормированном базисе Определение 34 В ортонормированном базисе Замечание 1. Так как Замечание 2. Направляющие косинусы являются координатами орта
Замечание 3. Направляющие косинусы вектора Под направляющими косинусами вектора подразумеваются направляющие косинусы его орта. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 . Тогда множество точек
. Тогда множество точек  таких, что
таких, что  коллинеарен
коллинеарен  называется координатной прямой вектора
называется координатной прямой вектора  . Координатная прямая в направлении, задаваемом вектором
. Координатная прямая в направлении, задаваемом вектором  и
и  называется множество точек
называется множество точек  на координатную прямую вектора
на координатную прямую вектора  , где
, где  определяется из разложения
определяется из разложения  :
:  . Проекцией точки
. Проекцией точки  такая, что
такая, что  является проекцией вектора
является проекцией вектора  , где
, где  - угол между
- угол между  на координатную прямую
на координатную прямую  и
и  соответственно. Так как при сложении векторов из координаты складываются, то проекцией вектора
соответственно. Так как при сложении векторов из координаты складываются, то проекцией вектора 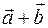 на координатную прямую является вектора
на координатную прямую является вектора  . Аналогично доказываются утверждение про произведение.
. Аналогично доказываются утверждение про произведение. на прямую называется вектор
на прямую называется вектор  , где точки
, где точки 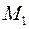 и
и  являются основаниями перпендикуляров, опущенных из точек
являются основаниями перпендикуляров, опущенных из точек 
 , то значение проекции вектора
, то значение проекции вектора 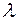 такое, что
такое, что  является ортогональной проекцией вектора
является ортогональной проекцией вектора  , где
, где 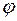 - угол между векторами
- угол между векторами  , где
, где  .
.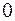 .
. тогда и только тогда, когда либо векторы перпендикулярны, либо один из них равен
тогда и только тогда, когда либо векторы перпендикулярны, либо один из них равен  .
.


 причем
причем  только если
только если 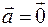 .
.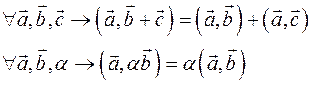

 и
и  является линейно по своему аргументу, то
является линейно по своему аргументу, то 
 .
. , то
, то  и
и  , т.е. когда
, т.е. когда  называется ортонормированным базисом, если
называется ортонормированным базисом, если 
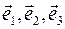 - ортонормированный базис.
- ортонормированный базис.
 .
.
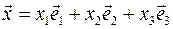 может быть вычислена по формуле
может быть вычислена по формуле  .
.
 в ортонормированном базисе
в ортонормированном базисе 
 .
. орт вектора
орт вектора 

 , то
, то
 .
.