
|
|
Специальной правой частью
Рассмотрим теперь неоднородное линейное рекуррентное соотношение второго порядка с постоянными коэффициентами f(n+2) = a1×f(n+1) + a2×f(n) + ln×Tm(n), где l – заданное комплексное число, Tm(x) = tm×xm + … + t1×x + t0 – известный многочлен степени m. Правую часть вида ln×Tm(n), участвующую в этом соотношении,будем называть специальной. Теорема (о частном решении линейного неоднородного рекуррентного соотношения второго порядка с постоянными коэффициентами и специальной правой частью). Для любого неоднородного линейного рекуррентного соотношения с постоянными коэффициентами вида f(n+2) = a1×f(n+1) + a2×f(n) + ln×Tm(n), где l Î C , Tm(x) = tm×xm + … + t1×x + t0 – многочлен степени m, существует частное решение вида v(n) = ln×nr×Sm(n), где r – кратность корня l в характеристическом уравнении c(x) = x2 – a1×x – a2 (т.е. r = 0, если l – не корень, r = 1, если l – один из двух различных корней, r = 2, если l – единственный двукратный корень характеристического уравнения), Sm(x) – некоторый многочлен степени не выше m: Sm(x) = sm×xm + … + s1×x + s0 . Доказательство. Положим v(n) = ln×nr×(sm×nm + … + s1×n + s0) и подберём числа sm , … , s0 так, чтобы получилось решение данного рекуррентного соотношения. v(n + 2) – a1×v(n + 1) – a2×v(n) = ln×(tm×nm + … + t1×n + t0) Û Û ln+2×(sm×(n+2)m+r+sm–1×(n+2)m+r–1+…+s1×(n+2)1+r+s0×(n+2)r) – – a1×ln+1×( sm×(n+1)m+r+sm–1×(n+1)m+r–1+…+s1×(n+1)1+r+s0×(n+1)r) + + a2×ln×( sm×nm+r+sm–1×nm+r–1+…+s1×n1+r+s0×nr) = = ln×(tm×nm + … + t1×n + t0) Û {: ln ¹ 0} Û Û l2×(sm×(n+2)m+r+sm–1×(n+2)m+r–1+…+s1×(n+2)1+r+s0×(n+2)r) – – a1×l×( sm×(n+1)m+r+sm–1×(n+1)m+r–1+…+s1×(n+1)1+r+s0×(n+1)r) + + a2×( sm×nm+r+sm–1×nm+r–1+…+s1×n1+r+s0×nr) = = tm×nm + … + t1×n + t0 Û Û sm×[l2×(n+2)m+r – a1×l×(n+1)m+r – a2×nm+r] + … … + si×[l2×(n+2)i+r – a1×l×(n+1)i+r – a2×ni+r] + … … + s0×[l2×(n+2)r – a1×l×(n+1)r – a2×nr] = = tm×nm + … + t1×n + t0 . Рассмотрим три возможные случая, обозначенные в теореме: 1. l – не корень характеристического уравнения. Тогда r = 0, и последнее соотношение приобретает следующий вид: sm×[l2×(n+2)m – a1×l×(n+1)m – a2×nm] + … … + si×[l2×(n+2)i – a1×l×(n+1)i – a2×ni] + … … + s0×[l2×(n+2)0 – a1×l×(n+1)0 – a2×n0] = = tm×nm + … + t1×n + t0 Û {бином Ньютона} Û Û sm×[l2×(nm+ … + si×[l2×(ni+ … + s0×[l2 – a1×l – a2] = tm×nm + … + t1×n + t0 Û Û sm×[(l2–a1×l–a2)×nm +(l2× … + si×[(l2–a1×l–a2)×ni +(l2× …+ s0×[l2 – a1×l – a2] = tm×nm + … + t1×n + t0 . Для определения чисел s0 , s1 , … , sm приравняем коэффициенты при одинаковых степенях n, получив систему уравнений:
из которой последовательно и однозначно находятся все числа sm , sm–1 , … , s0 . 2. l = l1 ¹ l2 – простой корень характеристического уравнения. Тогда r = 1, и исследуемое соотношение приобретает следующий вид: sm×[l2×(n+2)m+1 – a1×l×(n+1)m+1 – a2×nm+1] + … … + si×[l2×(n+2)i+1 – a1×l×(n+1)i+1 – a2×ni+1] + … … + s0×[l2×(n+2)1 – a1×l×(n+1)1 – a2×n1] = = tm×nm + … + t1×n + t0 Û {бином Ньютона} Û Û sm×[l2×(nm+1+ … + si×[l2×(ni+1+ … + s0×[l2×(n+2) – a1×l×(n+1) – a2×n] = = tm×nm + … + t1×n + t0 Û Û sm×[(l2 – a1×l – a2)×nm+1+ …+si×[(l2 – a1×l– a2)×ni+1+ … + s0×[(l2 – a1×l – a2)×n + l2×2 – a1×l] = tm×nm + … + t1×n + t0 . Учитывая, что l2 – a1×l – a2 = 0 и приравнивая коэффициенты при одинаковых степенях n в левой и правой частях, получим
Здесь l2×2 – a1×l ¹ 0 поскольку l ¹ 0 (иначе a2 = 0) и l×2 – a1 ¹ 0 (иначе было бы l1 = l2).Поэтому из этой системы последовательно и однозначно находятся все числа sm , sm–1 , … , s0 . 3. l1 = l = l2 . Тогда r = 2, a1 = 2×l , a2 = l2 . Исследуемое соотношение в этом случае приобретает следующий вид: sm×[l2×(n+2)m+2 – a1×l×(n+1)m+2 – a2×nm+2] + … … + si×[l2×(n+2)i+2 – a1×l×(n+1)i+2 – a2×ni+2] + … … + s0×[l2×(n+2)2 – a1×l×(n+1)2 – a2×n2] = = tm×nm + … + t1×n + t0 t0 Û {бином Ньютона} Û Û sm×[l2×(nm+2+ … + si×[l2×(ni+2+ … + s0×[l2×(n2 +4×n + 4) – a1×l×(n2 + 2×n + 1) – a2×n2] = = tm×nm + … + t1×n + t0 Û Û sm×[(l2 – a1×l – a2)×nm+2+ …+si×[(l2 – a1×l– a2)×ni+2+ … + s0×[(l2 – a1×l – a2)×n2 + (l2×4 – a1×l×2)×n + l2×4 – a1×l] = tm×nm + … + t1×n + t0 . Учитывая, что l2 – a1×l – a2 = 0, a1 = 2×l и приравнивая коэффициенты при одинаковых степенях n в левой и правой частях, получим
Здесь l2×22 – a1×l ¹ 0 поскольку l ¹ 0 (иначе a2 = 0) и l×22 – a1 ¹ 0 поскольку a1 = 2×l. Поэтому из этой системы последовательно и однозначно находятся все числа sm , sm–1 , … , s0 . Теорема доказана. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 ×nm–1×2+…+
×nm–1×2+…+  ×n×2m–1+2m) – a1×l×(nm+
×n×2m–1+2m) – a1×l×(nm+  ×ni–1×2+…+
×ni–1×2+…+  ×n×2i–1+2i) – a1×l×(ni+
×n×2i–1+2i) – a1×l×(ni+ 
 +2m+1) – a1×l×(nm+1+
+2m+1) – a1×l×(nm+1+  +1) – a2×nm+1] + …
+1) – a2×nm+1] + …  +2i+1) – a1×l×(ni+1+
+2i+1) – a1×l×(ni+1+  +1) – a2×ni+1] +…
+1) – a2×ni+1] +…  + (l2×2m+1 – a1×l)] + …
+ (l2×2m+1 – a1×l)] + … + (l2×2i+1 – a1×l)] + …
+ (l2×2i+1 – a1×l)] + … .
. +2m+2) – a1×l×(nm+2+
+2m+2) – a1×l×(nm+2+  +1) – a2×nm+2] + …
+1) – a2×nm+2] + …  +2i+1) – a1×l×(ni+2+
+2i+1) – a1×l×(ni+2+  +1) – a2×ni+2] +…
+1) – a2×ni+2] +…  + (l2×2m+2 – a1×l)] + …
+ (l2×2m+2 – a1×l)] + … + (l2×2i+2 – a1×l)] + …
+ (l2×2i+2 – a1×l)] + …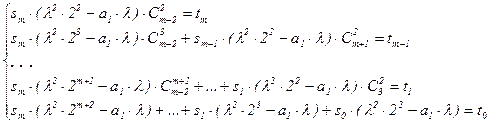 .
.