
|
|
Свойства функций, непрерывных на отрезке12 1) Все элем-ые ф-ции в области определения непрерывны. 2) Если f(x) непр-на в т. х0, то 3) Сумма, произвед-е и частное двух непр-ых ф-ций есть ф-ция непр-ая (делитель не равен нулю). 4) Пусть ф-ция u=φ(х) непр-на в точке х0, а функция у=ƒ(u) непр-вна в точке u0=φ(хо). Тогда сложная ф-ия ƒ(φ(х)), сост-я из непр-вных ф-ций, непр-на в точке х0. 5) Если ф-я у=ƒ(х) непрер. и строго монотонна на [a;b] оси Oх, то обр. ф-я у=φ(х) также непрер. и монотонна на соотв. отрезке [c;d] оси Оу. 42.Производная функции, ее геометр, механ, экон. Смысл. Эластичность функции. Пусть ф-ция y=f(x) определена на некот множ-тве Х, тогда произв.ф-цией y=f(x) назыв. предел отношения приращения ф-ции к приращению независ. переменной, если этот предел сущ-ет когда приращ-е аргумента стремится к нулю. Если ввести обозначения:
C геометр. точки зр. значения производной ф-ции, вычисленное в некот. точке т.е. f’( f’( Пусть задана ф-ция S=S(t), кот. опред-ет зависимость пути от времени,в механике S’(t)=V –мгнов.скорость в момент времени t. Пусть задана ф-ция у=f(x), для которой сущ-ет производная у’=f’(x). Эластич-тью ф-ции у=f(x) относ-но переменной х назыв-ся предел: Его обознач-т
Эластич-ть относ-но х есть приближен.процентн прирост ф-ции (повышение/пониж-е) при приращении независ переменной на 1%. 44. Основные правила дифференцирования. Таблица произв-ых. Операция нахождения производной назыв. дифференцированием. Пусть u=u(x), v=v(x)- некот диффер-мые ф-ии, с-конст. Тогда: 1)С’=0. 2)(u±v)’=u’±v’ 3)(uv)’=u’v+uv’. 4)(c u)’=c u’. 5)
Производная показательной функции: При
Производная неявной функции: При вычислении производной неявной функции воспользуемся правилом дифференцирования сложной функции. Продифференцируем уравнение
48. Производные высших порядков: Если f '(x) — производная функции f (x), то производная от нее по независимой переменной x, (f '(x))' = f ''(x), называется производной второго порядка. Аналогично определены производные 3-го, 4-го, , и т.д, n-го порядка: f''' (x) = ( f'' (x))' , f (4)(x) = (f''' (x))' , f (n)(x) = (f (n -1)(x))'
49. Теорема Ферма. Т-ма Ролля. Их геом смысл. Теорема Ферма: Пусть функция
Т. К. по усл. Теорема Роля: Пусть задана ф-ция Геом смысл теорем Роля и Ферма состо в том, что при выполн-и условий теоремы на инт-ле
50.Теорема Лагранжа о конечных приращениях, ее геометрический смысл. Теорема Лагранжа: Пусть задана ф-я
Она удовл-т всем условиям теоремы Ролля. Действительно, F(x) опред-на и непрер на
Тогда 51. Правило Лопиталя раскрытия неопределенностей.Пусть ф-и f(x) и g(x) одновр явл либо бескон б-ми, либо беск-но малыми в т.
39) Достаточное усл-е возраст-я (убыв-я) ф-й. Ф-я

12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
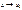 limf(x)= f(x0).
limf(x)= f(x0).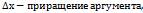
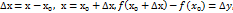 то выраж-е можно записать в виде:
то выраж-е можно записать в виде: Обозначается произ-я у’, f’(x),
Обозначается произ-я у’, f’(x), 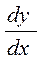 ,
,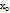 численно равно угловому коофициенту касательной, проведенной к графику ф-ции у=f(x) в точке с абсциссой
численно равно угловому коофициенту касательной, проведенной к графику ф-ции у=f(x) в точке с абсциссой 
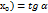
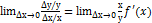
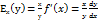
 6)y=f(u), где u=
6)y=f(u), где u= 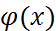 .Произв-я сложн ф-ции = произвед-ю произв-ых составляющих ее ф-ций: y’=
.Произв-я сложн ф-ции = произвед-ю произв-ых составляющих ее ф-ций: y’=  . Т-ца осн. пр-ых: (1/x)’=-1/
. Т-ца осн. пр-ых: (1/x)’=-1/ 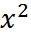 ;
;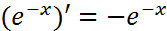 ;
;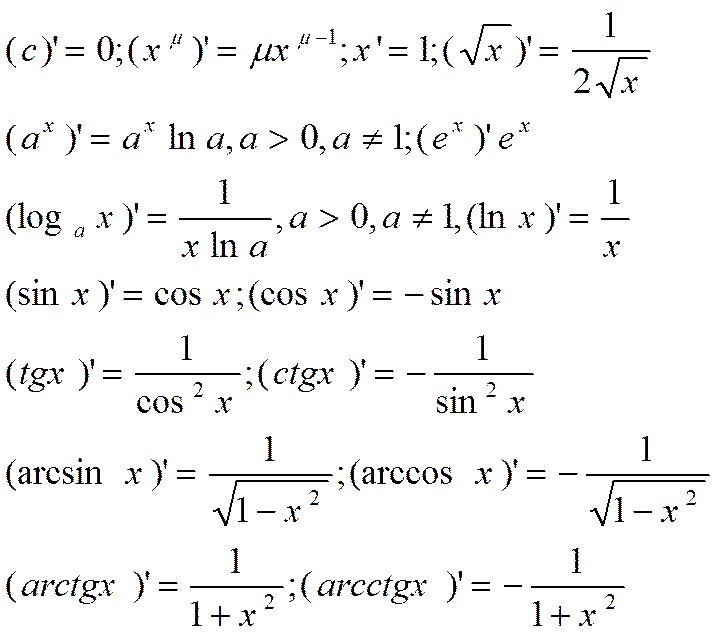
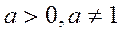 для любого х
для любого х
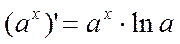
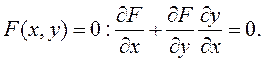 . Отсюда получим формулу для производной функции
. Отсюда получим формулу для производной функции 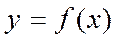 , заданной неявно:
, заданной неявно:  =
=  . Таким же способом нетрудно получить формулы для частных производных функции нескольких переменных, заданной неявно, например, уравнением
. Таким же способом нетрудно получить формулы для частных производных функции нескольких переменных, заданной неявно, например, уравнением 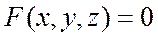 :
: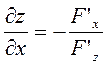 ,
, 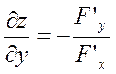 .
. определена на X и во внутренней точке С этого промежутка принимает наиб-е или наимен-е знач-е. Если сущ конечная пр-я
определена на X и во внутренней точке С этого промежутка принимает наиб-е или наимен-е знач-е. Если сущ конечная пр-я  , то необх-мо, чтобы
, то необх-мо, чтобы 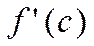
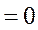 .Док-во: Пусть
.Док-во: Пусть 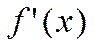 в точке с принимает наиб-е значение, т.е.
в точке с принимает наиб-е значение, т.е. 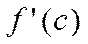 ≥
≥  для х
для х 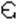 Х. По опред-ю пр-ой:
Х. По опред-ю пр-ой: 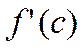 =
=  Этот предел не зависит от того, приближ-ся х к с слева или справа.Разность
Этот предел не зависит от того, приближ-ся х к с слева или справа.Разность 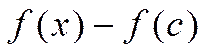 ≤0, следовательно, при х>с
≤0, следовательно, при х>с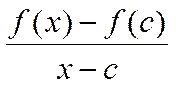 ≤0,а при x>c
≤0,а при x>c 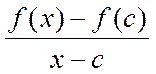 ≥0. Переходим к пределу:
≥0. Переходим к пределу: 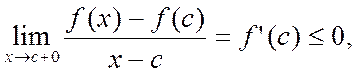
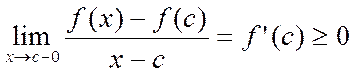
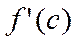 существует, то односторонние производные равны и
существует, то односторонние производные равны и 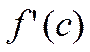 =0 ∆
=0 ∆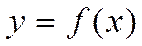 и пусть она: 1) определена и непрepывна на
и пусть она: 1) определена и непрepывна на 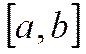 ; 2) дифференц-ма, по крайней мере, на
; 2) дифференц-ма, по крайней мере, на  ; 3) имеет равные значения на концах отрезка, т.е.
; 3) имеет равные значения на концах отрезка, т.е.  . Тогда найдётся с (a<c<b) такое, что
. Тогда найдётся с (a<c<b) такое, что  =0.Док-во: Ф-ция
=0.Док-во: Ф-ция 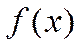 непрерывна на
непрерывна на 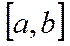 , следов-но, достиг наиб-го М и наимен-го m знач-й, т.е. m≤
, следов-но, достиг наиб-го М и наимен-го m знач-й, т.е. m≤ 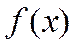 ≤M. Рассмотрим 2 случая:1)M=m. Тогда
≤M. Рассмотрим 2 случая:1)M=m. Тогда 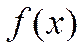 =const,
=const, 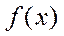 =М,
=М, 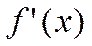 =0 и любую точку из
=0 и любую точку из 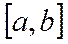 можно принять за с.2)M>m. Так как
можно принять за с.2)M>m. Так как 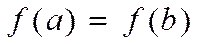 ,то М и m не достиг-ся оба на концах отрезка, т.е. хотя бы одно достиг-ся в точке c
,то М и m не достиг-ся оба на концах отрезка, т.е. хотя бы одно достиг-ся в точке c 
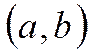 , а по теореме Ферма
, а по теореме Ферма 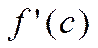 =0 ∆.
=0 ∆. 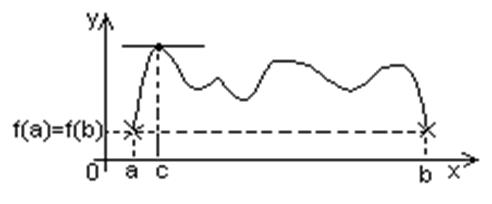
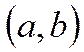 сущ точка e такая, что в соответ-ей т-ке кривой
сущ точка e такая, что в соответ-ей т-ке кривой 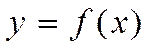 касательная ║ оси Ох. Таких точек на интервале может быть и неск-ко, но теорема утверждает существ-е по кр. мере 1 такой точки.
касательная ║ оси Ох. Таких точек на интервале может быть и неск-ко, но теорема утверждает существ-е по кр. мере 1 такой точки.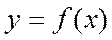 и пусть она: 1) опр-на и непрер на
и пусть она: 1) опр-на и непрер на 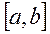 ; 2) имеет кон произв-ю
; 2) имеет кон произв-ю 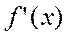 на
на 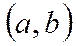 . Тогда найдётся такая т. с (a<c<b), что вып-ся рав-во
. Тогда найдётся такая т. с (a<c<b), что вып-ся рав-во Док-во: Введём вспомогат функцию
Док-во: Введём вспомогат функцию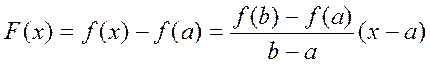
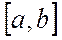 ,
, 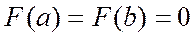 ,
, ,т.е. сущ на
,т.е. сущ на  . След-но, найдётся точка с (a<c<b), такая, что F’(c) = 0, т.е.
. След-но, найдётся точка с (a<c<b), такая, что F’(c) = 0, т.е. или
или 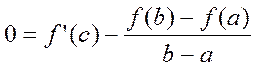
 ∆
∆ . Тогда при выч-и пределов
. Тогда при выч-и пределов 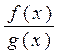 при x →
при x → 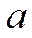 для раскрытия неопред-тей вида
для раскрытия неопред-тей вида  или
или  удобно применить пр. Лопиталя :
удобно применить пр. Лопиталя : ,
,  Неопределенности вида 0 · ∞, ∞ – ∞,
Неопределенности вида 0 · ∞, ∞ – ∞, 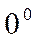 ,
, 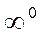 ,
, 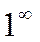 часто удается свести к неопределенностям вида
часто удается свести к неопределенностям вида 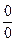 или
или 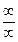 с помощью различных преобразований.
с помощью различных преобразований.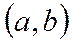 , если для любых
, если для любых 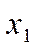 и
и 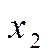 из этого инт-ла, для которых
из этого инт-ла, для которых 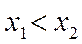 , верно нерав-во
, верно нерав-во 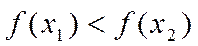 . Ф-я
. Ф-я 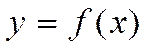 наз-ся убыв-ей на инт-ле
наз-ся убыв-ей на инт-ле 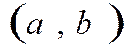 , если для любых x1 и x2 из этого инт-ла, для кот
, если для любых x1 и x2 из этого инт-ла, для кот  , верно нерав-во
, верно нерав-во  .Необх-ое усл-е возраст-я ф-ии:если ф-ия
.Необх-ое усл-е возраст-я ф-ии:если ф-ия  диффер-ма и возраста на инт-ле
диффер-ма и возраста на инт-ле 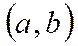 , то
, то 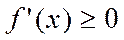 для всех х из этого инт-ла.Необх-ое усл-е убыв-я ф-ции. Если ф-ция
для всех х из этого инт-ла.Необх-ое усл-е убыв-я ф-ции. Если ф-ция  дифф-ма и убыва на инт-ле
дифф-ма и убыва на инт-ле  , то
, то  для всех х из этого инт-ла.Достаточное усл-е возраст-я (убыв-я ф-и). Пусть ф-я
для всех х из этого инт-ла.Достаточное усл-е возраст-я (убыв-я ф-и). Пусть ф-я 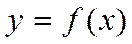 диф-ма на инт-ле
диф-ма на инт-ле  . Если во всех точках этого инт-ла
. Если во всех точках этого инт-ла 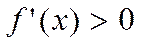 , то ф-ия возраста на этом интле, а если
, то ф-ия возраста на этом интле, а если  , то ф-я убывает на этом инт-ле.
, то ф-я убывает на этом инт-ле.