
|
|
Свойства линейной зависимости.1. Система из одного вектора линейно зависима тогда и только тогда, когда это нулевой вектор. 2. Система, содержащая более одного вектора, линейно зависима тогда и только тогда, когда среди данных векторов имеется такой, который выражается линейно через остальные. 3. Если часть системы векторов линейно зависима, то и вся система векторов линейно зависима. Таким образом, система, содержащая нулевой вектор, линейно зависима. 4. Если система векторов Рассмотрим систему векторов.
числа Любая лестничная система векторов линейно независимая. Определение 5: Векторы
Теорема: Любая система из S векторов
8.3 Базис арифметического пространства Rn. Ранее в 8.1 мы определяли понятие ортогональности для двух векторов из арифметического пространства Rn. В трёхмерном пространстве R3 для любых векторов Теорема 1: Пусть в арифметическом пространстве Rn задан набор из S векторов Дадим теперь одно из основных понятий арифметического пространства понятие базиса. Определение 1: Система векторов из арифметического пространства Rn, называется базисом пространства Rn, если: 1. Эти векторы линейно независимы. 2. Любой вектор из пространства Rn является линейной комбинацией векторов данной системы. Приведём пример базиса в пространстве Rn системы из n векторов:
Очевидно в силу того, что векторы
то есть вектор Следующая теорема формулирует еще одно очень важное свойство базиса. Теорема 2: Линейно независимая система векторов в пространстве Rn является базисом тогда и только тогда, когда число этих векторов равно n. Теперь рассмотрим примеры, посвящённые теме главы 8.
Пример 1: Вычислить скалярное произведение векторов
Решение: Для нахождения скалярного произведения векторов
тогда скалярное произведение равно.
Пример 2: При каком значении t будут перпендикулярны векторы Решение: Найдём проекции вектора
так как по условию задачи векторы
получим соотношение
Пример 3: Дана система из четырёх векторов в параметрическом пространстве R5
Установить является ли эта система векторов линейно зависимой. Из определения линейной зависимости вытекает векторное равенство для системы из четырёх векторов.
Перепишем это уравнение в координатной форме:
Получаем однородную систему уравнений если эта система имеет только нулевое решение, то ось заданных векторов линейно независима. Если же имеются ненулевые решения системы, то заданная система векторов линейно зависимая. Решим систему методом Жордана Гаусса. Для этого запишем размерную матрицу системы, дополнив ее столбцом контрольных сумм и столбцом базисных неизвестных. КΣ
В результате преобразований получили систему с тремя базисными неизвестными х1, х2, х4 и один свободный х3. наличие свободного неизвестного, говорит о том что система имеет бесконечное множество решений, а это значит что система векторов линейно зависима. Опишем линейное преобразование расширенной матрицы, проделанные при преобразовании матрицы. 1. Первую строку матрицы умножим на (-1). 2. В качестве разрешающего элемента выбрали элемент первой строки стоящий в первом столбце. Для получения нулей в первом столбце матрицы выполним следующие действия: a. Первую строку умножим на (-3) с сложим со второй строкой, результат запишем на место второй строки. b. Первую строку умножили на (-3) и сложили с третьей строкой результат записали на место третьей строки. c. Первую строку умножили на (-2) и сложили с четвёртой, результат записали в четвёртую строку. d. Первую строку умножили на (-5) и результат записали в пятую строку. 3. Вторую строку поделили на (-4); третью строку поделили на (-7); четвёртую строку поделили на (-3). 4. В качестве разрешающего элемента выбираем элемент второй строки стоящей во втором столбце. Для получения нулей во втором столбце матрицы выполним следующие действия: a. Вторую строку умножим на (-3) и сложим с первой строкой результат записываем на место первой строки. b. Вторую строку умножили на (-1) и сложили с третьей строкой, результат записали на место третьей строки. c. Вторую строку умножили на (-1) и сложили с четвёртой строкой результат записали на место четвёртой строки. d. Вторую строку умножили на (-11) и сложили с пятой строкой, записали на место пятой строки. 5. В матрице появились две нулевые строки третья и четвёртая, их вычёркиваем. 6. Третью строку делим на 2. 7. В качестве разрешающего элемента выбрали элемент третьей строки, стоящий в четвёртом столбце. Для получения нулей в четвертом столбце выполним действия: a. Третью строку умножим на (-2) и сложим со второй строкой, результат записали на место второй строки. b. Третью строку сложили с первой строкой результат записали на место первой строки.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 линейно независима, но при добавлении к ней ещё одного вектора
линейно независима, но при добавлении к ней ещё одного вектора  становится линейно зависимой, то вектор
становится линейно зависимой, то вектор 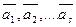

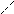


 стоящие на диагонали отличны от нуля. Такая система векторов называется лестничной, причём число векторов в лестничной системе не превосходит n.
стоящие на диагонали отличны от нуля. Такая система векторов называется лестничной, причём число векторов в лестничной системе не превосходит n. и
и  из арифметического пространства Rn называются коллинеарными если
из арифметического пространства Rn называются коллинеарными если 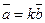 или
или 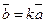 , в координатной форме:
, в координатной форме:
 в арифметическом пространстве Rn линейно зависима, если S>n.
в арифметическом пространстве Rn линейно зависима, если S>n. и
и  существует ненулевой вектор в виде теоремы на случай арифметического пространства Rn.
существует ненулевой вектор в виде теоремы на случай арифметического пространства Rn. причём S<n , тогда существует ненулевой вектор
причём S<n , тогда существует ненулевой вектор 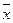 ортогональный каждому из векторов
ортогональный каждому из векторов 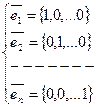
 образуют лестничную систему векторов они линейно независимы и если вектор
образуют лестничную систему векторов они линейно независимы и если вектор 
 и
и  , если заданы проекции векторов
, если заданы проекции векторов  в арифметическом пространстве Rs.
в арифметическом пространстве Rs.
 и
и 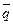 найдём их проекции в арифметическом пространстве Rs.
найдём их проекции в арифметическом пространстве Rs.


 , где векторы
, где векторы  и
и 






