Условия параллельности и перпендикулярности двух прямых

Пусть заданы прямые l₁ и l₂. своими общими уравненими; = (А₁,B₁), = (А₂,В₂) – нормальные векторы этих прямых; k₁ = tgα₁, k₂ = tgα₂ – угловые коэффициенты; = (m₁,n₁), (m₂,n₂) – направляющие векторы. Тогда, прямые l₁ и l₂ параллельны, в том и только том случае, если выполняется одно из следующих условий:

либо , либо k₁=k₂, либо .

Пусть теперь прямые l₁ и l₂ перпендикулярны. Тогда, очевидно, , то есть А₁А₂ + В₁В₂ = 0.

Если прямые l₁ и l₂ заданы соответственно уравнениями

l₁: у=k₁x + b₁,

l₂: у=k₂x + b₂,

то tgα₂ = tg(90º+α) = .

Отсюда следует, что

Наконец, если и направляющие векторы прямых, то ^ , то есть

m₁m₂ + n₁n₂ = 0

Последнее соотношение выражает необходимое и достаточное условие перпендикулярности двух прямых.

Угол между двумя прямыми

Под углом φ между двумя прямыми l₁ и l₂ будем понимать наименьший угол, на который надо повернуть одну прямую, чтобы она стала параллельной другой прямой или совпала с ней, то есть 0 £ φ £

Пусть прямые заданы общими уравнениями. Очевидно, что

cosφ=

Пусть теперь прямые l₁ и l₂ задана уравнениями с угловыми коэффициентами k₁ в k₂ соответственно. Тогда

Наконец, если и - направляющие вектора прямых, то

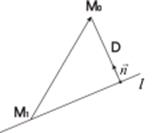
Расстояние от точки до прямой

Пусть d - расстояние от точки М₀(x₀,у₀) до прямой l, заданной уравнением Ax + By + С=0.

Тогда

.

ПЛОСКОСТЬ

Общее уравнение плоскости

Пусть в прямоугольной системе координат OXYZ задана плоскость α, проходящая через точку М₀(х₀,у₀,z₀). Возьмем произвольную точку М(х,у,z) α и обозначим (А,В,C) – нормальный вектор плоскости α.

Очевидно, что , то есть (х-х₀) + В(у-у₀) + C(z-z₀) = 0

Раскроем скобки и обозначим D= -Аx₀ - Ву₀ - Cz₀. Получим

Ax + By + Сz + D = 0 (*)

- уравнение плоскости в общем виде или общее уравнение плоскости.

Теорема. Линейное уравнение (*) (A²+B²+C² ≠ 0) является уравнением плоскости и обратно, любое уравнение плоскости является линейным.

Пусть

1) D = 0, тогда плоскость проходит через начало координат.

2) А = 0, тогда плоскость параллельна оси ОХ

3) А = 0, В = 0, тогда плоскость параллельна плоскости OXY.

Пусть в уравнении все коэффициенты отличны от нуля.

Тогда

- уравнение плоскости в отрезках. Числа |а|, |b|, |с| указывают на величины отрезков, отсекаемых плоскостью на координатных осях.

Уравнение плоскости, проходящей через три заданные точки

Пусть точки А(x₁,y₁,z₁), B(x₂,y₂,z₂), C(x₃,y₃,z₃) принадлежат плоскости α.

Тогда

- уравнение плоскости, проходящей через три заданные точки.

Нормальное уравнение плоскости

Пусть задана плоскость α и пусть - единичный, вектор нормали к плоскости α проведенный из начала координат. Обозначим р - расстояние от начала координат до плоскости α.

Для любой точки М(х,у,z) α

=p

Так как = (х,у,z),

= (cosα, cosβ, cosγ), где α, β, γ – углы, образованные вектором соответственно с осями OX, OY и 0Z, то отсюда получаем

xcosα + ycosβ + zсозγ – p = 0

– нормальное равнение плоскости.

Расстояние от точки до плоскости

Обозначим через d расстояние от точки M₀(x₀,y₀,z₀) до плоскости α, заданной общим уравнением вида (*).

Тогда

Взаимное расположение двух плоскостей

Пусть плоскости α₁ и α₂ заданы уравнениями:

α₁: А₁х + B₁y + C₁z + D₁ = 0,

α₂: А₂х + В₂y + С₂z + D₂ = 0.

Теорема. Тогда и только тогда плоскости α₁ и α₂:

1) совпадают, когда А₁=λA₂, B₁=λB₂, C₁=λC₂, D₁=λD₂;

2) параллельны и различны, когда A₁=λA₂, В₁=λВ₂, С₁=λС₂, D₁ λD₂;

3)пересекаются, когда коэффициенты А₁, В₁, С₁ не пропорциональны коэффициентам А₂, В₂, С₂

Пучок и связка плоскостей

Пучком плоскостей называется множество всех плоскостей, проходящих через некоторую прямую, называемую осью пучка.

Пусть в системе координат ОХУZ заданы две пересекающиеся плоскости α₁ и α₂ .

Тогда уравнение пучка имеет вид

А₁х + B₁y + C₁z + D₁ + λ(A₂x + B₂y + C₂z + D₂) = 0, где λ R.

Связкой плоскостей называется множество всех плоскостей, проходящих через некоторую точку, называемую центром связки. Если S₀ (x₀,y₀,z₀) – центр связки, то уравнение связки с центром в точке S₀ имеет вид

А(х-x₀) + В(у-y₀) + С(z­­-z₀) = 0,

где А, В и С – произвольные действительные числа, одновременно не равные нулю.

Угол между двумя плоскостями

Пусть даны плоскости α₁ и α₂ своими общими уравнениями. Тогда под углом φ между плоскостями α₁ и α₂ понимают наименьший угол, на который надо повернуть одну из плоскостей до ее совпадения с другой плоскостью. Поэтому . Очевидно, что либо φ=( ^, ), либо φ= (- ^, ), где и - нормальные векторы плоскостей α₁ и α₂ соответственно. В любом случае

В частности, если φ = π/2, то

А₁A₂ + В₁B₂ + С₁C₂ = 0

- условие перпендикулярности двух плоскостей.

ПРЯМАЯ В ПРОСТРАНСТВЕ.

ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМОЙ И ПЛОСКОСТИ В ПРОСТРАНСТВЕ

Не нашли, что искали? Воспользуйтесь поиском по сайту: