
|
|
Координаты в пространстве.
Определение. Пусть в пространстве заданы три координатные оси OX, OY и OZ с некомпланарными ортами Точка 0 - начало координат, векторы Так как векторы любого вектора
Числа x, y, z называются координатами точки М (записывается: М (х,у,z)), Афинную систему часто обозначают через OXYZ. Оси OX, OY, OZ называют соответственно осями абсцисс, ординат и аппликат. Плоскости, определяемые координатными осями, т.е. OXY, OYZ, OXZ, называют координатными плоскостями. Эти плоскости делят все пространство на восемь частей, называемых координатными октантами. Если упорядоченная тройка векторов В частности, если даны точки А (х1,у1,z1), В (х2,у2,z2), то
Векторы
Скалярное произведение векторов в координатной форме.
Пусть в прямоугольной системе координат заданы векторы:
В частности
Если даны точки А(х1,у1,z1) и В(х2,у2,z2), то, как известно,
-формула расстояния между двумя точками.
Так как
и
х1x2 + y1y2 + z1z2 = 0.
Определители второго и третьего порядков
Определение. Таблица, составленная из чисел, записанных в следующем виде:
называется квадратной матрицей n-го порядка или просто матрицей n-го порядка. Первый индекс i элемента аij матрицы А указывает на номер строки, а второй индекс j - на номер столбца, на пересечении которых стоит элемент аij.
Пусть дана квадратная матрица А второго порядка:
Определителем (детерминантом) матрицы А второго порядка называется число Δ равное:
Для матрицы А третьего порядка, где
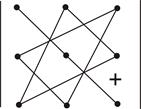
ее определитель Δ есть число, которое вычисляется следующим образом: Δ = а11а22а33 + а12а23а31 + а13а21а32 – а13а22а31 – а11а23а32 – а12а21а33.
Чтобы запомнить, какие произведения в правой части равенства берутся со знаком "+", а какие со знаком "–", полезно использовать следующее правило треугольников:
Легко проверить, что
- разложение определителя по элементам первой строки.
Векторное произведение векторов в координатной форме.
Пусть в прямоугольной системе координат заданы векторы
Последнее равенство можно записать так:
Итак,
Тогда
Смешанное произведение векторов в координатной форме.
Пусть в прямоугольной системе координат заданы векторы
Отсюда следует, что векторы
Полярные координаты.
Возьмем на плоскости произвольную точку 0, которую назовем полюсом, и ось ОР, задаваемую единичным вектором Величины r и φ называются полярными координатами точки М, r-полярный радиус, φ-полярный угол. При этом считаем, что полярные координаты точек плоскости изменяются в следующих пределах: С прямоугольными координатами полярные связаны следующими соотношениями: х = r cosφ, у = r sinφ.
Так как х2 + у2 = r2, то

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
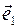 ,
,  ,
, 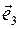 соответственно. Тогда четверка (0,
соответственно. Тогда четверка (0,  имеет место разложение:
имеет место разложение: называется радиус-вектором точки М с координатами х, у, z (записывается:
называется радиус-вектором точки М с координатами х, у, z (записывается:  .
.
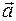 = (х1,у1,z1) и
= (х1,у1,z1) и  = (х2,у2,z2) коллинеарны тогда и только тогда, когда их соответствующие координаты пропорциональны, т.е.
= (х2,у2,z2) коллинеарны тогда и только тогда, когда их соответствующие координаты пропорциональны, т.е.
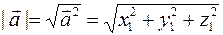
 =(x2-х1,y2-у1,z2-z1) и значит.
=(x2-х1,y2-у1,z2-z1) и значит.
 , то
, то
 тогда и только тогда, когда выполняется равенство:
тогда и только тогда, когда выполняется равенство:
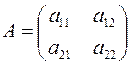



 =
= 




 = (x3,y3,z3). Тогда
= (x3,y3,z3). Тогда


 , которую назовем полярной осью. Тогда положение произвольной точки М плоскости можно определить двумя числами: r -длина отрезка ОМ и φ - угол, который образует отрезок ОМ с осью ОР в положительном направлении, т.е. при движении против часовой стрелки.
, которую назовем полярной осью. Тогда положение произвольной точки М плоскости можно определить двумя числами: r -длина отрезка ОМ и φ - угол, который образует отрезок ОМ с осью ОР в положительном направлении, т.е. при движении против часовой стрелки. . Таким образом, получаем систему координат, которая называется полярной системой координат.
. Таким образом, получаем систему координат, которая называется полярной системой координат.