
|
|
Умножение вектора на число.Опр. 10. Произведением вектора имеющий длину ka, и направление, которого: 1. совпадает с направлением вектора 2. противоположно направлению вектора 3. произвольно, если k = 0. Свойства умножения вектора на число. 1о. (k + l) k( 2o. k(l 3o. 1× Свойства векторов. Опр. 11.Два вектора Нулевой вектор Теорема 1. Два ненулевых вектора Опр. 12. Три вектора Теорема 2. Три ненулевых вектора Проекция вектора на ось. Теорема 3.Проекция вектора
рис.3. КООРДИНАТЫ ВЕКТОРА Опр. 13. Проекции вектора Длина вектора: Пример:Вычислить длину вектора Решение: Расстояние между точками Пример:Найти расстояние между точками М (2,3,-1) и К (4,5,2). Действия над векторами в координатной форме. Даны векторы 1. ( 2. l Скалярное произведение векторов. Определение:Под скалярным произведением двух векторов понимается число, равное произведению длин этих векторов на косинус угла между ними, т.е. Свойства скалярного произведения: 1. 2. ( 3. 4. 5. 6. два вектора перпендикулярны (ортогональны), если 7. Скалярное произведение в координатной форме имеет вид: Пример:Найти скалярное произведение векторов Решение: Векторное проведение векторов. Определение: Под векторным произведением двух векторов -модуль равен площади параллелограмма, построенного на данных векторах, т.е. -этот вектор перпендикулярен перемножаемым векторам, т.е. -если векторы Свойства векторного произведения: 1.При изменении порядка сомножителей векторное произведение меняет свой знак на обратный, сохраняя модуль, т.е. 2.Векторный квадрат равен нуль-вектору, т.е. 3.Скалярный множитель можно выносить за знак векторного произведения, т.е. 4.Для любых трех векторов 5.Необходимое и достаточное условие коллинеарности двух векторов Векторное произведение в координатной форме. Если известны координаты векторов Тогда из определения векторного произведения следует, что площадь параллелограмма, построенного на векторах Пример:Вычислить площадь треугольника с вершинами Решение: Смешанное произведение векторов. Определение:Смешанным (векторно-скалярным) произведением векторов Свойства смешанного произведения: 1.Смешанное произведение не меняется при циклической перестановке его сомножителей, т.е. 2.При перестановке двух соседних сомножителей смешанное произведение меняет свой знак на противоположный, т.е. 3.Необходимое и достаточное условие компланарности трех векторов 4.Смешанное произведение трех векторов равно объему параллелепипеда, построенного на этих векторах, взятому со знаком плюс, если эти векторы образуют правую тройку, и со знаком минус, если они образуют левую тройку, т.е. Если известны координаты векторов Пример:Вычислить смешанное произведение векторов Решение: Базис системы векторов. Определение.Под системой векторов понимают несколько векторов, принадлежащих одному и тому же пространству R. Замечание. Если система состоит из конечного числа векторов, то их обозначают одной и той же буквой с разными индексами. Пример. Определение. Любой вектор вида Пример. Определение. Если вектор Определение. Система векторов называется линейно-независимой, если ни один вектор системы не может быть как линейная комбинация остальных векторов. В противном случае систему называют линейно-зависимой. Пример. Система векторов Определение базиса.Система векторов образует базис, если: 1) она линейно-независима, 2) любой вектор пространства через нее линейно выражается. Пример 1.Базис пространства 2. В системе векторов Замечание.Чтобы найти базис данной системы векторов необходимо: 1) записать координаты векторов в матрицу, 2) с помощью элементарных преобразований привести матрицу к треугольному виду, 3) ненулевые строки матрицы будут являться базисом системы, 4) количество векторов в базисе равно рангу матрицы. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
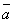 на скаляр k называется вектор
на скаляр k называется вектор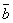 = k
= k  .
.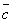 называются компланарными, если они параллельны некоторой плоскости или лежат в ней.
называются компланарными, если они параллельны некоторой плоскости или лежат в ней.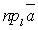 = a × cos a, a = Ð(
= a × cos a, a = Ð( 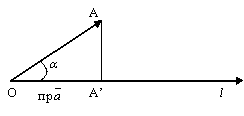
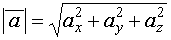


 .
.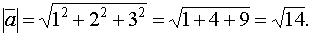
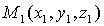 и
и  вычисляется по формуле:
вычисляется по формуле:  .
.
 и
и 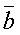
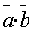 =
= 
 ,
, 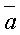 и
и  ×
× 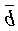 =
= 
 +
+ 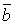 )
)  =
= 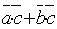
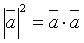
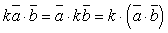
 , где
, где 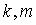 – скаляры.
– скаляры. .
. тогда и только тогда, когда
тогда и только тогда, когда 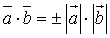 .
. ,где
,где 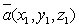 и
и  .
. и
и 

 и
и 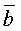 понимается вектор,
понимается вектор, 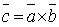 для которого:
для которого: , где
, где  угол между векторами
угол между векторами 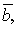

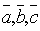 неколлинеарны, то они образуют правую тройку векторов.
неколлинеарны, то они образуют правую тройку векторов.
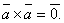
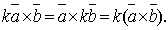
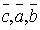 справедливо равенство
справедливо равенство 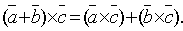
 и
и  :
: 
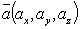 и
и  ,то их векторное произведение находится по формуле:
,то их векторное произведение находится по формуле:
 и
и  , вычисляется по формуле:
, вычисляется по формуле:
 (1;-1;2),
(1;-1;2),  (5;-6;2),
(5;-6;2),  (1;3;-1).
(1;3;-1). .
. ,
,  , тогда площадь треугольника АВС будет вычисляться следующим образом:
, тогда площадь треугольника АВС будет вычисляться следующим образом: ,
,
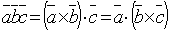 .
. .
.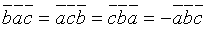 .
. =0.
=0.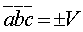 .
. ,то смешанное произведение находится по формуле:
,то смешанное произведение находится по формуле: 
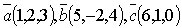 .
.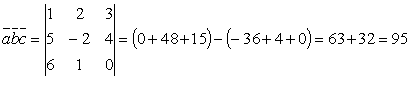
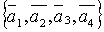
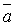 =
=  называется линейной комбинацией векторов
называется линейной комбинацией векторов  . Числа
. Числа 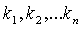 -коэффициентами линейной комбинации.
-коэффициентами линейной комбинации. .
.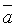 является линейной комбинацией векторов
является линейной комбинацией векторов  , то говорят, что вектор
, то говорят, что вектор  линейно выражается через векторы
линейно выражается через векторы  линейно-зависима, т. к. вектор
линейно-зависима, т. к. вектор 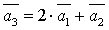 .
. :
:  .
. , т.к.
, т.к. 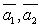 .
.