
|
|
Достоинства и недостатки метода Адамса12 Чтобы начать расчет методом Адамса, недостаточно знать Внешне этот метод привлекателен тем, что за один шаг приходится только один раз вычислять Поэтому сейчас метод Адамса и аналогичные методы (например, Милна) употребляются реже метода Рунге – Кутта.
Решение систем обыкновенных дифференциальных уравнений методом Адамса Метод Адамса применяется как для решения простых дифференциальных уравнений, так и для их систем.
Постановка задачи
Методом Адамса найти решение системы уравнений на отрезке
где
Решение систем обыкновенных дифференциальных уравнений методом Адамса
В данную систему уравнений подставим значения коэффициентов и начальные условия. Получим
адамс дифференциальный уравнение результат Методом Адамса найдем решение этой системы на заданном отрезке. Для этого вычислим методом Рунге-Кутта несколько начальных значений функции. Выберем шаг Рассмотрим числа:
Согласно методу Рунге-Кутта последовательные значения
где
Подставив в эти формулы начальные значения получим
Дальше вычисления продолжаем по методу Адамса. Все расчеты записываем в таблицах 2.1 и 2.2.
Таблица 2.1
Таблица 2.2
Полученные по формуле (1.3) значения необходимо уточнить, рассчитав их по формуле (1.4). Полученные данные запишем в таблицу.
Таблица 2.3
Решение систем обыкновенных дифференциальных уравнений точным методом
Для решения системы выразим
Находим производную функции
Подставим полученное значение по второе уравнение
Заменим это уравнение на параметрическое и решим его. Получим корни уравнения
Общее решение имеет вид
Учитывая начальные условия система принимает вид
Решив систему получим
Подставив полученные значения в общее решение системы получим
Сравнение результатов решения
Описание программы
Описание реализации пунктов алгоритма и руководство для пользователя Дана система дифференциальных уравнений с заданными начальными условиями и отрезок отделения корня. Перед началом работы в соответствующие поля на форме необходимо ввести недостающие коэффициенты и запустить программу. Программа начинает работу с расчета начальных значений функции по методу Рунге-Кутта и, подставив их в уравнения метода Адамса, производит последующие вычисления. После расчетов значений функции в соответствующих точках производиться уточнение полученных данных. В результате вычислений на форме программы появляются заполненные таблицы с расчетами
Блок-схема

12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 . Для начала расчета по формуле (1.3) надо знать величину решения в четырех точках
. Для начала расчета по формуле (1.3) надо знать величину решения в четырех точках  . Поэтому надо вычислить недостающие значения
. Поэтому надо вычислить недостающие значения  каким-либо другим методом, например методом Рунге – Кутта, или разложением по формуле Тейлора с достаточно большим числом членов. При работе на ЭВМ это вдвое увеличивает объем программы. Кроме того, формулы (1.3) громоздки, а несложные формулы (1.4) рассчитаны только на постоянный шаг и требуют нестандартных действий при смене шага: надо перейти к формулам (1.3), сделать по ним четыре шага и снова вернуться к формулам (1.4). Все это делает метод Адамса неудобным для расчетов на ЭВМ.
каким-либо другим методом, например методом Рунге – Кутта, или разложением по формуле Тейлора с достаточно большим числом членов. При работе на ЭВМ это вдвое увеличивает объем программы. Кроме того, формулы (1.3) громоздки, а несложные формулы (1.4) рассчитаны только на постоянный шаг и требуют нестандартных действий при смене шага: надо перейти к формулам (1.3), сделать по ним четыре шага и снова вернуться к формулам (1.4). Все это делает метод Адамса неудобным для расчетов на ЭВМ. , которая может быть очень сложной. А в четырехчленной схеме Рунге – Кутта того же порядка точности
, которая может быть очень сложной. А в четырехчленной схеме Рунге – Кутта того же порядка точности  с точностью
с точностью 


 – заданные константы
– заданные константы
 и, для краткости, введем
и, для краткости, введем  и
и 

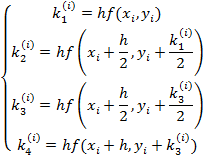
 определяются по формуле
определяются по формуле

 . (2.1)
. (2.1)




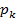











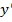
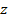



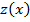 из первого уравнения
из первого уравнения .
. .
. .
.








