
|
|
ТЕОРИЯ К КОНТРОЛЬНОЙ РАБОТЕ № 66.1. Переменная величина z называется функцией двух переменных x и y, если каждой паре значений (x, y) (точке (x, y) плоскости D) поставлено в соответствие единственное значение z из множества вещественных (действительных) чисел. Функцию двух переменных записывают в виде
z = f(x, y).
Переменные x и y называются аргументами, т.е. независимыми переменными. Множество D называется областью определения функции двух переменных. Графиком функции z = f(x, y) является множество точек (x, y, f(x, y)), т.е. поверхность, уравнение которой
z = f(x, y).
6.2. Переменной x дадим приращение ∆х, а y оставим без изменения. Если существует предел
то он называется частной производной от функции z = f(x, y) по переменной x. Обозначать частную производную от функции z = f(x, y) по переменной x можно любым из символов
Чтобы найти частную производную от функции z = f(x, y) по переменной x, нужно найти производную от этой функции по x, считая, что y = const. Аналогично, частной производной от функции z = f(x, y) по переменной y называется предел
и обозначается одним из символов
Частная производная от функции z = f(x, y) по переменной y – это производная от функции z = f(x, y) по переменной y в предположении, что x = const. Частные производные от функции нескольких переменных находятся как производные от функции одной переменной при условии, что все остальные переменные считаются на момент дифференцирования постоянными.
6.3. Частными производными второго порядка от функции z = f(x, y) называются частные производные от частных производных первого порядка
Частные производные
6.4. Пусть А(х0; у0) – данная точка, а B(х0 + Δх; у0 + Δy) – близкая точка, отвечающая приращениям аргументов Δх и Δy. Полным приращением Δz функции z = f(x, y) в точке А(х0; у0) называется разность f(B) – f(A), т.е.
Δz = f(х0 + Δх, у0 + Δy) - f(х0, у0).
Если полное приращение Δz можно представить в виде
где ε – бесконечно малая более высокого порядка по сравнению с расстоянием Главная часть полного приращения функции z = f(x, y), линейная относительно Δх и Δу, называется полным дифференциалом функции в точке A и обозначается
6.5. Применение полного дифференциала кприближенным вычислениям. Полное приращение функции Δz и ее полный дифференциал связаны равенством Δz = dz + ε. При достаточно малых приращениях аргументов можно полное приращение функции Δz с малой относительной погрешностью заменить полным дифференциалом dz, т.е. Δz ≈dz или f(х0 + Δх, у0 + Δy) - f(х0, у0) ≈dz. Окончательно формула для приближенного вычисления с помощью полного дифференциала имеет вид f(х0 + Δх, у0 + Δy) = f(х0, у0) +dz. 6.5.1. Относительная погрешность δ, возникающая при замене приращения функции ее дифференциалом, вычисляется по формуле
где z1 = f(В) – точное значение функции в точке В; z2 = f(А) + dz – приближенное значение функции в точке В.
6.6. Касательная плоскость к поверхности z = f(x, y) в точке М0(х0; у0; z0), где z0 = f(x0, y0), задается уравнением
6.7. Нормаль к поверхности z = f(x, y) в точке М0(х0; у0; z0), т.е. прямая, проходящая через точку М0 перпендикулярно касательной плоскости, задается уравнениями
6.8. Если кривая задана как вектор-функция скалярного аргумента, т.е.
то вектор
направлен по касательной к этой кривой в точке М(x(t); y(t); z(t)).
6.8.1. Уравнение касательной к кривой
6.8.2. Плоскость, проходящая через точку М0(х0; у0; z0) перпендикулярно касательной (т.е. перпендикулярно вектору x/(t0)∙(x-x(t0)) + y/(t0)∙(у-у(t0)) + z/(t0)∙(z-z(t0)) = 0.
6.8.3. Если кривая задана уравнением то радиус кривизны кривой вычисляется по формуле где
вычисляются по формуле
Если известны координаты некоторого вектора то модуль этого вектора равен
6.9. Точка М0(х0; у0) называется точкой локального максимума (минимума) функции z = f(x, y), если для всех точек М(х; у), отличных от точки М0(х0; у0) и принадлежащих достаточно малой ее окрестности, выполняется неравенство f(x0, y0) > f(x, y) (f(x0, y0) < f(x, y) ). точки максимума и минимума функции называются точками экстремума этой функции. М0(х0; у0) Î области определения функции.
6.9.1. необходимые условия экстремума. Если точка М0(х0; у0) является точкой экстремума функции z = f(х, у), то
или хотя бы одна из этих частных производных не существует. точки, в которых частные производные первого порядка
называются стационарными. точки, найденные из необходимых условий экстремума, называются стационарными или критическими (если хотя бы одна из частных производных не существует). точки экстремума функции всегда являются стационарными (критическими) точками, но стационарная (критическая) точка может и не быть точкой экстремума.
6.9.2. Достаточные условия экстремума. Сначала введем обозначения Пусть М0(х0; у0) − критическая точка функции z = f(x, y). Тогда 1) если М0(х0; у0) будет точкой максимума при А < 0 (C < 0) и точкой минимума при А > 0 (C > 0); 2) если 3) если
6.10. Для того чтобы найти наибольшее и наименьшее значения функции z = f(x, y) в замкнутой ограниченной области D, следует 1) найти из условия стационарные точки функции z = f(x, y), лежащие внутри области D, и вычислить значения функции в них; 2) найти наибольшее и наименьшее значения функции z = f(x, y) на границе области D. Нахождение наибольшего и наименьшего значений функции z = f(x, y) на границе области D сведется к решению нескольких задач (по числу кривых, ограничивающих область D) на нахождение наибольшего и наименьшего значений функции одной переменной на отрезке [a, b]. Для этого в функцию z = f(x, y) подставить из уравнения границы выражение у через х (или х через у). Получим функцию одной переменной, заданной на некотором отрезке [a, b]; 3) из полученных в пунктах 1 и 2 значений выбрать наибольшее и наименьшее – это и будет ответ.
6.11. Градиентом функции z = f(x, y) называется вектор, проекциями которого на координатные оси являются соответствующие частные производные этой функции
координаты которого числа
6.12. производная функции z = f(x, y) по направлению l,заданномувектором
где направляющие косинусы
Замечание 1. производная функции z = f(x, y) в данном направлении характеризует скорость изменения функции z в этом направлении, причем, если Замечание 2. в направлении градиента функция возрастет с наибольшей скоростью, причем

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 ,
,




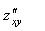 и
и  называются смешанными частными производными второго порядка. В точках, где смешанные производные непрерывны, они равны, т.е.
называются смешанными частными производными второго порядка. В точках, где смешанные производные непрерывны, они равны, т.е.

 между точками A и B (т.е.
между точками A и B (т.е.  при
при  ), то функция z = f(x, y) называется дифференцируемой в точке A. Точки A и B из области определения функции.
), то функция z = f(x, y) называется дифференцируемой в точке A. Точки A и B из области определения функции.



 ,
,
 , проходящей через точку, отвечающую значению t0, т.е. через точку М0(х0; у0; z0), где x0 = x(t0), y0 = y(t0), z0 = z(t0), имеет вид
, проходящей через точку, отвечающую значению t0, т.е. через точку М0(х0; у0; z0), где x0 = x(t0), y0 = y(t0), z0 = z(t0), имеет вид
 ), называется нормальной плоскостью к кривой
), называется нормальной плоскостью к кривой  в точке М0(х0; у0; z0). Уравнение нормальной плоскости имеет вид
в точке М0(х0; у0; z0). Уравнение нормальной плоскости имеет вид ,
,

 – векторное произведение вектора
– векторное произведение вектора  на вектор
на вектор  – это вектор, координаты которого
– это вектор, координаты которого

 ,
,
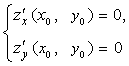

 ,
,  ,
,  ,
,  .
. , то точка М0(х0; у0) является точкой экстремума для функции, причем
, то точка М0(х0; у0) является точкой экстремума для функции, причем , то в точке М0(x0; y0) экстремума нет;
, то в точке М0(x0; y0) экстремума нет; , то в точке М0(x0, y0) экстремум может быть, а может и не быть (нужно дополнительное исследование), т.е. ответом будет «не знаем».
, то в точке М0(x0, y0) экстремум может быть, а может и не быть (нужно дополнительное исследование), т.е. ответом будет «не знаем».

 − вектор,
− вектор, .
. , вычисляется по формуле
, вычисляется по формуле


 , то функция убывает, если
, то функция убывает, если  , то функция возрастет в данном направлении.
, то функция возрастет в данном направлении.