
|
|
Взаимодействие элементов тока
Комбинируя определение магнитного поля (5) и закон Био – Савара (8), можно получить выражение для силы взаимодействия двух произвольно ориентированных элементов тока (аналогичное закону Кулона в электростатике). Выражение это оказывается, однако, довольно громоздким, ибо в него войдет двойное векторное произведение, которое заметно не упрощается. В то же время для анализа возникающих при таком взаимодействии нюансов нам достаточно рассмотреть его частный случай взаимно перпендикулярных элементов, один из которых лежит на оси другого (рис. 7). Поскольку элемент I1Dl1 находится на оси элемента I2Dl2 , последний не возбуждает поле в месте нахождения первого и, следовательно, элемент I1Dl1 никакой силы со стороны I2Dl2 испытывать не будет (F21 = 0). Элемент же I2Dl2, напротив, лежит в перпендикулярной к току I1Dl1 и пересекающей его плоскости, т. е. там, где его поле как раз максимально (sin a = 1). Индукция поля B12 этого тока направлена на рис. 7 от нас, и элемент 2 будет испытывать силу F12 , действующую вверх. Таким образом, F12 ¹ – F21 и налицо явное нарушение третьего закона Ньютона. В чем же здесь дело? Мы пришли к этому противоречию потому, что незаметно встали на точку зрения дальнодействия. Ведь перейдя к взаимодействию элементов друг с другом, мы исключили из рассмотрения весьма существенный физический объект – магнитное поле, а этого делать нельзя. В том, что третий закон Ньютона здесь не выполняется, ничего удивительного нет: ведь если рассматривать его в рамках дальнодействия (т. е. в формулировке, данной в § 2.3), то он в определенных ситуациях может и даже должен нарушаться. Рассмотренный пример этого нарушения является еще одной иллюстрацией[22] несостоятельности теории дальнодействия. Если же встать на точку зрения близкодействия и включить в рассмотрение возбуждаемое токами магнитное поле, то полученное противоречие может быть устранено. С точки зрения близкодействия элемент I2Dl2 взаимодействует не с элементом I1Dl1, а с его полем. «Ощущая» со стороны этого поля силу F12 , он, в свою очередь, образно говоря, сам «действует на него» с равной и противоположной силой «отдачи», что проявляется в изменении импульса поля[23]. Можно строго показать, что при любых взаимодействиях зарядов и токов полный (т. е. механический и электромагнитный) импульс замкнутой системы сохраняется. Поскольку закон сохранения импульса полностью эквивалентен третьему закону Ньютона (в его обобщенной форме, включая в рассмотрение поле), то этим и устраняется указанное противоречие. А если взаимодействуют два замкнутых постоянных тока? И электрическое, и магнитное поля таких токов стационарны, т. е. со временем не меняются. Не может измениться, следовательно, и электромагнитный импульс этого поля. Тем не менее, и в этом случае третий закон выполняется, только применять его надо уже не к отдельным элементам тока, а в целом к контурам. Ведь как уже отмечалось, в этом случае экспериментально невозможно из результирующего поля каждого контура выделить вклады отдельных его элементов, а потому опытной проверке подлежит лишь силовое воздействие на токи этого суммарного поля. Расчеты же показывают, что для двух произвольных контуров суммирование сил попарного взаимодействия их элементов (полученных из (5) и (8)) всегда дает результирующие силы, удовлетворяющие третьему закону Ньютона. Таким образом, отмеченное кажущееся противоречие не опровергает, а лишний раз подтверждает описанный нами механизм магнитного взаимодействия токов.
Контрольные вопросы и задания
1. Что называется векторным произведением векторов. Коммутативно ли оно? 2. Дать определение вектора индукции магнитного поля. Почему его определение через момент сил, действующих на рамку с током, не вполне корректно? 3. Дать название и определение единицы магнитного поля. 4. Сформулировать правило левой руки. 5. Можно ли в рамках магнитостатики экспериментально определить силу, испытываемую малым элементом постоянного тока? Если да, то как именно, если нет – почему? 6. Сформулировать закон Био – Савара. Как меняется поле малого элемента тока при удалении от него по разным направлениям точки наблюдения? Что представляет собой линия В элемента тока? 7. Можно ли в рамках магнитостатики экспериментально определить поле, созданное малым элементом постоянного тока? Если да, то как именно, если нет – почему? 8. Сформулировать принцип суперпозиции полей в магнитостатике. 9. Каким требованиям должен удовлетворять «пробный» элемент тока? 10. Найти поле в центре кругового тока. 11. Удовлетворяют ли третьему закону Ньютона силы взаимодействия двух элементов тока? Двух замкнутых постоянных токов? Лекция 17 Основные уравнения магнитостатики Для магнитного поля постоянных токов могут быть получены уравнения, аналогичные электростатическим (7л11). Уравнения эти выводятся из закона Био – Савара и принципа суперпозиции (и в свою очередь влекут за собой их выполнение). Поскольку, однако, закон Био – Савара существенно сложнее своего электростатического аналога, вывод уравнений магнитостатики выходит за пределы того математического аппарата, которым мы владеем. Нам под силу оказывается лишь доказательство одного из них, и то для частного случая прямых бесконечных токов. Теорема о циркуляции
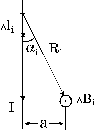
1. Поле прямого тока. Рассмотрим прямой бесконечный провод, несущий постоянный линейный ток I (рис. 1), и найдем поле B в произвольной точке M на расстоянии a от него. Для этого разобьем провод на малые элементы Dli << a, посчитаем вклад каждого из них и результаты просуммируем. В соответствии с законом Био – Савара поле DBi отрезка Dli изображенного на рис. 1, будет направлено перпендикулярно плоскости чертежа на нас, а величина его
где Ri – расстояние от Dli до исследуемой точки поля, а ai угол между Dli и Ri. По принципу суперпозиции полное поле B направлено в ту же сторону, а величина его
где суммирование производится по всем элементам, на которые разбит наш ток. Для вычисления входящей в (1) суммы рассмотрим аналогичную электростатическую задачу расчета поля бесконечной прямой нити (рис. 2) с равномерно распределенным по ней зарядом линейной плотности
где Dq – заряд, находящийся на отрезке нити длиной Dl. Поле DEi в произвольной точке M на расстоянии a от нити, создаваемое ее участком Dli , будет направлено (для определенности полагаем E = где Теперь понятно, для чего мы прибегли к электростатическому аналогу нашей задачи: в (2) входит та же сумма, что и в (1)! Но сейчас мы легко можем ее найти, ведь поле E без труда вычисляется с помощью теоремы Гаусса. Предоставляя эти вычисления провести читателю самостоятельно, напишем лишь их результат: E = Сравнивая (3) с (2), получаем
что после подстановки в (1) дает B = Заметим, что это соотношение используется для определения единицы силы тока – ампера, которая является одной из основных в системе СИ. Если два длинных прямолинейных проводника с текущими в одном направлении одинаковыми токами I расположить параллельно друг другу на расстоянии a, то между ними, как нетрудно видеть, возникнет сила притяжения, величина которой в расчете на участок проводника длины Dl F = IDlB = По определению I = 1 А, если при a = 1 м и Dl = 1 м, F = 2 × 10–7 Н, т. е. за единицу силы тока – ампер – принимается такой линейный ток, который действует на равный ему ток, расположенный на расстоянии 1 м, с силой 2. Циркуляция вектора B. Найдем сначала циркуляцию вектора B вдоль линии этого вектора, т. е. вычислим сумму
Докажем, что такой же[25] будет циркуляция B и при обходе по произвольной замкнутой кривой Г, лежащей в перпендикулярной току плоскости и охватывающей его (рис. 3). Для этого проведем из точки M, в которой ток пронизывает плоскость, два луча под небольшим углом Db друг к другу. Лучи эти вырежут малый (практически прямолинейный) отрезок Dl кривой Г, вклад которого в циркуляцию Bl Dl = BDl cos a = ± BDl¢, (5) где a – угол между векторами Dl и B, а Dl¢ – ограниченный нашими лучами отрезок линии B, проходящей через элемент Dl, причем в (5) нужно брать, очевидно, «+», если cos a > 0, и «–», если cos a < 0. Оба эти случая можно охватить одним выражением ± Dl¢ = aDb, если угол Db считать алгебраическим, т. е. положительным, когда cos a > 0, или проекция Dl на линию В положительна, и отрицательным, когда эта проекция меньше нуля. В первом случае, очевидно, направления Dl и тока образуют правовинтовую систему, во втором – левовинтовую. Таким образом, с учетом (4),
B1Dl = т. е. вклад отрезка Dl в циркуляцию не зависит от его расстояния до тока, а определяется, помимо величины I, лишь (положительным или отрицательным) углом Db, под которым виден этот отрезок из точки пересечения тока с плоскостью. Суммируя выражения типа (6) для всей замкнутой кривой Г, получим
где b – полный угол, под которым видна из М вся кривая Г. Если она не охватывает тока (рис. 4), то, очевидно, b = 0, ибо кривая эта разделится точками 1 и 2 на две части, дающие в циркуляцию противоположные вклады. Если же она охватывает ток один раз[26] (см. рис. 3), то b = ± 2p[27] (в зависимости от произвольно выбранного направления обхода Г) и
причем знак b можно приписать току I, считая его положительным, если он образует с направлением обхода Г правовинтовую систему, и отрицательным в противном случае. Поскольку по определению тока его знак связан с выбором положительной нормали n к поверхности, через которую он протекает, это правило фактически устанавливает связь между произвольно выбранным (положительным) направлением обхода контура и направлением положительной нормали к поверхности, опирающейся на этот контур. Эти направления, гласит правило, образуют правовинтовую систему (рис. 5). Во всем дальнейшем изложении мы будем его придерживаться. Итак, циркуляция B вдоль любой кривой, лежащей в перпендикулярной к току плоскости и охватывающей его, определяется формулой (7). Нетрудно видеть, что эта формула остается справедливой и для кривой, не лежащей в указанной плоскости. В самом деле, раскладывая произвольный отрезок Dl этой кривой (рис. 6) на параллельную Dl|| и перпендикулярную Dl^ току составляющие и записывая его вклад в циркуляцию, получим (B, Dl) = (B, Dl|| + Dl^) = (B, Dl||) + (B, Dl^).
Но (B, Dl|| ) = 0, ибо векторы В и Dl|| перпендикулярны, так что вклад в циркуляцию даст только составляющая Dl^, численно равная проекции вектора Dl на перпендикулярную току плоскость. Таким образом, расчет циркуляции В по произвольному контуру сводится к ее вычислению вдоль проекции этого контура на перпендикулярную плоскость (ибо индукция В от «высоты» не зависит), которое, как мы видели, дает формулу (7).
Используя принцип суперпозиции, легко обобщить доказанное утверждение на случай любого числа n прямых бесконечных токов, пронизывающих данный контур Г. Тогда
где направление обхода контура выбирается произвольно, а знаки токов – по установленному нами правилу правого винта. Соотношение (8) выражает так называемую теорему о циркуляции. Можно показать, что она справедлива в самом общем случае произвольных токов, пересекающих поверхность, опирающуюся на данный замкнутый контур Г[28] (рис. 7). Задавая направление обхода Г и получая из него ориентацию положительной нормали n, легко найти знаки входящих в (8) токов. На рис. 7, например, ток I1 вклада в циркуляцию не дает, токи I4 и I5 считаются положительными, ток I2 – отрицательным, а ток I3 пересекает поверхность дважды: один раз в направлении n, другой – навстречу ему. Поэтому и в сумму токов (8) он войдет дважды, причем с разными знаками, и, стало быть, вклада в циркуляцию тоже не даст. Понятно, что если выбрать на рис. 7 поверхность S сильно выпуклой вверх, то ток I3 вовсе ее не «зацепит».
Но, может быть, при деформации S появятся новые токи, пронизывающие ее, или исчезнет часть старых и, таким образом, изменится правая часть (8)? Нетрудно видеть, однако, что этого не произойдет и правая часть (8) от выбора S не зависит. Для доказательства рассмотрим две произвольные поверхности S1 и S2 , опирающиеся на заданный контур Г (рис. 8). Они образуют, очевидно, одну замкнутую поверхность SS , поток вектора j через которую по условию стационарности токов (18л14) равен нулю. Применительно к нашему случаю линейных токов это и означает, что алгебраическая сумма токов, втекающих в SS через поверхность S2 , т. е. пересекающих ее в направлении n2 (связанным с направлением обхода Г правилом правого винта), равна сумме токов, вытекающих из нее через поверхность S1 (в направлении n1).
Можно сформулировать теорему о циркуляции, вообще не прибегая к поверхности S. Действительно, в силу замкнутости постоянных токов их можно разбить на 2 класса (см. рис. 9, где изображены также токи, текущие из бесконечности в бесконечность): сцепленные, как звенья цепи, с данным контуром (типа I4 и I2) и не сцепленные с ним (типа I3 и I1). Очевидно, первые будут давать вклад в циркуляцию B вдоль Г, вторые – нет. Таким образом, можно сказать, что циркуляция вектора B вдоль любого замкнутого контура Г равна (умноженной на m0) алгебраической сумме токов, сцепленных с данным контуром. При этом положительными считаются токи, образующие с направлением обхода Г правовинтовую систему, а отрицательными – систему левовинтовую. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
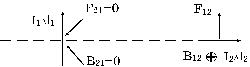 Рис. 7.
Рис. 7.
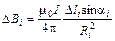 ,
,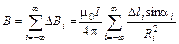 , (1)
, (1)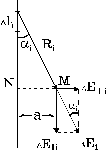 Рис. 2.
Рис. 2.
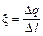 ,
,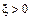 ) вдоль радиуса, проведенного из Dli в M. Однако вклад в общее поле будет давать только нормальная ее составляющая DE^i , ибо любому Dli найдется симметричный относительно точки N (отрезок MN перпендикулярен нити) участок (на рис. не показан), возбуждающий равное и противоположное DE|| i поле. Таким образом, параллельные нити составляющие для всех ее отрезков попарно взаимно уничтожатся и полное поле E будет направлено радиально (что, впрочем, очевидно и из соображений симметрии), а величина его
) вдоль радиуса, проведенного из Dli в M. Однако вклад в общее поле будет давать только нормальная ее составляющая DE^i , ибо любому Dli найдется симметричный относительно точки N (отрезок MN перпендикулярен нити) участок (на рис. не показан), возбуждающий равное и противоположное DE|| i поле. Таким образом, параллельные нити составляющие для всех ее отрезков попарно взаимно уничтожатся и полное поле E будет направлено радиально (что, впрочем, очевидно и из соображений симметрии), а величина его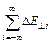 =
=  =
= 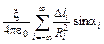 , (2)
, (2)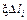 – заряд элемента нити Dli.
– заряд элемента нити Dli.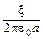 . (3)
. (3) =
= 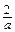 ,
, =
= 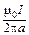 . (4)
. (4)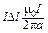 =
= 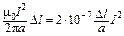 .
.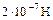 , приходящейся на каждый метр длины проводника.
, приходящейся на каждый метр длины проводника. [24] вдоль окружности радиуса a:
[24] вдоль окружности радиуса a: =
= 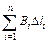 =
= 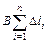 =
=  .
. Рис. 3.
Рис. 3.
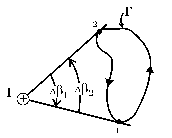 Рис. 4.
Рис. 4.
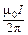 Db, (6)
Db, (6)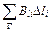 =
= 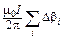 =
= 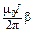 ,
,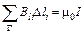 , (7)
, (7)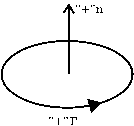 Рис. 5.
Рис. 5.
 Рис. 6.
Рис. 6.
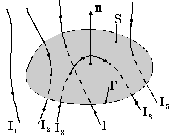 Рис. 7.
Рис. 7.
 =
=  , (8)
, (8) Рис. 8.
Рис. 8.
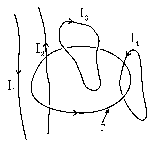 Рис. 9.
Рис. 9.