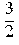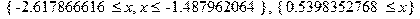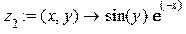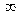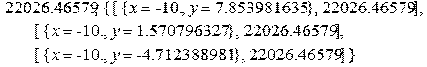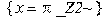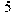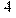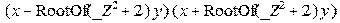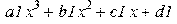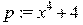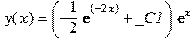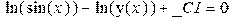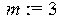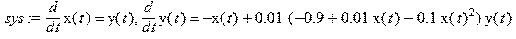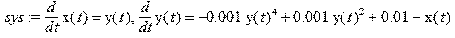Warning, the name changecoords has been redefined

Предыдущая 1 234 5 6 7 Следующая

> y := x -> abs(1 - x);

> # Накладываем условия целочисленности на переменные n и k;

> assume(n, integer); assume(k, integer);

> l := 2;

> # Расчитываем коэффициенты Фурье;

> a[0] := 1/2/l*int(y(x), x = -l..l);

> a[n] := n -> 1/l*int(y(x)*cos(n*Pi*x/l), x = -l..l);

> a[n](n);

> b[n] := n -> (1/l)*int(y(x)*sin(n*Pi*x/l), x = -l..l);

> b[n](n);

> F := (x, k) -> a[0] + sum(a[n](n)*cos(n*Pi*x/l) + b[n](n)*sin(n*Pi*x/l), n = 1..k);

> F(x, infinity);

> # Сравним насколько отличается исходная функция от ее приближения рядом Фурье;

> plot([y(x),F(x,20)],x=-2..2,color=[BLUE,RED],linestyle=[SOLID,DASHDOT],title="Функция и ее приближение",titlefont=[HELVETICA,BOLD,12],legend=["функция","приближение"],thickness=3);

Способ № 2

> # Разложение в ряд Фурье функции y(x)=sh(4x) на интервале (-Pi,Pi);

> restart; with(linalg): with(plots):

Warning, the protected names norm and trace have been redefined and unprotected

Warning, the name changecoords has been redefined

> y:=x->abs(1-x);

> `FurSer`:=proc(f,VarAndRange,n)

local l,i,t,a,b,A,B,s,Res;

if whattype(VarAndRange)<>`=` then print(`Неверно введённый диапазон`);

else s:=lhs(VarAndRange);

a:=lhs(rhs(VarAndRange));

b:=rhs(rhs(VarAndRange));

l:=(b-a)/2;

Res:=1/(2*l)*int(f(t),t=a..b);

for i from 1 to n do A[i]:=1/l*int(f(t)*cos(Pi*t*i/l),t=a..b);

B[i]:=1/l*int(f(t)*sin(Pi*t*i/l),t=a..b);

Res:=Res+A[i]*cos(Pi*i*s/l)+B[i]*sin(Pi*i*s/l);

end do;

Res;

fi;

end proc:

> z:=(x)->evalf(FurSer(y, x=-Pi..Pi,5));z(x);

> # Сравним насколько отличается исходная функция от ее приближения рядом Фурье;

> plot([y(x),z(x)],x=-Pi..Pi,color=[BLUE,RED],linestyle=[SOLID,DASHDOT],title="Функция и ее приближение",titlefont=[HELVETICA,BOLD,10],legend=["функция","приближение"],thickness=3);

1.7. Решение уравнений, неравенств и их систем

Решение линейных и нелинейных уравнений и неравенств — одна из важнейших областей математического анализа. Для решения указанного класса уравнений в аналитическом виде используется достаточно универсальная и гибкая функция solve(eqn, var) или

solve({eqn1,eqn2.....},{var1,var2....}) ,

где eqn — уравнение, содержащее функцию нескольких переменных, var — переменная, по которой ищется решение. Если при записи eqn не используется зхнак равенства или знаки отношения, считается, что solve ищет корни уравнения eqn = 0. Для получения численного решения нелинейного уравнения или системы нелинейных уравнений в форме вещественных чисел удобно использовать функцию fsolve(eqns, vars, options). Иногда бывает полезным использование и других модификаций функции solve: rsolve — для решения рекуррентных уравнений, isolve — для решения целочисленных уравнений, msolve — для решения по модулю m и других.

Решение одиночных нелинейных уравнений :

> restart;with(linalg):with(plots):

> f:=(2*x^2+3*x+1)*(3*x+1)=8*x^4;

> fsolve(f,x);

> fsolve(f,x,complex);

> solve(f,x);

> evalf(%);

> fsolve(x^5-x,x,complex);

> AA:=fsolve(2*x+(x+2)^2+(x^3-2*x)=0,x,complex);

> # Присвоение полученных значений корней, для последующего их анализа, осуществляется следующим образом:;

> AA[1];AA[2];AA[3];

Решение трансцендентных уравнений:

> restart;

> f1:=sin(x); f2:=cos(x)-1;G1:=f1-f2; s:=fsolve(G1,x);

> fsolve(sin(x)=Pi/4,x,complex);

> A:=solve(a*x^2+b*x+c,x):

> A[1];

> A[2];

> BB:=evalf(solve(a*x^3+b*x^2+c*x+d,x)):

> x[1]:=BB[1];

> x[2]:=BB[2];

> x[3]:=BB[3];

Решение систем линейных уравнений:

> restart: with(linalg): with(plots):

> sys:={3*x+5*y=15,y=x-1};

> sols:=solve(sys,{x,y});sols[1];sols[2];

> # Присвоение полученных значений решения осуществляется следующим образом:

> x2:=rhs(sols[2]);# right-hand side (правая часть выражения);

> y2:=rhs(sols[1]);

> # или с использованием оператора assign:;

> assign(sols);x;y;

> # Проверка правильности полученного решения;

> subs(sols,sys);

> x1:=subs(sols,x);

> y1:=subs(sols,y);

> implicitplot(sys,x=-10..10,y=-10..10,thickness=3,color=blue);

> restart: with(plots):

> sys:={3*x-3*y=10,2*x+y=7,y=2*x+z+4};

> sols:=solve(sys,{x,y,z});

> # Проверка правильности полученного решения;

> subs(sols,sys);

> x2:=subs(sols,x);

> y2:=subs(sols,y);

> z2:=subs(sols,z);

> implicitplot3d(sys,x=-10..10,y=-10..10,z=-15..0,style=patchcontour,orientation=[-25,30]);

Решение систем нелинейных и трансцендентных уравнений:

> restart;

> solve({x*y=a,x+y=b},{x,y});

> allvalues(%);

> restart: with(plots):

Warning, the name changecoords has been redefined

> z1:=2*x+4*y-6;

> z2:=y+(1/x)-1;

> eqs:={z1,z2};

> r:=solve(eqs,[x,y]);

> # Проверка правильности полученного решения;

> eval(eqs,r[1]);

> eval(eqs,r[2]);

> implicitplot(eqs,x=-10..10,y=-10..10,thickness=3,color=blue);

> # Решение системы нелинейных уравнений {x^2-y^2=1,x^2+xy=2};

> eqq:={x^2-y^2=1,x^2+x*y=2};

> _EnvExplicit:=true;

> ss:=solve(eqq,{x,y});

> simplify(ss[1]);

> simplify(ss[2]);

> # Решение тригонометрического уравнения {5sin(x)+12cos(x)=13};

> _EnvAllSolutions:=true:

> solve(5*sin(x)+12*cos(x)=13,x);

> evalf(%);

Решение неравенств:

> restart:

> solve(5*x>0,x);

> solve(5*x>=10,x);

> solve(a*x>b,{x});

> restart:

> eqns:=abs(z)^2/(z+1)<exp(2)/(exp(1)-1);

> AA:=solve(eqns,{z});

> evalf(AA);

> restart:

> eqns:=exp(x)*x^2>=1/2;

> SS:=solve(eqns,{x});

> evalf(SS);

> restart:

> eqns:=abs((z+abs(z+2))^2-1)^2=9;

> solve(eqns,{z});

Решение систем неравенств:

> eqns:={x^2<=1,y^2<=1,x+y<1/2};

> solve(eqns,{x,y});

> solve({x*y*z>0,x>-1,y+z>10},{x,y,z});

> {z = 0, 10 < y, -1 < x}, {10 < z, y = 0, -1 < x};

> # Отображение областей, представленных системой неравенств;

> restart:

> with(plots):

> inequal({x+y>-1,x-y<=1,y<=2+0.1*x},x=-4..4,y=-4..4,optionsfeasible=(color=magenta),optionsopen=(color=blue,thickness=2),optionsclosed=(color=black,thickness=3),optionsexcluded=(color=yellow));

> inequal({0<y,y<4,y/2+1<x,x<7-y},x=-4..10,y=0..4,optionsfeasible=(color=magenta),optionsopen=(color=blue,thickness=2),optionsclosed=(color=black,thickness=3),optionsexcluded=(color=yellow));

1.8. Анализ функций

При выполнении курсовых, дипломных и научно-исследовательских работ приходится проводить анализ поведения функций. В некоторых случаях — это сложная и трудоемкая процедура. Автоматизировать этот процесс возможно с помощью предлагаемых ниже функций.

Поиск экстремумов функций:

> restart: with(plots):with(linalg):

> # Используем функцию extrema(expr,constrs,vars,'s'), где expr - вид функции, constr - ограничения,vars- аргументы функции, s - найденная абсцисса точки экстремума;

> y:=(x)->a*x^2+b*x+c;

> extrema(y(x),{},x,'s');# при отсутствии ограничений записывается пустой список {};

> s;subs(x=s,y(x));

> extrema(x*exp(-x),{},x,'s');evalf(%);

> s;

> plot(x*exp(-x),x=0..3);

> evalf(extrema(sin(x)^2,{},x,'s'));s;

> plot(sin(x)^2,x=-Pi..Pi);

Поиск минимума или максимума функции от двух переменных:

> restart: with(plots):

> z[1]:=(x,y)->x^2-3*x+y^2+3*y+3;

> minimize(z[1](x,y));

> minimize(z[1](x,y),location);

> plot3d(z[1](x,y),x=-5..5,y=-5..5,color=blue,thickness=1,axes=boxed);

> z[2]:=(x,y)->sin(y)*exp(-x);

> maximize(z[2](x,y));

> maximize(z[2](x,y),location);

> maximize(z[2](x,y),x=-10..10,y=-10..10,location);

> evalf(%);

> plot3d(z[2](x,y),x=-10..10,y=-10..10,color=blue,thickness=1,axes=boxed);

Анализ функций на непрерывность, сингулярность:

> restart:

> iscont(1/x^2,x=-1..1);# isfunctioncontinue?;

> iscont(1/x^2,x=0..1);

> iscont(1/x^2,x=0..1,'closed');

> iscont(1/x^2,x=-1..1,'closed');

> iscont(1/(x+2),x=-1..1);

> singular(ln(x)/(x^2-x));

> singular(tan(x));evalf(%);

> singular(1/sin(x));evalf(%);

> singular(x+y+1/x,{x,y});

Операции с полиномами:

> # Выделение коэффициентов полиномa p(x);

> restart:

> p:=a[4]*x^4+a[3]*x^3+a[2]*x^2+a[1]*x+a[0];

> coeff(p,x);# выделение коэффициента при x^1;

> coeff(p,x^3); coeff(p,x,3); # выделение коэффициента при x^3;

> coeffs(p,x);# выделение всех коэффициентов по возрастанию степени;

> collect(p,x);

> # Выделение коэффициентов полиномa q(x,t);

> q:=x^2+2*(t^2)+3*x+4*t+5;

> coeffs(q);

> coeffs(q,t);

> collect(q,x);

> collect(q,x,t);

> # Оценка коэффициентов полинома по степеням;

> restart:

> q:=1/x^2+2/x+3+4*x+5*x^2;

> lcoeff(q,x);# коэффициент при старшей степени x;

> lcoeff(q,x,'t'); t;

> coeffs(q,x,'t');t;

> p:=a[4]*x^4+a[3]*x^3+a[2]*x^2+a[1]*x+a[0];

> degree(p,x);# Высшая степень полинома;

> ldegree(p,x);# Низшая степень полинома;

> # Разложение полинома по степеням;

> restart:

> evala(AFactor(2*x^2+4*x-6));

> evala(AFactor(x^2+2*y^2));

> expand((x-1)*(x-2)*(x-3)*(x-4));

> AFactor(%);

> evala(%);

> expand((x-1+I+2)*(x+1-I*2)*(x-3));

> evala(AFactor(x^2-2*y^2));

> # Вычисление корней полинома;

> restart:

> p:=x^4+9*x^3+31*x^2+59*x+60;

> solve(p,x);# все корни полинома;

> roots(p,x);# вещественные корни полинома с учетом кратности;

> expand((x-1)*(x-2)*(x-3)*(x-4));

> roots(%,x);

> # Основные операции с полиномами;

> restart:

> readlib(psqrt);# подключение библиотек;

> readlib(proot);

> psqrt(x^2+2*x*y+y^2); # корень квадратный от выражения в функции psqrt;

> proot(x^3+3*x^2+3*x+1,3); # корень кубический от выражения в функции proot;

> psqrt(x+y);

> proot(x+y,3);

> p1:=a1*x^3+b1*x^2+c1*x+d1;

> p2:=a2*x^3+b2*x^2+c2*x+d2;

> p1+p2;# сумма полиномов;

> p1*p2;# произведение полиномов;

> collect(%,x);# упорядочивание полинома по убыванию степеней x;

> p3:=p1/p2; # деление полиномов;

> expand(%,x);

> normal(%);# приведение дроби к нормальному виду;

> diff(p1,x);# производная от полинома;

> diff(p1,x$2);

> Int(p1,x)=int(p1,x);# неопределенный интеграл от полинома;

> Int(p1,x=0..1)=int(p1,x=0..1); # определенный интеграл от полинома;

> p3;

> denom(p3);# знаменатель дроби;

> numer(p3); # числитель дроби;

> collect(denom(p3),x);

> collect(numer(p3),x);

на множители полинома;

> restart:

> p:=x^4+4;

> factor(p);

> # Разложение

> factor(p,complex);

> factor(x^5-6*x^4+9*x^3-6*x^2+8*x,complex);

> ifactor(453);

> # наименьший общий делитель (н.о.д) двух полиномов;

> s[1]:=x^2-x*sqrt(3)-sqrt(2)*x+sqrt(6);

> s[2]:=x^2-2;

> gcd(s[1],s[2]);# н.о.д двух полиномов;

1.9. Решение дифференциальных уравнений и их систем

Дифференциальные уравнения лежат в основе математического моделирования различных, по своей природе, динамических систем и процессов. В настоящем разделе рассматриваются функции, реализующие аналитическое и численное решение линейных и нелинейных дифференциальных уравнений и их систем. Рассматриваются обыкновенные дифференциальные уравнения, системы уравнений и уравнения в частных производных. Для решения системы дифференциальных уравнений (задача Коши) используется функция dsolve в разных формах записи:

dsolve(ode); dsolve(ode, y(x), extra_args); dsolve({ode,ics}, y(x), extra_args); dsolve({sysode,ics}, {funcs}, extra_args),

где ode — обыкновенное дифференциальное уравнение или система уравнений, y(x) — искомая функция одной переменной, ics — выражение, задающее начальные условия, {sysode} — множество дифференциальных уравнений (система), {funcs} — множество определяемых функций, extra_args — опция, задающая тип решения. Параметр extra_args принимает может принимать следующие значения: exact — аналитическое решение (принято по умолчанию), explicit — решение в явном виде, system — решение системы дифференциальных уравнений, formal series — решение в форме степенного многочлена, series — решение в виде ряда, numeric — решение в численном виде. По умолчанию функция dsolve автоматически выбирает наиболее подходящий метод решения дифференциальных уравнений. Однако в параметрах функции dsolve в квадратных скобках можно указать предпочтительный метод решения дифференциальных уравнений. Допустимы следующие методы: quadrature, linear, Bernoulli, inverse_linear, separable, homogeneous, Chini, lin_sym, exact, Abel, pot_sym.

Решение обыкновенных дифференциальных уравнений первого порядка:

> restart:with(linalg):with(DEtools):with(plots):

> dsolve(diff(y(x),x)-a*x=0,y(x));

> dsolve(diff(y(x),x)-y(x)=exp(-x),y(x));

> dsolve(diff(y(x),x)-y(x)=sin(x)*x,y(x));

> ode_L:=sin(x)*diff(y(x),x)-cos(x)*y(x)=0;

> dsolve(ode_L,[linear],useInt);

> value(%);

> dsolve(ode_L,[separable],useInt);

> value(%);

> mu:=intfactor(ode_L);

> dsolve(mu*ode_L,[exact],useInt);

> # Графическое представление решений дифференциального уравнения, применение функции odeplot пакета plots;

> restart:with(plots):

> P:=dsolve({diff(y(x),x)=cos(x^2*y(x)),y(0)=2},y(x),type=numeric);

> odeplot(P,[x,y(x)],-15..15,labels=[x,y],color=black,thickness=2);

Решение дифференциальных уравнений второго порядка:

> restart:

> od1:=diff(y(x),x$2)-diff(y(x),x)=sin(x);

> dsolve({od1},y(x));

> dsolve({diff(y(x),x$2)-diff(y(x),x)=sin(x)},y(x));

> dsolve({diff(y(x),x$2)-diff(y(x),x)=sin(x),y(0)=0,D(y)(0)=11},y(x));# уравнение с начальными условиями;

> y(x):=rhs(%);

> y(x);

> restart:

> od2:=m*diff(y(x),x$2)-k*diff(y(x),x);

> yxo:=y(0)=0,D(y)(0)=1; # Задание начальных условий;

> dsolve({od2,yxo},y(x));

Решение систем дифференциальных уравнений (в явном виде, в виде ряда, с использованием преобразования Лапласа):

> restart:

> sys:=diff(y(x),x)=2*z(x)-y(x)-x,diff(z(x),x)=y(x);

> fncs:={y(x),z(x)};

> A:=dsolve({sys,y(0)=0,z(0)=1},fncs); # решение системы уравнений в явном виде (exact);

> A[1];

> z(x):=rhs(%);

> A[2];

> y(x):=rhs(%);

> restart:

> sys:=diff(y(x),x)=2*z(x)-y(x)-x,diff(z(x),x)=y(x);

> fncs:={y(x),z(x)};

> B:=dsolve({sys,y(0)=0,z(0)=1},fncs,series); # решение системы уравнений в виде ряда;

> y(x):=rhs(B[1]);

> z(x):=rhs(B[2]);

> restart:

> sys:=diff(y(x),x)=2*z(x)-y(x)-x,diff(z(x),x)=y(x);

> fncs:={y(x),z(x)};

> Order:=8;# задаем порядок приближения рядом (по умолчанию 6);

> B:=dsolve({sys,y(0)=0,z(0)=1},fncs,series);

> y(x):=rhs(B[1]);

> z(x):=rhs(B[2]);

> restart:

> sys:=diff(y(x),x)=2*z(x)-y(x)-x,diff(z(x),x)=y(x);

> fncs:={y(x),z(x)};

> dsolve({sys,y(0)=0,z(0)=1},fncs,method=laplace);# решение системы уравнений с использованием преобразования Лапласа;

Численное решение системы дифференциальных уравнений:

> restart:

> sys:=diff(y(x),x)=2*z(x)-y(x)-x,diff(z(x),x)=y(x);

> fncs:={y(x),z(x)};

> F:=dsolve({sys,y(0)=0,z(0)=1},fncs,numeric); # решение уравнения по методу Рунге-Кутта-Фелберга;

> F(2);

Ø plots[odeplot](F,[x,y(x)],0..2.5,labels=[x,y],color=red); # построения графика y(x) решения;

> plots[odeplot](F,[x,z(x)],0..2.5,labels=[x,z],color=red); # построения графика z(x) решения;

> restart:with(plots):

> sys:=diff(y(x),x)=z(x),diff(z(x),x)=3*sin(y(x));

> fncs:={y(x),z(x)};

> P:=dsolve({sys,y(0)=0,z(0)=1},fncs,type=numeric);

> odeplot(P,[[x,y(x)],[x,z(x)]],-4..4,numpoints=25,color=red,thickness=2);# построение графиков y(x) и z(x) в одних осях;

Решение системы двух дифференциальных уравнений с выводом фазового портрета решения:

> restart:with(plots):

> sys:=diff(y(x),x)=z(x),diff(z(x),x)=3*sin(y(x));

> fncs:={y(x),z(x)};

> P:=dsolve({sys,y(0)=0,z(0)=1},fncs,type=numeric);

Ø odeplot(P,[y(x),z(x)],-4..4,numpoints=150,color=red,thickness=2);

Решение дифференциальных уравнений с кусочно-линейными функциями:

> restart:

> eq:=diff(y(x),x)+piecewise(x<x^2-3,exp(x/2))*y(x);

> dsolve(eq,y(x));

Гармонический осциллятор:

> restart:

> F:=(t)->A*sin(nu*t);

> ode:=diff(q(t),t$2)+2*delta*diff(q(t),t)+omega[0]^2*q(t)=F(t)/m;

> m:=3; delta:=0.1; omega[0]:=150; A:=20; nu:=2;# Задание параметров системы;

> yx0:=q(0)=1,D(q)(0)=0; # Задание начальных условий;

> dsolve({ode,yx0},q(t)); # Решение дифференциального уравнения (точное - exact);

> q(t):=rhs(%);

> plot(q(t),t=0..15); # Построение графика решения;

Решение уравнения Риккати:

> restart:

> eq:=diff(y(x),x)=piecewise(x>0,x)*y(x)^2;

> dsolve({y(0)=1,eq},y(x));

> # Проверка решения;

> simplify(eval(subs(%,eq)));

Решение дифференциальных уравнений в частных производных:

> restart:

> Diff(u(x,t),t,t)=a^2*Diff(u(x,t),x,x);

> # начальные условия; u(x,0)=f(x),Diff(u(x,t),t)=0 при t=0, - infinity < x < infinity,t>=0;

> eqn:=diff(u(x,t),t$2)-a^2*diff(u(x,t),x$2)=0;

> pdsolve(eqn);

> # _F1(at+x) и _F2(at-x) - произвольные дважды дифференцируемые функции;

> u:=unapply(rhs(%),x,t); # задаем u как функцию двух параметров x и t;

> # воспользуемся тем, что производная по времени от u(x,t) при t=0 равна нулю;

> D[2](u)(x,0)=0;

> dsolve(%,_F1(x));

> _F1:=F;

> _F2:=x->F(-x);

> u(x,t);

> u(x,0);

> f:=x->1/5*(1-abs(x))*Heaviside(1-abs(x));

> F:=(1/2)*f;

> a:=1;

> evalf(u(x,t));

Осциллятор Ван-дер-Поля

Классическая модель нелинейной системы, демонстрирующая периодические автоколебания.

При различных начальных условиях фазовая траектория стремится к аттрактору — предельному циклу.

Установившиеся движения представляют собой периодические колебания, математическим образом в фазовом пространстве которых и является предельный цикл.

> restart;with(DEtools):with(plots):

> vdp:=diff(x(t),t,t)-2*delta*diff(x(t),t)*(1-alpha*x(t)^2)+omega^2*x(t)=0;

> alpha:=1;omega:=1;d:=0.2;

> sys:=[diff(x(t),t)=y(t),diff(y(t),t)-2*delta*y(t)*(1-alpha*x(t)^2)+omega^2*x(t)=0];

> ff:=dsolve({sys[1],subs(delta=d,sys[2]),x(0)=1,y(0)=1},

{x(t),y(t)}, type=numeric, output=listprocedure);

> fp := subs(ff,x(t)): fw := subs(ff,y(t)):

> steps:=100; init_t:=0; fin_t:=15*Pi;

> g:=seq([fp((fin_t-init_t)/steps*i),fw((fin_t-init_t)/steps*i)],i=0..steps):

> h:=seq([(fin_t-init_t)/steps*i,fp((fin_t-init_t)/steps*i)],i=0..steps):

Фазовый портрет;

Ø pointplot([g],connect=true,color=red,title="phase portrait",labels=[coordinate,velocity]):

Решение;

> pointplot([h],connect=true,color=red,title="oscillations",labels=[t,coordinate]):

> ic:=[[x(0)=3,y(0)=2],[x(0)=2,y(0)=0],[x(0)=0.5,y(0)=0.5],[x(0)=0,y(0)=0]];

> DEplot(subs(delta=d,sys),[x(t),y(t)],t=0..15*Pi,ic,method=rkf45,linecolor=black,color=blue,stepsize=0.1,title="Van-der-Pole Oscillator"):

> # При изменении параметра delta происходит изменение формы аттрактора, при этом его топология не меняется;

> for i from 1 by 1 to 15 do

> #delta:=i/20;

> fp[i]:=DEplot(subs(delta=i/20,sys),[x(t),y(t)],t=0..15*Pi,ic,method=rkf45,linecolor=black,color=blue,stepsize=0.1,title="Van-der-Pole Oscillator"):

> end do:

> display(seq(fp[i],i=1..15),insequence=true);

> restart;with(DEtools):

> mu:=0.01:alpha:=0.1:beta:=0.1:sys:=diff(x(t),t)=y(t),diff(y(t),t)=-x(t)+mu*(-1+alpha*(1+beta*x(t)-x(t)^2))*y(t);

> DEplot3d({sys},[x(t),y(t)],t=0..80, [[x(0)=10,y(0)=10]],stepsize=0.1,orientation=[0,90],method=classical[abmoulton],corrections=3,axes=NORMAL,linecolor=blue);

> restart;with(DEtools):

> mu:=0.01:sys:=diff(x(t),t)=y(t),diff(y(t),t)=-x(t)+mu*(1-x(t)^2)*y(t);

> f1:= (1-R^2*cos(u)*cos(u))*(-R*sin(u))*sin(u);

> FR:=-1./(2.*Pi)*Int(f1,u=0..2*Pi)=-1./(2.*Pi)*int(f1,u=0..2*Pi);

> f2:= (1-R^2*cos(u)*cos(u))*(-R*sin(u))*cos(u);

> _FR:=1./(2.*Pi)*Int(f2,u=0..2*Pi)=1./(2.*Pi)*int(f2,u=0..2*Pi);

> with(DEtools):

> DEplot3d({sys},[x(t),y(t)],t=0..25, [[x(0)=2,y(0)=2],[x(0)=0.5,y(0)=0.5],[x(0)=5,y(0)=5]],stepsize=0.1,orientation=[0,90],method=classical[abmoulton],corrections=3,axes=NORMAL,linecolor=blue);

> restart;with(DEtools):

> mu:=0.01:alpha:=0.1:beta:=0.1:sys:=diff(x(t),t)=y(t),diff(y(t),t)=-mu*(alpha*y(t)^4-beta*y(t)^2-1)-x(t);

> DEplot3d({sys},[x(t),y(t)],t=0..10, [[x(0)=1,y(0)=1]],stepsize=0.1,orientation=[0,90],method=classical[abmoulton],corrections=3,axes=NORMAL,linecolor=blue);

> restart;with(DEtools):

> fun:=mu*(1+b*y(t)^2-a*y(t)^4);

Предыдущая 1 234 5 6 7 Следующая

Не нашли, что искали? Воспользуйтесь поиском по сайту: