
|
|
Графический метод решения задачи линейного программирования.Общая формулировка задач линейного программирования.
Найти вектор X=(x1,x2,…,xn), который удовлетворяет системе линейных ограничений и обеспечивает экстремальное (минимальное или максимальное) значение целевой функции. Ограничения могут быть сформулированы в виде равенств или неравенств. В зависимости от этого различают различные формы записи задач линейного программирования.
Дано: система линейных ограничений, в которой S равенств и (m-S) неравенств
(2) (3) Требуется найти такое решение системы (1) X=(x1,x2,…,xn), которое удовлетворяет условию (2), и на котором целевая функция достигает экстремума (максимума или минимума).
В ней ограничение (1) содержит только неравенства (3) (1) (2)
(3) (1) (2)
Ограничение (1) содержит только равенства (3) (1) (2) Определение. Вектор X=(x1,x2,…,xn), координаты которого являются решением ограничений (1) и (2), называется допустимым решением ЗЛП. Множество всех допустимых решений задачи называется областью допустимых решений (ОДР). Допустимое решение X, на котором целевая функция достигает максимума или минимума, называется оптимальным решением задачи.
Переход от одной формы записи ЗЛП к другой. Теорема. Пусть дано линейное неравенство с n переменными и переменная такая, что тогда Доказательство: (достаточность)→: Пусть X=(α1, α 2,…, α n) – решение (4), т.е. Введём αn+1 =bi- при этом Пусть выполняется (5’) и (6’). Отбросив в левой части уравнения (6’) Теорема позволяет от неравенств в системе ограничений перейти к уравнениям и, наоборот, от уравнения перейти к неравенству.
Графический метод решения задачи линейного программирования. Этот метод имеет ограниченную область применения. Этим методом можно решать следующие задачи:
Задача типа 2 сводится к задаче типа 1, для чего нужно перейти от канонической к симметричной форме записи. Рассмотрим решение задач типа 1. Найти X=(x1,x2), который является решением (1), удовл. (2),
(2) x1≥0, x2≥0 и на котором целевая функция f(X)=c1x1+c2x2 (3) достигает экстремума (максимума или минимума). Решение задачи содержит два этапа: I. Построим ОДР
ОДР находится в 1-й координатной четверти система (1) содержит линейные неравенства с двумя переменными (7) Решением такого неравенства является любая пара чисел (x1;x2), которая при подстановке в (7) обращает его в верное числовое равенство. На координатной плоскости (x1;x2) – точка . Множество решений (7) – некоторое множество точек на x1Ox2. Выясним, какую область на плоскости x1Ox2 образуют точки, которые являются решением ограничений (1) и (2). Заменим неравенство (7) соответствующим ему равенством.
это уравнение определяет на плоскости x1Ox2 прямую линию. Эта линия делит плоскость x1Ox2 на 2 полуплоскости π1 и π2. Утверждение. Точки одной из этих полуплоскостей являются решением
а точки другой полуплоскости являются решением неравенства Докажем это утверждение. Доказательство: Возьмём т. M1 (x1’, x2’), М1 М0 – проекция т. М1
М0 Выясним знак выражения т.
Знак выражения зависит от знака 1)
2) Тогда
Для того, чтобы определить полуплоскость, в которой выполняются соответствующие неравенства, достаточно подставить в неравенство координаты какой-либо одной точки, не лежащей на граничной прямой. Если неравенство удовлетворяется, то областью решения будет полуплоскость, в которой находится эта точка; если нет – то в другой. Чтобы построить ОДР на координатной плоскости x10x2, нужно построить граничные прямые и области решений каждого неравенства системы; пересечение областей решения этих неравенств, взятое в первом квадранте и будет областью решений данной задачи. II. Нахождение ОДР оптимального решения задачи. Рассмотрим уравнение
Определение. Линия уровня, имеющая общие точки с ОДР и расположенная так, что ОДР целиком находится в одной из полуплоскостей, на которые данная линия уровня делит координатную плоскость, называется опорной прямой. Чтобы найти ОДР оптимального решения, выполним: 1. Строим 2. Перпендикулярно 3. Перемещая эту линию уровня в направлении 4. Совместно решив уравнения прямых, ограничивающих ОДР и имеющих общие точки с опорной прямой, найдем оптимальное решение. В зависимости от вида ОДР и целевой функции задача может иметь единственное решение, бесконечное множество решений, или не иметь решений ввиду несовместности системы ограничений или неограниченности целевой функции ОДР. Пример.
Решим совместно уравнения прямых BC и DC, и имеющих общую точку с опорной прямой, найдём оптимальное решение.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|




 i=1,2,…,m
i=1,2,…,m


 i=1,2,…,m
i=1,2,…,m i=1,2,…,m
i=1,2,…,m (4)
(4) (5)
(5) , (6)
, (6)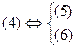 .
. (4’)
(4’) , (5’)
, (5’) . (6’)
. (6’) , получим неравенство (4’).
, получим неравенство (4’).



 - (8)
- (8) , (*)
, (*)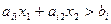 . (**)
. (**)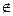 m
m ={x1’- x10; x2’- x20}
={x1’- x10; x2’- x20}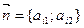
 m;
m; 
 в зависимости от того, в какой из полуплоскостей (π1,π2) находится данная точка.
в зависимости от того, в какой из полуплоскостей (π1,π2) находится данная точка.
 (*)
(*)






 (3) При конкретном значении f это уравнение определяет на плоскости прямую линию. При изменении f мы получим семейство параллельных прямых (прямые ||, т.к. они все имеют один угловой коэффициент
(3) При конкретном значении f это уравнение определяет на плоскости прямую линию. При изменении f мы получим семейство параллельных прямых (прямые ||, т.к. они все имеют один угловой коэффициент  ). Каждую из этих прямых называют линией уравнения, т.к. согласно равенству (3) на каждой такой прямой функция f сохраняет постоянное значение.
). Каждую из этих прямых называют линией уравнения, т.к. согласно равенству (3) на каждой такой прямой функция f сохраняет постоянное значение.
 - это вектор, перпендикулярный линиям уровня, и он показывает направление, по которому нужно перемещать линию уровня, чтобы значение f возрастало. Обозначим
- это вектор, перпендикулярный линиям уровня, и он показывает направление, по которому нужно перемещать линию уровня, чтобы значение f возрастало. Обозначим 
 в начале координат.
в начале координат. проводим одну из линий уровня, имеющую общие точки с ОДР.
проводим одну из линий уровня, имеющую общие точки с ОДР.