
|
|
Вершины выпуклого многогранникаНа примере задачи линейного программирования с n=2 мы видели, что особую роль играют вершины допустимой области. Но что понимать под вершиной выпуклого многогранника при n>3, когда не существует геометрически наглядного образа ? Легко заметить, что при n=2 и n=3 вершина выпуклого многогранника - это такая точка, которая не является внутренней точкой никакого отрезка, концы которого принадлежат этому многограннику (см. рис 14). Этим свойством обладают только вершины .
Определение. Вершиной или крайней точкой выпуклого многогранника называется любая его точка, которая не является внутренней точкой никакого отрезка, целиком принадлежащего этому многограннику. Докажем теперь несколько важных теорем, касающихся вершин выпуклых многогранников. Теорема 1. Любая точка выпуклого многогранника является выпуклой комбинацией его вершин. Доказательство Строгое доказательство этой теоремы - достаточно сложная задача. Поэтому мы приведем лишь идею доказательства. Пусть n=2 и мы имеем выпуклый многогранник G (см. рис. 15) с вершинами
Рис. 15
Аналогично обстоит дело и в случае n =3. Посмотрите на рисунок и попробуйте сами повторить те же рассуждения, что и выше. Выпуклой комбинацией, каких вершин является точка A , изображенная на правой части рисунка 15? В общем случае выпуклого n-мерного многогранника рассуждения выглядят примерно так. Берем любую внутреннюю точку A этого многогранника и соединяем её отрезком прямой с какой-то из вершин. Продолжим эту прямую до пересечения с какой-то из граней выпуклого многогранника. Пусть точка этого пересечения будет B .Тогда точка A будет выпуклой комбинацией этой вершины и точки B . Но что такое грань выпуклого многогранника? Это тоже выпуклый многогранник, но только размерности (n - 1). Поэтому весь процесс можно повторить для точки B , перейдя к многограннику размерности (n-2), затем (n -3) и т.д. В конце концов мы попадем на многогранник размерности 2, то есть на обычный отрезок, и точка A окажется выпуклой комбинацией некоторых вершин исходного многогранника. Теорема 2. (Основная теорема линейного программирования) Целевая функция задачи линейного программирования достигает своего экстремума (минимума или максимума) в вершине допустимой области. Если целевая функция достигает экстремального значения более, чем на одной вершине, то она достигает того же значения в любой точке, являющейся выпуклой комбинацией этих вершин. Доказательство Обозначим вершины выпуклого многогранника через Пусть для определенности мы ищем минимум Если Пусть теперь
Обозначим через m минимум из всех значений
С другой стороны, по определению оптимального плана, должно быть Для доказательства второй части теоремы допустим, что
что и доказывает теорему. Эта теорема имеет важнейшее значение, так как она указывает путь решения задачи линейного программирования. Совсем не надо перебирать всеточки допустимой области. Достаточно перебрать вершиныдопустимой области, а ведь их - конечное число. Кроме того, как это окажется далее, не нужноперебирать все вершины, можно этот перебор существенно сократить. Только вот как узнать, имеем ли мы дело с вершиной или нет? Все дальнейшее изложение будет вестись для задач линейного программирования в канонической форме в векторных обозначениях (см. п.2 главы 1). Теорема 3. Если известно, что система векторов Замечание. Заметим, что в Доказательство Предположим, что
Вычитая, их друг из друга, получим
Но в силу линейной независимости векторов
то есть Теорема 4. Если Доказательство
Докажем теорему методом от противного. Пусть система векторов
Зададимся некоторым
Выбирая a достаточно малым можно всегда добиться того, что
Но тогда Пусть число ограничений в задаче линейного программирования равно m .Так как каждая система из
Определение. План, соответствующий вершине допустимой области, называется опорным планом. Если опорный план имеет ровноm отличных от нулякомпонент,то он называется невырожденнымопорным планом. Если число ненулевых компонент опорного плана меньшеm, то он называется вырожденнымопорным планом. Проблема вырожденных опорных планов - сложная проблема. К счастью, в обычных ситуациях вырожденные опорные планы встречаются очень редко. Поэтому в этой главе мы всюду далее будем считать, что все опорные планы невырождены. 2.3. Переход от вершины к вершине Раз экстремум целевой функции достигается на одной из вершин многогранника допустимой области, то нет необходимости исследовать все точки области. Надо лишь "пройтись" по вершинам многогранника. Но для этого нужно уметь переходить от одной вершины к другой. Пусть нам известен какой-то опорный план (вершина), соответствующий m векторам из первоначальной системы n векторов. Будем считать, что
Так как векторы
где Возьмем какой-то вектор, не входящий в наш базис, скажем, вектор
Пусть хотя бы один из коэффициентов
Вектор
в случае неотрицательности всех своих компонент является планом. Те компоненты, где
Отсюда имеем:
Возьмем
где минимум берется по всем тем индексам i , для которых
где
который опять содержит ровно m отличных от нуля положительных компонент. Докажем, что это - новая вершина, то есть это -новыйопорный план. Действительно, этому новому плану соответствуют векторы
Так как разложение по базису определяется однозначно, то должно быть Отметим следующее. Если все
Переход к новому базису В старом базисе
Теперь мы перешли в новую вершину, которой соответствует базис
Выведем формулы для
выразим из него вектор
и подставим это выражение в (8). Тогда мы получим
Перегруппировывая слагаемые, получим:
что и дает разложение векторов по новому базису 2.5. Отыскание оптимального плана Пусть мы стремимся к минимуму целевой функции, то есть нашей задачей является
Очевидно, что довольно трудоемко перебирать все вершины многогранника, соответствующего допустимой области. Лучше идти по вершинам так, чтобы при переходе от вершины к вершине значение целевой функции уменьшалось. Именно в этом и состоит идея метода решения задачи линейного программирования, которая получила название симплекс - метода. Итак, основная идея симплекс-метода заключается в том, чтобы так переходить от вершины к вершине, чтобы при каждом переходе значение целевой функции уменьшалось или увеличивалось. Именно так из любой вершины можно добраться до оптимальной вершины и получить оптимальный план. Пусть известен опорный план
где все
Введем величины
где Теорема 1.9. Если для некоторого j выполняется условие
Доказательство: Попробуем ввести в базис именно вектор Умножив разложение (1.36) для
В последнем равенстве к обеим частям равенства прибавлена величина Теперь рассмотрим два случая. Случай 1. Пусть среди чисел
где минимум ищется по всем тем индексам j , для которых
так как Случай 2. Пусть все
будет стремиться к Теорема 1.10. Если для некоторого опорного плана для всех j справедливы неравенства Доказательство: Пусть
Покажем, что По предположению, все
Подставим в (1.39) вместо
и изменим порядок суммирования
Аналогично, подставляя в (1.41) для каждого j выражение
Так как система векторов
получим
то есть любой другой план имеет не меньшее значение целевой функции, чем наш опорный план. Эта теорема дает критерий оптимальности опорного плана. Теоремы 1.9 и 1.10 дают возможность, начав с некоторого исходного опорного плана, получать последовательность все более лучших опорных планов, которые завершатся либо оптимальным планом, либо будет показано, что целевая функция неограничена. Отметим следующее:
Алгоритм симплекс-метода Теперь мы в состоянии сформулировать алгоритм симплекс-метода для решения задач линейного программирования, заданных в канонической форме. Обычно он реализуется в виде так называемой симплекс-таблицы, изображенной на следующей странице. В первом столбце этой таблицы располагаются обозначения векторов, входящих в базис. Второй столбец - коэффициенты Третий столбец - компоненты опорного плана. В дополнительной строке в этом столбце пишется величина Далее идут столбцы, соответствующие всем векторам В дополнительной строке сверху обычно выписывают коэффициенты В дополнительной строке снизу пишутся величины
Заметим, что для векторов, входящих в базис, эти разности всегда равны нулю. Далее идут следующие этапы, связанные с преобразованием этой таблицы. При ручном счете каждый раз эту таблицу лучше переписывать заново, при счете на ЭВМ (который, естественно, всегда используется при решении практических, а не учебных задач), эта таблица просто преобразуется в памяти ЭВМ. Этап 1 Просматривается дополнительная строка снизу, где записаны разности .
Этап 2 Если есть столбцы, где Пусть Этап 3 Просматривается столбец, соответствующий этому вектору. Если все
Пусть этот минимум достигается для вектора
Этап 4 После того, как определены направляющие столбец и строка, начинает заполняться новая симплекс-таблица, в которой на месте направляющей
Обычно заполнение этой новой таблицы начинается именно с направляющей строки. В качестве компоненты опорного плана туда
Остальные элементы этой строки заполняются величинами
Обратите внимание на особую роль элемента Написанные выше формулы для пересчета элементов направляющей строки можно записать следующим правилом:
Этап 5 Далее начинается пересчет всех остальных строк таблицы, включая и дополнительную нижнюю строку по формулам: для компонент плана
для координат разложения по базису
для дополнительной строки
Обратите внимание на то, что все эти формулы по сути дела строятся по одному правилу
Это правило применимо и к компонентам плана, и к величинам
Далее итерации продолжаются.
Пример Решить задачу линейного программирования
В данном случае вектор
Заполним исходную симплекс-таблицу, взяв в качестве исходного базиса
Исходная симплекс-таблица
Обратите внимание на то, что из-за специфического вида векторов Ну, а величины
Первая итерация Просматривая дополнительную строку мы видим, что в ней всего один положительный элемент - в столбце, соответствующем вектору В этом направляющем столбце есть два положительных числа - 4 и 3. Поэтому нужно рассмотреть два частных
и выбрать из них наименьшее. Так как
и он достигается на векторе 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|

 .Возьмём любую его точку A и соединим отрезком с какой-то вершиной, скажем
.Возьмём любую его точку A и соединим отрезком с какой-то вершиной, скажем  . Продолжим эту прямую до пересечения с какой-то стороной многогранника и обозначим точку этого пересечения через B
. Продолжим эту прямую до пересечения с какой-то стороной многогранника и обозначим точку этого пересечения через B

 и
и 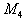 .
.

 .
. . Пусть оптимальный план есть
. Пусть оптимальный план есть  . Это означает, что
. Это означает, что 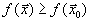 для всех
для всех 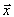 из допустимой области.
из допустимой области.


 , и пусть он достигается
, и пусть он достигается

 ,
,

 . Сравнивая, получим, что
. Сравнивая, получим, что  , то есть существует такая вершина
, то есть существует такая вершина  , где целевая функция достигает того же минимального значения.
, где целевая функция достигает того же минимального значения. . Тогда
. Тогда  Если
Если 
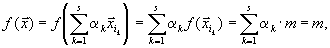
 линейно независима и такова, что
линейно независима и такова, что  где все
где все 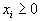 , то точка
, то точка  является вершиной допустимой области.
является вершиной допустимой области. и
и ,что
,что 


 ,
, .
. .
.
 . Следовательно,
. Следовательно,  вершина, то вектора
вершина, то вектора  , соответствующие отличным от нуля компонентам
, соответствующие отличным от нуля компонентам  , образуют линейно независимую систему.
, образуют линейно независимую систему. .
.
 , не все равные нулю, что
, не все равные нулю, что .
.
 и умножим на него обе части предыдущего равенства (2). Прибавляя и вычитая полученный результат из (1), получим
и умножим на него обе части предыдущего равенства (2). Прибавляя и вычитая полученный результат из (1), получим
 будут больше нуля для всех
будут больше нуля для всех  (для этого достаточно взять
(для этого достаточно взять  , где минимум берется по всем тем i , для которых
, где минимум берется по всем тем i , для которых  . Тогда мы получим два плана
. Тогда мы получим два плана ,
, .
. , что противоречит тому, что
, что противоречит тому, что  векторов в m-мерном пространстве линейно зависима, то среди компонент плана, соответствующего вершине, не более m отличных от нуля компонент.
векторов в m-мерном пространстве линейно зависима, то среди компонент плана, соответствующего вершине, не более m отличных от нуля компонент.
 .
.
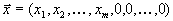 ,
, .
.
 .
.
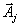
 ,
,
 - коэффициенты разложения по базису (координаты вектора
- коэффициенты разложения по базису (координаты вектора  . Для него
. Для него .
.
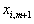 положителен. Возьмем некоторую величину
положителен. Возьмем некоторую величину  , умножим на неё обе части равенства (5) и вычтем из (3). Тогда получим
, умножим на неё обе части равенства (5) и вычтем из (3). Тогда получим

 , будут автоматически неотрицательны. Чтобы остальные компоненты были неотрицательны, надо, чтобы
, будут автоматически неотрицательны. Чтобы остальные компоненты были неотрицательны, надо, чтобы

 ,
, . Очевидно, что если
. Очевидно, что если  , то все компоненты плана
, то все компоненты плана  будут неотрицательны.
будут неотрицательны. .
.

 .
.

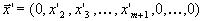 ,
,
 . Допустим, что они линейно зависимы, то есть существуют такие числа
. Допустим, что они линейно зависимы, то есть существуют такие числа  , не все равные нулю, что векторы
, не все равные нулю, что векторы
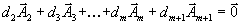 уже были линейно независимы, поэтому
уже были линейно независимы, поэтому  . Но тогда
. Но тогда  ,где
,где  . Но раньше у нас было (см. (5))
. Но раньше у нас было (см. (5)) .
. , в частности, должно быть
, в частности, должно быть  =0. Это противоречит тому, что
=0. Это противоречит тому, что  , то мы не в состоянии проделать эту процедуру. Зато, неограниченно увеличивая , мы можем получить план со сколь угодно большими компонентами. Значит, в этом случае допустимая областьнеограничена
, то мы не в состоянии проделать эту процедуру. Зато, неограниченно увеличивая , мы можем получить план со сколь угодно большими компонентами. Значит, в этом случае допустимая областьнеограничена .
.
 . Мы должны вывести из базиса вектор
. Мы должны вывести из базиса вектор 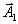 и ввести туда вектор
и ввести туда вектор 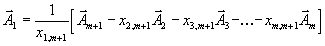




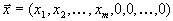 и связанная с ним система линейно независимых векторов
и связанная с ним система линейно независимых векторов 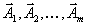 . Тогда имеем
. Тогда имеем

 - коэффициенты целевой функции и
- коэффициенты целевой функции и  - её значение, соответствующее данному опорному плану. Поскольку векторы
- её значение, соответствующее данному опорному плану. Поскольку векторы  можно разложить по этим векторам:
можно разложить по этим векторам:

 ).
).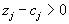 , то можно уменьшить значение целевой функции, причем:
, то можно уменьшить значение целевой функции, причем: на q и вычтя их из (1.34) и(1.35), получим
на q и вычтя их из (1.34) и(1.35), получим ,
,

 .
. есть хотя бы одно положительное число. Возьмем
есть хотя бы одно положительное число. Возьмем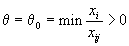 ,
, . Тогда, как это было показано выше, получится новый опорный план. Для него значение целевой функции будет равно
. Тогда, как это было показано выше, получится новый опорный план. Для него значение целевой функции будет равно ,
, и
и  . Тогда q можно брать сколь угодно большим и при этом новый план всегда будет планом, так как будет удовлетворять всем ограничениям. Но, при неограниченном увеличении q , значение целевой функции, равное
. Тогда q можно брать сколь угодно большим и при этом новый план всегда будет планом, так как будет удовлетворять всем ограничениям. Но, при неограниченном увеличении q , значение целевой функции, равное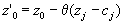
 , то есть значение целевой функции может быть сделано сколь угодно малым. Теорема доказана.
, то есть значение целевой функции может быть сделано сколь угодно малым. Теорема доказана. , то он является оптимальным.
, то он является оптимальным. - произвольный план. Тогда имеем
- произвольный план. Тогда имеем
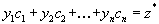
 .
. . Кроме того, все
. Кроме того, все  . Поэтому
. Поэтому
 их разложения по базису
их разложения по базису
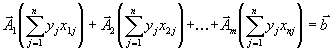

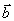 по базису
по базису 
 ,
, минимум достигается при нескольких i, то для вывода из базиса обычно берут вектор
минимум достигается при нескольких i, то для вывода из базиса обычно берут вектор  , вводимого в базис, обычно берут тот вектор
, вводимого в базис, обычно берут тот вектор  наибольшая
наибольшая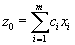 . Её легко вычислить перемножая числа из второго столбца и третьего столбца и складывая их.
. Её легко вычислить перемножая числа из второго столбца и третьего столбца и складывая их. , вычисляемые по формулам:
, вычисляемые по формулам: .
. ,
,
 , то выбирается столбец с максимальным значением этой разности. Индекс j определит вектор, вводимый в базис.
, то выбирается столбец с максимальным значением этой разности. Индекс j определит вектор, вводимый в базис. , то есть в базис надо вводить вектор
, то есть в базис надо вводить вектор  . Назовем столбец, соответствующий этому вектору, направляющим столбцом. В дальнейшем мы будем направляющий столбец помечать символом
. Назовем столбец, соответствующий этому вектору, направляющим столбцом. В дальнейшем мы будем направляющий столбец помечать символом 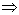 .
.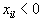 , то значения целевой функции неограничены снизу. Если есть
, то значения целевой функции неограничены снизу. Если есть  , то находятся
, то находятся
 ,
,
 . Тогда именно вектор
. Тогда именно вектор 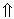 .
.
 .
. .
. , стоящего на пересечении направляющей строки и направляющего столбца. Именно на него делятся все бывшие элементы направляющей строки. На месте бывшего элемента
, стоящего на пересечении направляющей строки и направляющего столбца. Именно на него делятся все бывшие элементы направляющей строки. На месте бывшего элемента 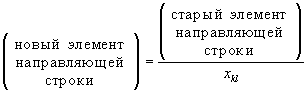 .
. ;
; ;
; .
.
 .
.


 равен (0,1,-3,0,2,0), а в векторной форме ограничения могут быть записаны в виде
равен (0,1,-3,0,2,0), а в векторной форме ограничения могут быть записаны в виде .
. ,
,



 в столбец "план" просто переписался вектор
в столбец "план" просто переписался вектор  приходится считать:
приходится считать:


