
|
|
Примеры моделей, приводящих к задачам линейного программированияЛинейное программирование
Часть I
Содержание:
1. Основные понятия. 3 1.1.Примеры моделей, приводящих к задачам линейного программирования. 3 1.2. Стандартная и каноническая формы задачи линейного программирования. 8 1.3. Геометрическая интерпретация задач линейного программирования. 16 2. Симплекс-метод. 24 2.1. Выпуклые множества и многогранники. 24 2.2. Вершины выпуклого многогранника. 29 2.3. Переход от вершины к вершине. 35 2.4. Переход к новому базису. 38 2.5. Отыскание оптимального плана. 40 2.6. Алгоритм симплекс-метода. 44 2.7. Метод искусственного базиса. 50 3. Двойственные задачи. 55 3.1. Постановка двойственных задач. 55 3.2. Свойства двойственных задач. 58 3.3. Двойственный симплекс-метод. 64 4. Транспортная задача. 65 4.1. Постановка задачи. 65 4.2. Простейшие свойства транспортной задачи. 67 4.3. Методы определения первоначального опорного плана. 69 4.3.1. Построение исходного опорного плана (метод северо-западного угла) 69 4.3.2. Метод минимального (максимального) элемента. 73 4.3.3. Метод аппроксимации Фогеля. 75 4.3.4. Метод двойного предпочтения. 76 4.4. Методы проверки опорного плана на оптимальность. 78 4.4.1. Потенциалы. Критерий оптимальности плана. 78 4.4.2. Дельта-метод. 83 4.5. Алгоритм улучшения плана. 85 4.6. Снятие вырожденности. 91 4.6.1. Эпсилон-прием.. 91 4.6.2. 0-подстановка. 95
Примеры моделей, приводящих к задачам линейного программирования Линейное программирование является одной из основных частей того раздела современной математики, который получил название математического программирования. В общей постановке задачи этого раздела выглядят следующим образом. Имеются какие-то переменные
В зависимости от вида функции Линейное программирование характеризуется тем, что
б) область G определяется системой линейных равенств или неравенств. Чтобы понять, откуда берутся задачи линейного программирования, рассмотрим некоторые, уже ставшие классическими, примеры подобных задач. Задача о диете Задача о диете возникает при составлении наиболее экономного (т.е. наиболее дешевого) рациона питания животных, удовлетворяющего определенным медицинским требованиям. Предположим, что в нашем распоряжении имеется n продуктов питания (сено, зерно, комбикорм, соль и т.д.). Обозначим эти продукты через
Рациональная диета должна доставлять животному определенные компоненты (белки, жиры, углеводы, витамины, микроэлементы и т.д.). Обозначим эти компоненты через
Таким образом, величина Рацион кормления должен указать, какое количество
Что же требуется от рациона? Во-первых, должны быть выполнены определенные медицинские требования, которые заключаются в том, что за указанный срок животное должно получить не менее определенного количества каждого компонента (не менее определенного количества белков, жиров, витаминов и т.д.). Обозначим через
Пусть у нас имеется
Естественно, мы стремимся получить за нашу продукцию возможно больше. Поэтому стоящая перед нами задача составления плана производства приобретает вид:
У нас снова получилась линейная целевая функция,и ограничения снова имеют характер линейных неравенств. Таким образом, мы снова имеем дело с задачей линейного программирования. Мы не будем рассматривать примеры других задач линейного программирования. Отметим лишь, что они встречаются очень часто при оптимизации самых разнообразных производственных и экономических задач 1.2. Стандартная и каноническая формы задачи линейного программирования Обратите внимание на то, что в указанных выше двух примерах задачи имели достаточно разный вид: в задаче о диете требовалось найти минимумцелевой функции, а в задаче о плане производства - максимум. В задаче о диете ограничения имели вид
а в задаче о плане производства - вид
Такой разнобой неудобен при разработке алгоритмов решения этих задач. Поэтому имеются некоторые стандартные формы задач линейного программирования, к которым и приводят конкретные различные задачи. Прежде чем выписывать эти формы, договоримся об обозначениях. Для более краткой записи мы будем использовать векторную или матричную запись. Под векторамимы будем понимать вектора-столбцы, например
Первая стандартная форма задачи линейного программированияимеет вид
Введем вектора
a также вектора
и матрицу
Заметим, что комбинация
Можно использовать и матричные обозначения. Тогда комбинация
Вторая стандартная формазадачи линейного программирования имеет вид
В векторной формеэта задача имеет вид
и в матричной форме -вид
Канонической формой задачи линейного программированияназывается задача вида
В векторной формеэта задача имеет вид
и в матричной форме -вид
Во всех этих задачах функцию
Любой набор чисел Правила приведения задач линейного программирования к стандартной и канонической формам Рассмотрим теперь те приёмы, которые позволяют произвольные формы задач линейного программирования приводить к указанным выше стандартным формам. 1. Превращение мах в min и наоборот. Если целевая функция в задаче линейного программирования задана в виде
то, умножая её на (- 1), приведем её к виду
2. Смена знака неравенства. Если ограничение задано в виде
то, умножая на (- 1), получим:
Аналогично, неравенство вида больше либо равно можно превратить в неравенство вида меньше либо равно . 3. Превращение равенства в систему неравенств. Если ограничение задано в виде
то его можно заменить эквивалентной системой двух неравенств
или такой же системой неравенств со знаками больше либо равно . Указанные выше приемы позволяют приводить задачи линейного программирования к стандартной форме.
4. Превращение неравенств в равенства. Пусть исходная форма задачи линейного программирования имеет вид
Здесь первые r ограничений имеют вид неравенств со знаком меньше либо равно
затем идет группа неравенств со знаком больше либо равно
и, наконец, группа ограничений со знаком = . Для приведения задачи к канонической форме, где все ограничения имеют вид равенств, вводят дополнительные переменные
т.е. в неравенстве со знаком меньше либо равно добавляютдополнительную неотрицательную переменную, а из неравенства со знаком больше либо равно вычитаютдополнительную переменную. В целевую функцию эти дополнительные переменные включают с коэффициентом 0, т.е. фактически они в целевой функции отсутствуют. Получив решение задачи (1.17), т.е. решение задачи в канонической форме, для получения решения исходной задачи (1.16) надо просто выбросить из решения значения введенных дополнительных переменных. Пример Привести к каноническому виду задачу
Введем дополнительные переменные
что и дает эквивалентную задачу в канонической форме. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 и функция этих переменных
и функция этих переменных  , которая носит название целевой функции. Ставится задача: найти экстремум (максимум или минимум) целевой функции
, которая носит название целевой функции. Ставится задача: найти экстремум (максимум или минимум) целевой функции  при условии, что переменные x принадлежат некоторой области G:
при условии, что переменные x принадлежат некоторой области G:
 ;
;
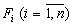 . Предположим, что
. Предположим, что 
 .
.
 . Тогда можно составить таблицу - справочник, указывающую, какое количество каждого компонента имеется в единице веса каждого продукта.
. Тогда можно составить таблицу - справочник, указывающую, какое количество каждого компонента имеется в единице веса каждого продукта.




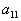


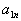
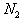





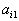





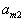


 называется матрицей питательности.
называется матрицей питательности. i-го продукта должно быть скормлено животному за определенный срок (скажем, за месяц). Он означает, что за этот срок животное должно получить единиц первого
i-го продукта должно быть скормлено животному за определенный срок (скажем, за месяц). Он означает, что за этот срок животное должно получить единиц первого 
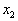

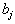 то минимальное количество j-го компонента, которое должно получить животное. Тогда рацион кормления должен удовлетворять ограничениям
то минимальное количество j-го компонента, которое должно получить животное. Тогда рацион кормления должен удовлетворять ограничениям

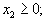




 . Tехнологией производства товара
. Tехнологией производства товара  назовем набор чисел
назовем набор чисел  , показывающий, какое количество i-го ресурса необходимо для производства единицы товара
, показывающий, какое количество i-го ресурса необходимо для производства единицы товара 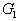








 ,
, .
. ,
,  ,
,



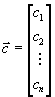 ;
;  ;
; 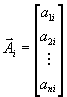 ,
, 
 .
. и
и 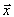 . Поэтому в векторной формезадача (1.7) примет вид
. Поэтому в векторной формезадача (1.7) примет вид


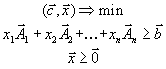
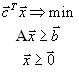



 называют вектором коэффициентовлинейной формы, вектор
называют вектором коэффициентовлинейной формы, вектор  - вектором ограничений.
- вектором ограничений.
 , удовлетворяющий ограничениям задачи, называют планом, а множество всех планов - допустимой областью. Тот план, который доставляет экстремум (минимум или максимум) целевой функции, называют оптимальным планом или просто решением задачи линейного программирования.
, удовлетворяющий ограничениям задачи, называют планом, а множество всех планов - допустимой областью. Тот план, который доставляет экстремум (минимум или максимум) целевой функции, называют оптимальным планом или просто решением задачи линейного программирования. ,
, ,
,
 .
.
 .
. ,
, ,
,



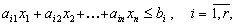

 , которые тоже считаются неотрицательными и записывают исходную задачу в виде
, которые тоже считаются неотрицательными и записывают исходную задачу в виде


 ,
,
 . Переводя мах в min, запишем задачу в виде
. Переводя мах в min, запишем задачу в виде