
|
|
Построение симплекс-таблицыОпределение 4. Задача линейного программирования называется канонической, если она имеет следующий вид. Задача 2. Найти минимум линейной функции:
при ограничениях
или в матричной форме
Определение 5. Мы будем говорить, что задача линейного программирования (1,2) сведена к некоторой канонической задаче линейного программирования (возможно с другим числом переменных и ограничений), если по решению первой задачи можно построить решение второй задачи и наоборот. Пример 4. Свести задачу линейного программирования
при ограничениях
к канонической задаче. Перенесем члены неравенств в одну часть так, чтобы полученные выражения были неотрицательны:
Введем дополнительные переменные
Таким образом, каждому решению Если функция F принимает в некоторой точке максимальное значение, то в этой точке функция (–F) принимает свое минимальное значение. Причем эти значения будут равны с точностью до знака. Таким образом, вместо максимума функции Таким образом, искомая задача может быть сведена к следующей задаче линейного программирования:
при ограничениях
По оптимальному решению первоначальной задачи легко найти оптимальное решение канонической задачи. Минимальное значение функции
Определение 6. Набор из m различных переменных системы уравнений (7) называется базисным, если все переменные из этого набора могут быть выражены только через оставшиеся переменные с помощью элементарных преобразований системы. Переменные, входящие в этот набор, называются базисными, а остальные свободными. Определение 7. Решение системы (7) называется базисным (опорным планом), если значения всех свободных переменных равны нулю. Пример 5. Найти базисное решение системы:
Решение. В этой системе уравнений за базисные переменные можно взять переменные Определение 8. Симплекс-таблицей для канонической задачи (6), (7) называется следующая таблица: Таблица 1
Здесь Мы будем называть эту таблицу базисной, если в столбцах помеченных переменными В дальнейшем мы будем иметь дело только с базисными симплекс-таблицами. Каждая базисная симплекс-таблица порождает некоторое базисное решение. В нем значения выделенных базисных переменных равны соответствующим свободным членам, а значения остальных переменных равны нулю. Легко убедиться в верности следующих условий допустимости и оптимальности базисных решений Условие допустимости. Базисное решение, порождаемое базисной симплекс-таблицей, допустимо, если все элементы столбца свободных членов неотрицательны: Условие оптимальности. Допустимое базисное решение, порождаемое базисной симплекс таблицей, оптимально, если все числа, стоящие в последней строке, неположительные, за исключением, быть может, числа Таким образом, мы выделили класс симплекс-таблиц, по которым легко построить оптимальное базисное решение. Пример 6. Записать следующую задачу в форме симплекс таблицы в базисе переменных
Решение. Соответствующая симплекс таблица будет иметь вид: Таблица 2
Базисным решением задачи будет матрица 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 , (6)
, (6) (7)
(7)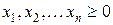 ,
, , (8)
, (8) ,
,  . (9)
. (9)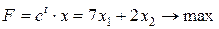 ,
, (10)
(10)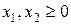 ,
,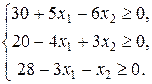
 ,
, 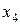 ,
,  по формулам:
по формулам: (11)
(11) системы неравенств (10) будет соответствовать решение
системы неравенств (10) будет соответствовать решение  системы уравнений (11), причем все его компоненты будут неотрицательны. И наоборот каждому неотрицательному решению
системы уравнений (11), причем все его компоненты будут неотрицательны. И наоборот каждому неотрицательному решению  на множестве D можно искать на этом множестве минимум функции
на множестве D можно искать на этом множестве минимум функции  .
. ,
,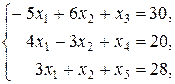
 .
. , в точке с координатами:
, в точке с координатами: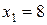 ,
,  ,
,  ,
,  ,
,  .
.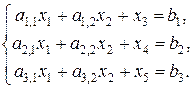 (12)
(12) , а за свободные
, а за свободные  , так как первые легко выражаются через последние. Итак, базисным решением этой системы будет набор чисел
, так как первые легко выражаются через последние. Итак, базисным решением этой системы будет набор чисел  .
.













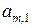







 имена базисных переменных. Последняя строка таблицы соответствует равенству
имена базисных переменных. Последняя строка таблицы соответствует равенству  .
. ,
,  .
. при ограничениях (12) и
при ограничениях (12) и  .
.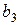
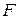
 . Оно будет допустимым, если
. Оно будет допустимым, если  и оптимальным, если
и оптимальным, если  . При выполнении этих условий минимальное значение функции F будет равно
. При выполнении этих условий минимальное значение функции F будет равно