
|
|
ПРИМЕР 1. ЗАДАЧА О ВЫПУСКЕ ПРОДУКЦИИ.12 Детерминированные методы. ЛАБОРАТОРНАЯ РАБОТА № 2. Линейное программирование. Цель работы: исследование применения количественных методов в управлении, когда требуется максимизировать (минимизировать) заданную целевую функцию при некоторых ограничениях. ЛИНЕЙНЫЕ ЗАДАЧИ. В зависимости от вида ограничений и целевой функции выделяют задачи линейного, квадратичного, выпуклого программирования, для решения последних применяется довольно сложный математический аппарат. В данной лабораторной работе рассматриваются линейные модели как одни из наиболее активно используемых классов математических моделей. Такие модели сравнительно просты, хорошо формализованы, допускают полное исследование и достаточно эффективны в целом ряде стандартных ситуаций. Линейность – это свойство математических выражений и функций. Выражение вида
где xи y– переменные величины, а aи b– постоянные числа, называется линейным относительно переменных x и y. В случае если переменных больше двух – х1, х2, …, хn, линейное выражение относительно этих переменных имеет вид где а1, а2, …, аn– постоянные числа. Линейное программирование является наиболее известным и одним из наиболее широко используемых инструментов науки управления /management science/. Это математический метод решения задачи оптимального распределения имеющихся ресурсов (денег, материалов, времени) для достижения определённой цели (наибольшего дохода или наименьших затрат). Программирование в данном контексте имеет смысл планирования. Линейноеже означает, что ищется экстремум линейной целевой функции при линейных ограничениях (линейных уравнениях или неравенствах). Таким образом, линейное программирование имеет мало общего с программированием, используемым в computer science, однако, вычислительные средства играют существенную роль в повышении эффективности его приложений. Ниже приводятся несколько общих ситуаций, в которых линейное программирование применяется часто и эффективно: задачи о составлении смеси, цель которых заключается в выборе наиболее экономичной смеси ингредиентов (газа, нефти, пищевых продуктах) при учёте ограничений на физический или химический состав смеси и на наличие необходимых материалов; задачи производства, целью которых является подбор наиболее выгодной производственной программы выпуска одного или нескольких видов продукции при использовании некоторого числа ограниченных источников сырья; задачи распределения, цель которых состоит в том, чтобы организовать доставку материалов от некоторого числа источников к некоторому числу потребителей так, чтобы оказались минимальными либо расходы по этой доставке, либо время, затраченное на неё, либо некоторая комбинация того и другого. В простейшем виде это задача о перевозках (транспортная задача). Наиболее распространённым методом решения задач линейного программирования является так называемый симплекс – метод, а наиболее эффективным из известных – метод эллипсоидов. В простейшем случае удобен простой и наглядный графический метод. Если задача сводится к системе линейных уравнений, то наиболее простым и эффективным подходом к решению линейных систем является метод последовательного исключения неизвестной. ОБЩАЯ ЗАДАЧА ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ Стандартная математическая формулировка общей задачи линейного программирования выглядит так:
требуется найти экстремальное значение показателя эффективности (целевой функции) (линейной функции элементов решения х1, х2, …, хn) при линейных ограничительных условиях, накладываемых на элементы решения:
………………………………………………………..
где aik, bk, ai –заданные числа.
Или в соответствии с правилом сокращённого суммирования запись общей задачи линейного программирования выглядит таким образом:
xk ≥ 0, k = 1, 2, …,n.
ПРИМЕР 1. ЗАДАЧА О ВЫПУСКЕ ПРОДУКЦИИ. Фирма выпускает два вида древесно – стружечных плит – обычные и улучшенные. При этом производятся две основные операции – прессование и отделка. Требуется определить, какое количество плит каждого типа можно изготовить в течение месяца так, чтобы обеспечить максимальную прибыль при ограничениях на ресурсы (материал, время, затраты), указанных в табл.1, если за каждые 100 обычных плит фирма получает прибыль, равную 80 ?, а за каждые 100 плит улучшенного вида 100 ?. Таблица 1.
Перейдём к построению математической модели поставленной задачи. Введём следующие обозначения. Пусть х –количество партий в 100 плит обычного вида, изготавливаемых в течение месяца, y– то же для плит улучшенного качества. Тогда ожидаемую прибыль можно записать так:
Ограничения на материал формируются по следующим соображениям. Для изготовления х партий в 100 плит обычного вида и y партий в 100 плит улучшенного вида требуется
фунтов дерева. Ясно, что полученное число не может превосходить количество материала, имеющегося в наличии, т.е. 4000 фунтов. Подобным же образом рассчитываются ограничения на время изготовления и затраты: прессование: отделка: затраты: Подведём итог. Требуется найти такие значения х и y, подчинённые условиям:
для которых
(2) Для решения поставленной задачи используем графический метод. На плоскости OXY рассмотрим полуплоскости, ограниченные неравенствами (1). Пересечением полученных полуплоскостей будет четырехугольник, при этом целевая функция (2) достигает наибольшего значения в одной из вершин этого четырёхугольника.
Цель задачи заключается в минимизации полной стоимости перевозок известного количества товаров со складов к потребителю. Причём речь идёт о так называемой сбалансированной транспортной задаче, в которой общий объём товаров, готовых к отправлению, в точности равен объёму товаров, который готовы принять в пунктах назначения. Компания имеет два товарных склада и трёх оптовых покупателей. Известно, что общий объём запасов на складах составляет 300 тыс. единиц продукции и совпадает с общим объёмом заказов покупателей. Конкретные данные о загруженности каждого из складов (в тыс. единиц), потребности каждого покупателя (в тыс. единиц) и стоимости перевозки (млн. руб за 1 тыс. ед.) приведены в табл.2. Таблица 2.
  Обозначим через хikколичество товара, поставляемого со склада Ai покупателю Bk (рис.1). Обозначим через хikколичество товара, поставляемого со склада Ai покупателю Bk (рис.1).
Рис.1 Тогда необходимо минимизировать общую стоимость перевозок:
при условии, что
Получаем задачу линейного программирования, в которой основные ограничения вследствие того, что транспортная задача сбалансирована, являются равенствами. Задача на рис.2 представлена сетью.
Рис.2.
Положим, что х11 = u, х12 = v и выразим через u и v остальные переменные, которые затем подставим в целевую функцию (3). Имеем :
Учитывая, что все хik неотрицательны, мы приходим к задаче, которая решается графическим методом:
В ходе решения задачи получаем, что х11= 0, х12= 120, х13= 0, х21=70, х22= 20, х23=90, zmin=1690.

12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 ,
, ,
,
 ,
, ,
,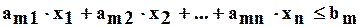 ,
, ,
,  , …….,
, …….,  ,
, ,
, , i = 1, 2, …., m,
, i = 1, 2, …., m,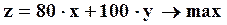

 ,
, ,
, .
.
 ,
, ,
,
 Полученное решение ZM =13000, X=100, Y=50
Полученное решение ZM =13000, X=100, Y=50
 2.2.2. ПРИМЕР 2. ТРАНСПОРТНАЯ ЗАДАЧА.
2.2.2. ПРИМЕР 2. ТРАНСПОРТНАЯ ЗАДАЧА.
 (3)
(3)
 ,
, ,
, ,
, , (4)
, (4) ,
, ,
,  ,
,  ,
, ,
, 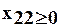 ,
,  .
.

 .
.
 ,
, ,
, ,
, ,
, ,
,  ,
, .
.