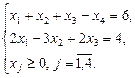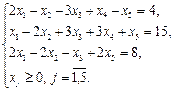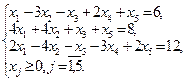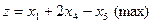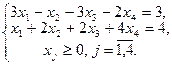|
|
Двойственность в задачах линейного программированияС каждой задачей линейного программирования тесно связана другая линейная задача, называемая двойственной; первоначальная задача называется исходной или прямой.
Две приведенные задачи образуют двойственную пару. Двойственная задача по отношению к исходной составляется согласно следующим правилам: 1) целевая функция исходной задачи формулируется на максимум, а целевая функция двойственной задачи — на минимум, при этом в задаче на максимум все неравенства в функциональных ограничениях имеют вид "£", в задаче на минимум — вид "³"; 2) матрица А, составленная из коэффициентов при неизвестных в системе ограничений исходной задачи и аналогичная матрица Ат в двойственной задаче получаются друг из друга транспонированием; 3) число переменных в двойственной задаче равно числу функциональных ограничений исходной задачи, а число ограничений в системе двойственной задачи — числу переменных в исходной задаче; 4) коэффициентами при неизвестных в целевой функции двойственной задачи являются свободные члены в системе ограничений исходной задачи, а правыми частями в ограничениях двойственной задачи — коэффициенты при неизвестных в целевой функции исходной задачи; 5) если переменная xj исходной задачи может принимать только положительные значения, то j-ое условие в системе ограничений двойственной задачи является неравенством вида "≥". Если же переменная может принимать как положительные, так и отрицательные значения, то j-ое условие представляет собой уравнение. И наоборот, если i-ое соотношение в системе ограничений исходной задачи является неравенством, то i-ая переменная двойственной задачи yi ≥0. В противном случае переменная yi может принимать как положительные, так и отрицательные значения. В теории двойственности используются четыре пары двойственных задач (приведем их в матричнойформе записи):
Первая теорема двойственности. Если одна из пары двойственных задач имеет оптимальный план, то и другая имеет оптимальный план и значения целевых функций задач при их оптимальных планах равны между собой, т. е. Если же целевая функция одной из пары двойственных задач не ограничена (для исходной – сверху, для двойственной – снизу), то другая задача вообще не имеет планов. Вторая теорема двойственности. План Если в оптимальном плане одной из задач соответствующая переменная отлична от нуля, то ограничение другой задачи в оптимальном плане выполняются в виде равенства. Если в оптимальном плане одной из задач какое-либо ограничение выполняется в виде строгого неравенства, то соответствующая переменная другой задачи в оптимальном плане равна нулю. Эти условия позволяют, зная оптимальное решение одной из взаимно двойственных задач, найти оптимальное решение другой задачи.
Пример.Решить задачу линейного программирования симплексным методом. Составить для данной задачи линейного программирования двойственную задачу и по решению прямой задачи найти решение двойственной, используя теоремы двойственности.
Приведем задачу к каноническому виду. Для этого к левой часть первого неравенства прибавим дополнительную неотрицательную переменную
Преобразованную систему уравнений запишем в векторной форме:
где Среди векторов P1, P2, P3, P4, P5, только два единичных вектора (P3 и P4), т.е. единичного базиса нет. Поэтому составим расширенную задачу. Для этого в левую часть третьего уравнения системы ограничений добавим искусственную переменную Составим симплексную таблицу для I итерации:
Вычислим оценки разложений векторов по базису опорного решения по формуле
Оценки векторов, входящих в базис, всегда равны нулю. Значение F0 равно скалярному произведению вектора P0 на вектор Сб: F0=1*0+8*0+3*(-М) = -3М. Значения F0 и Начальное опорное решение не является оптимальным, так как в 5-й строкеимеется два отрицательных числа Далее выполним преобразование Жордана с разрешающим элементом Получим симплексную таблицу для II итерации:
Она содержит только четыре строки, так как искусственный вектор из базиса исключён и оценки больше не содержат слагаемого с М. Этот вектор не имеет смысла вводить ни в один из последующих базисов, поэтому в дальнейшем столбец данного вектора можно не заполнять. Но так как от нас требуется найти решение двойственно задачи, то мы его оставим. Получили новый опорный план Рассмотрим элементы 4-й строки. В столбце векторов
Последняя строка снова содержит отрицательное число. В базис вводим вектор
В 4-й строке последней симплексной таблицы нет отрицательных чисел. Значит, найденный опорный план
Составим двойственную задачу. Умножим третье ограничение на -1, тогда все неравенства будут содержать знак «≤». Задача примет вид исходной задачи симметричной пары 1 (см. выше):
Число переменных в двойственной задаче равно числу ограничений в исходной задаче, т.е. трём: Умножим правые части ограничений на соответствующие переменные двойственной задачи и сложим их, получим целевую функцию: Целевая функция исходной задачи исследуется на максимум, следовательно, целевая функция двойственной задачи исследуется на минимум. Матрица системы ограничений исходной задачи имеет вид: Окончательно двойственная задача имеет следующий вид:
Найдём её решение, используя теоремы двойственности. По первой теореме двойственности оптимальные решения исходной и двойственной задач равны, следовательно, Из соотношений второй теоремы двойственности следует, что если в оптимальном плане исходной задачи какое-то ограничение выполняется в виде строгого неравенства, то соответствующая двойственная оценка равна нулю. Подставим найденное оптимальное решение в систему ограничений исходной задачи:
Третье ограничение выполняется в виде строгого неравенства, следовательно, Если некоторая компонента
Решив систему, получим Окончательно Решение двойственной задачи можно получить другим способом, используя формулу Матрица
Ответ:
Транспортная задача
Пусть имеется m поставщиков А1, А2, ..., Аm однородного груза в количествах соответственно а1, а2, .., .аm единиц и n потребителей В1, В2, ..., Вn этого груза, потребность которых составляет соответственно b1, b2 ..., bn единиц. Известны стоимости перевозок (тариф) единицы груза от i-го поставщика к j-му потребителю - сij (i=1,m; j=1,n). Требуется составить такой план перевозок, который обеспечит минимальные транспортные расходы. Возможны три ситуации: 1) количество груза у всех поставщиков равно потребности в данном грузе всех потребителей:
2) количество груза у всех поставщиков больше потребности в данном грузе всех потребителей:
3) количество груза у всех поставщиков меньше потребности в данном грузе всех потребителей:
В первом случае модель задачи называется закрытой, во втором и третьем – открытой. Теорема.Для разрешимости транспортной задачи необходимо и достаточно, чтобы запасы груза в пунктах отправления были равны потребностям в грузе в пунктах назначения, т. е. чтобы выполнялось равенство В случае превышения запаса над потребностью вводится фиктивный (n + 1)-й пункт назначения с потребностью Аналогично вводится фиктивный (m + 1)-й пункт отправления с запасом груза Решение транспортной задачи включает следующие этапы: 1. Нахождение первоначального опорного плана (метод северо-западного угла, метод минимальной стоимости). При этом число заполненных клеток должно быть равно m + n - 1. При нахождении опорного плана методом северо-западного угла запасы очередного поставщика используются для обеспечения запросов очередных потребителей до тех пор, пока не будут исчерпаны полностью, после чего используются запасы следующего по номеру поставщика. Заполнение начинается с левой верхней клетки (северо-западный угол). На каждом шаге, исходя из запасов очередного поставщика и запросов очередного потребителя, заполняется только одна клетка и исключается из рассмотрения один поставщик или потребитель. Если в очередную клетку таблицы требуется поставить перевозку, а поставщик или потребитель имеют нулевые запасы или запросы, то в клетку ставится перевозка, равная нулю (базисный нуль), и после этого исключается из рассмотрения поставщик или потребитель. Метод минимальной стоимости позволяет построить решение, близкое к оптимальному, так как использует матрицу стоимостей транспортной задачи. На каждом шаге заполняется только одна клетка, соответствующая минимальной стоимости, и исключается из рассмотрения только один поставщик или один потребитель. Очередную клетку, соответствующую минимальной стоимости, заполняют по тем же правилам, что и в методе северо-западного угла. Поставщик исключается из рассмотрения, если его запасы исчерпаны полностью. Потребитель исключается из рассмотрения, если его запросы удовлетворены полностью. При этом если поставщик еще не исключен, но его запасы равны нулю, то на том шаге, когда от поставщика требуется поставить груз, в соответствующую клетку таблицы заносится базисный нуль и лишь затем поставщик исключается из рассмотрения. 2. Проверка опорного плана на оптимальность, например, методом потенциалов.
Пример.Четыре предприятия используют три вида сырья. Потребности в сырье каждого из предприятий соответственно равны 100, 90, 170 и 30 ед. Сырьё сосредоточено в трёх пунктах, а запасы соответственно равны 200, 160, и 140 ед. Тарифы перевозок заданы матрицей
Составить такой план перевозок, при котором общая стоимость перевозок является минимальной. Данная задача является открытой, так как потребности в сырье 100+90+170+30=390 меньше запасов 200+160+140=500. Введём 5-го фиктивного потребителя с потребностью Теперь исходные данные задачи запишем в виде таблицы, а опорный план получим методом северо-западного угла. Заполнение таблицы начинаем с клетки (1, 1). х11 = min(a1=200,b1=100)=b1=100 – запасы А1 позволяют полностью удовлетворить потребности пункта В1, значит исключаем этого потребителя из рассмотрения. Теперь запасы пункта A1 считаем равными a1=200 - 100=100 ед. В оставшейся части таблицы левой верхней клеткой является (1, 2): х12= min(a1, b2)=b2=90 – снова запасы удовлетворяют потребность полностью. Внесём значение в соответствующую клетку и исключим из рассмотрения столбец В2. Запасы пункта А1 считаем равными a1 = 100 – 90 = 10 ед. Теперь «северо-западным углом» является клетка (1, 3). х13 = min(a1, b3)= a1 =10 – запасы могут удовлетворить потребность пункта B3 частично. Заполняем клетку (1, 3) и исключаем из рассмотрения строку A1. Потребности пункта B3 считаем равными b3 = 170 - 10 = 160. х23 = min(a2, b3) = a2 = b3 = 160 – запасы A2 исчерпаны, потребность B3 удовлетворена. Но по правилам мы не можем вычеркнуть и строку и столбец одновременно. Поэтому исключим из рассмотрения сначала столбец B3, а в клетку (2, 4) запишем х24 = 0 (так как запасы А2 уже исчерпаны) и только теперь вычеркнем строку А2. И так далее. Получим следующую таблицу.
Число заполненных клеток равно 7 и m + n - 1=3 + 5 – 1 = 7 – план невырожденный. Оптимальный план найдём методом потенциалов. Теорема. В оптимальном плане транспортной задачи заполненным клеткам отвечают равенства Расставим потенциалы:
(Обычно равным нулю принимают потенциал строки или столбца с наибольшим числом заполненных клеток.) Теперь проверим пустые клетки на выполнение неравенства
Для клеток (1, 4), (1, 5), (2, 2) неравенство не выполняется, значит опорный план не является оптимальным. В одну из этих клеток нужно "ввезти" груз. Выбираем ту, для которой разница Цикл перерасчёта таблицы - это последовательность ячеек, начинающаяся и заканчивающаяся в одной и той же клетке, с вершинами, лежащими в занятых клетках, кроме одной. Вершина цикла – клетка, в которой происходит поворот под прямым углом. "Перемещаем" груз по следующим правилам: 1. каждой из клеток, связанных циклом присваивается знак: пустой ячейке "+", остальным - поочерёдно знаки "-" и "+" . 2. среди минусовых клеток находим число В нашем примере цикл образуют шесть ячеек: (1, 5) – пустая, для которой не выполняется неравенство, и (3, 5), (3, 4), (2, 4), (2, 3), (1, 3) – заполненные.
х = min(10,0,110)=0. Значит в плюсовые клетки "завозим" 0 ед. груза, из минусовых "вывозим". Получим новый опорный план:
Расставим потенциалы и проверим пустые клетки на выполнение неравенства
х = min(90,160)=90. Значит в плюсовые клетки "завозим" 90 ед. груза, из минусовых "вывозим". Получим новый опорный план:
Расставим потенциалы и проверим пустые клетки на выполнение неравенства Ответ:
Так как пятый потребитель является фиктивным, то 110 ед. груза у третьего поставщика останутся невостребованными. Задачи для самостоятельного решения
Задание 1 1) Привести задачу линейного программирования к стандартной форме; 2) решить задачу графически.
Задание 2 Составить экономико-математическую модель. 1.В плановом году строительные организации города переходят к сооружению домов типов Д-1, Д-2, Д-3 и Д-4. Данные о количестве квартир разного типа в каждом из указанных типов домов, их плановая себестоимость приведены в таблице. Годовой план ввода жилой площади составляет соответственно 800, 1000, 900, 2000 и 7000 квартир указанных типов.
Исходя из необходимости выполнения плана ввода квартир (возможно его перевыполнения по всем показателям) и обеспеченности строительными материалами и трудовыми ресурсами, построить модель и сформулировать на ее основе экстремальную задачу нахождения плана строительства, при котором себестоимость всех вводимых домов будет минимальной. 2.Фабрика производит два вида красок: первый – для наружных, а второй – для внутренних работ. Для производства красок используются два ингредиента: А и В. Максимально возможные суточные запасы этих ингредиентов составляют 6 и 8 т соответственно. Известны расходы А и В на 1 т соответствующих красок (таблица). Изучение рынка сбыта показало, что суточный спрос на краску 2-го вида никогда не превышает спроса на краску 1-го вида более, чем на 1 т. Кроме того, установлено, что спрос на краску 2-го вида никогда не превышает 2 т в сутки. Оптовые цены одной тонны красок равны: 3 тыс. руб. для краски 1-го вида; 2 тыс. руб. для краски 2-го вида. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|




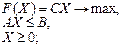







 .
. исходной задачи и план
исходной задачи и план  двойственной задачи являются оптимальными планами этих задач тогда и только тогда, когда для любых i и j выполняются равенства:
двойственной задачи являются оптимальными планами этих задач тогда и только тогда, когда для любых i и j выполняются равенства:


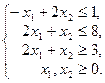
 , к левой части второго -
, к левой части второго -  . А вот из левой части третьего неравенства вычтем переменную
. А вот из левой части третьего неравенства вычтем переменную  . В целевую функцию каждая из этих переменных входит с коэффициентом 0 (т. е. не входят). Получаем
. В целевую функцию каждая из этих переменных входит с коэффициентом 0 (т. е. не входят). Получаем
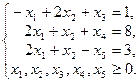
 ,
, ;
;  ;
;  ;
;  ;
;  ;
;  .
. . Её нужно как можно быстрее вывести из базиса. Поэтому в целевую функцию в задаче максимизации новая переменная войдёт с очень большим отрицательным коэффициентом –М. Расширенная задача имеет опорный план
. Её нужно как можно быстрее вывести из базиса. Поэтому в целевую функцию в задаче максимизации новая переменная войдёт с очень большим отрицательным коэффициентом –М. Расширенная задача имеет опорный план  , определяемый системой трёх единичных векторов:
, определяемый системой трёх единичных векторов: 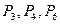 .
.









 , где zj находится как скалярное произведение вектора Pj (j=1,m) на вектор Сб=(с1, с2, ...,сm):
, где zj находится как скалярное произведение вектора Pj (j=1,m) на вектор Сб=(с1, с2, ...,сm):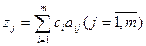 .
.
 состоят из двух слагаемых
состоят из двух слагаемых  . Слагаемое, которое не содержит М, записываем в 4-й строке, а число, стоящее при М – в 5-й.
. Слагаемое, которое не содержит М, записываем в 4-й строке, а число, стоящее при М – в 5-й. и
и  . Для оптимальности опорного решения в задаче на максимум требуется неотрицательность оценок для всех векторов. Чтобы перейти к новому опорному решению в базис можно ввести любой из векторов P1 и P2. Выберем P1, так как ему соответствует наибольшая по модулю оценка. Для определения вектора, подлежащего выводу из базиса, находят
. Для оптимальности опорного решения в задаче на максимум требуется неотрицательность оценок для всех векторов. Чтобы перейти к новому опорному решению в базис можно ввести любой из векторов P1 и P2. Выберем P1, так как ему соответствует наибольшая по модулю оценка. Для определения вектора, подлежащего выводу из базиса, находят  для всех aij>0. Для вектора P1получим
для всех aij>0. Для вектора P1получим  (
(  , поэтому отношение
, поэтому отношение  не рассматриваем). Минимум достигается при i=3. В третьей строке столбца «Базис» находится вектор Р6. Следовательно, его из базиса исключаем.
не рассматриваем). Минимум достигается при i=3. В третьей строке столбца «Базис» находится вектор Р6. Следовательно, его из базиса исключаем. =2: 1) разделим всю третью строку на 2 и запишем результат в новую симплексную таблицу; 2) остальные элементы первого столбца нужно занулить, для этого полученную 3-ю строку сложим с первой, результат запишем в первую строку новой симплексной таблицы; 3) умножим новую 3-ю строку на -2 (или прежнюю на -1) и сложим со второй строкой, результат запишем во вторую строку новой симплексной таблицы.
=2: 1) разделим всю третью строку на 2 и запишем результат в новую симплексную таблицу; 2) остальные элементы первого столбца нужно занулить, для этого полученную 3-ю строку сложим с первой, результат запишем в первую строку новой симплексной таблицы; 3) умножим новую 3-ю строку на -2 (или прежнюю на -1) и сложим со второй строкой, результат запишем во вторую строку новой симплексной таблицы.

 и значение целевой функции F0 = 3.
и значение целевой функции F0 = 3.
 является оптимальным. Значение целевой функции
является оптимальным. Значение целевой функции 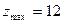 .
.
 .
.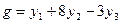 .
. . Транспонируем её и получим аналогичную матрицу двойственной задачи -
. Транспонируем её и получим аналогичную матрицу двойственной задачи -  . Так как в исходной задаче обе переменные неотрицательные, то оба ограничения двойственной задачи будут являться неравенствами. правыми частями в ограничениях двойственной задачи являются коэффициенты при неизвестных в целевой функции исходной задачи. И так как все три ограничения исходной задачи являются неравенствами, то все три переменные двойственной задачи будут неотрицательными.
. Так как в исходной задаче обе переменные неотрицательные, то оба ограничения двойственной задачи будут являться неравенствами. правыми частями в ограничениях двойственной задачи являются коэффициенты при неизвестных в целевой функции исходной задачи. И так как все три ограничения исходной задачи являются неравенствами, то все три переменные двойственной задачи будут неотрицательными. .
.
 .
.
 .
. оптимального плана исходной задачи отлична от нуля, то соответствующее ограничение двойственной задачи выполняется в виде равенства. В нашем примере и
оптимального плана исходной задачи отлична от нуля, то соответствующее ограничение двойственной задачи выполняется в виде равенства. В нашем примере и  , и
, и  , следовательно, оба ограничения двойственной задачи выполняются в виде равенства.
, следовательно, оба ограничения двойственной задачи выполняются в виде равенства. Учитывая, что
Учитывая, что 


 .
. находится в последней симплексной таблице. Ее столбцы расположены под столбцами единичной матрицы, образующими базис начального опорного решения, т. е. под векторами
находится в последней симплексной таблице. Ее столбцы расположены под столбцами единичной матрицы, образующими базис начального опорного решения, т. е. под векторами 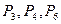 (именно для этой цели мы продолжали вычислять вектор
(именно для этой цели мы продолжали вычислять вектор 
 ,
,  или
или 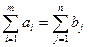 .
. или
или  .
.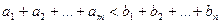 или
или  .
. и соответствующие тарифы считаются равными нулю.
и соответствующие тарифы считаются равными нулю. и тарифы полагаются равными нулю. Этим задача сводится к закрытой транспортной задаче, из оптимального плана которой получается оптимальный план исходной задачи.
и тарифы полагаются равными нулю. Этим задача сводится к закрытой транспортной задаче, из оптимального плана которой получается оптимальный план исходной задачи. .
. .
. , а пустым неравенства
, а пустым неравенства  .
. , положим
, положим  , тогда
, тогда  .
. .
. максимальна, т. е. в (1, 5). Строим цикл.
максимальна, т. е. в (1, 5). Строим цикл. и прибавляем его к числам, стоящим в плюсовых клетках, и вычитаем из чисел, стоящих в минусовых клетках; остальные клетки вне цикла остаются без изменения.
и прибавляем его к числам, стоящим в плюсовых клетках, и вычитаем из чисел, стоящих в минусовых клетках; остальные клетки вне цикла остаются без изменения.

 ,
, =100*12+100*21+90*8+70*15+30*12=5430.
=100*12+100*21+90*8+70*15+30*12=5430.