
|
|
РАСЧЁТНО-ПОЯСНИТЕЛЬНАЯ ЗАПИСКАУО «Гродненский государственный политехнический колледж» Специальность: 2-530105 «Автоматизированные электроприводы». Специализация: 2-520105.01 «Автоматизированные электроприводы промышленных и транспортных установок».
КУРСОВАЯ РАБОТА По предмету: «Теоретические основы электротехники» Расчёт и анализ электрических цепей
РАСЧЁТНО-ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Выполнил: учащийся гр. АЭП-1.10 Купцевич А.А. Проверил: Торяник Ю.П.
СОДЕРЖАНИЕ
Введение.......................................................................................................... 4 1. Анализ электрического состояния линейных и нелинейных электрических цепей постоянного тока........................................................... 5 1.1. Расчет линейных электрических цепей постоянного тока............. 5 1.2. Расчет нелинейных электрических цепей постоянного тока....... 22 2. Анализ электрического состояния линейных электрических цепей переменного тока: однофазных и трехфазных............................................... 25 2.1. Расчет однофазных линейных электрических цепей переменного тока................................................................................ 25 2.2. Расчет трехфазных линейных электрических цепей переменного тока................................................................................ 31 3. Исследование переходных процессов в электрических цепях............... 37 Заключение................................................................................................... 42 Литература................................................................................................... 43
Электротехника – это область науки и техники, которая занимается изучением электрических и магнитных явлений и их использованием в практических целях. Можно выделить три основных направления электротехники: 1) преобразование различных видов энергии природы в электрическую энергию; 2) превращение одних веществ природы в другие; 3) получение и передача информации. Научно-технический процесс не возможен без электрификации всех отраслей народного хозяйства. Потребности народного хозяйства в электрической энергии непрерывно растут, что и приводит к увеличению её производства. В условиях научно-технической революции особенно отчётливо проявилась глубокая связь науки, техники и производства. Наука стала непосредственной производительной силой, а научные достижения оказались в существенной степени зависящими от уровня развития и возможностей современных технологий. Предполагаемая курсовая работа имеет цель научить решать некоторые типы задач по электротехнике и строить некоторые графики по решению этих задач.
1.1 Расчёт линейных электрических цепей постоянного тока. Для электрической цепи изображенной на рисунке 1,
Дано: Е1=20 В, Е2=30 В, R1=54 Ом, R2=43 Ом , R3=32 Ом, R4=26 Ом, R5=51 Ом, R6=15 Ом, r01=2 Ом, r02=2 Ом.
Определить: I1, I2, I3, I4, I5, I6.
Выполнить следующее: 1) составить на основании законов Кирхгофа систему уравнений для определения токов во всех ветвях схемы; 2) определить токи во всех ветвях схемы, используя метод контурных токов; 3) определить токи во всех ветвях схемы на основании метода наложения; 4) составить баланс мощностей для заданной схемы; 5) результаты расчётов токов по пунктам 1, 2 и 3 занести в таблицу; 6) определить ток во второй ветви методом эквивалентного генератора; 7) построить потенциальную диаграмму для любого замкнутого контура;
1.1.1 Составить на основании законов Кирхгофа систему уравнений для определения токов во всех ветвях.
При расчёте данным методом произвольно задаём направление токов в ветвях I1, I2, I3, I4, I5 и I6. Составляем систему уравнений. В системе должно быть столько уравнений, сколько в цепи ветвей (неизвестных токов). В заданной цепи шесть ветвей, значит, в системе должно быть шесть уравнений (m=6). Сначала составляем уравнения для узлов по первому закону Кирхгофа. Для цепи с n узлами можно составить (n-1) независимых уравнений. В нашей цепи четыре узла (А, В, С и D), значит, число уравнений: узел B: узел A: узел D: Всего в системе должно быть шесть уравнений. Три уже есть. Три недостающих составляем для линейно независимых контуров. Чтобы они были независимыми, в каждый следующий контур необходимо включить хотя бы одну ветвь, не входящую в предыдущие. Задаёмся обходом каждого контура и составляем уравнения по второму закону Кирхгофа. Контур ABCA – обход по часовой стрелке:
Контур BCDB – обход по часовой стрелке:
Контур ABDA – обход по часовой стрелке:
ЭДС в контуре берётся со знаком «+», если направление ЭДС совпадает с обходом контура, если не совпадает – знак «–».
совпадает. Мы получили систему из шести уравнений с шестью неизвестными.
Подставив уравнения, полученные по первому закону Кирхгофа, в последние три мы получим систему из трёх уравнений с тремя неизвестными:
Раскроем скобки и приведём подобные слагаемые:
Подставим численные значения ЭДС источников и сопротивлений:
Решив данную систему с помощью, определим величину и направление тока во всех ветвях схемы. Вычислим определители Δ, Δ1, Δ2, Δ3.
Вычисляем токи:
По закону Кирхгофа для узла, найдём недостающие токи:
1.1.2 Определить токи во всех ветвях схемы (рисунок 1), используя метод контурных токов. Метод контурных токов основан на использовании только второго закона Кирхгофа. Это позволяет уменьшить число уравнений в системе на Достигается это разделением схемы на ячейки (независимые контуры) и введением для каждого контура-ячейки своего тока – контурного тока, являющегося расчётной величиной. Итак, в заданной цепи (рисунок 2) можно рассмотреть три контура ячейки (ABDA, ACBA и ACDBA) и ввести для них контурные токи Ik1, Ik2 и Ik3. Контуры-ячейки имеют ветвь, не входящую в другие контуры – это внешние ветви. В этих ветвях контурные токи являются действительными токами ветвей. Ветви, принадлежащие двум смежными контурам, называются смежными ветвями. В них действительный ток равен алгебраической сумме контурных токов смежных контуров, с учётом их направления. При составлении уравнений по второму закону Кирхгофа в левой части равенства алгебраически суммируются ЭДС источников, входящих в контур-ячейку, в правой части равенства алгебраически суммируются напряжения на сопротивлениях, входящих в этот контур, а также учитывается падение напряжения на сопротивлениях смежной ветви, определяемая по контурному току соседнего контура.
- стрелками указываем выбранное направление контурных токов Ik1, Ik2, Ik3 в контурах-ячейках. Направление обхода контуров принимаем таким же: - составляем уравнения и решаем систему из этих уравнений с помощью определителей.
Подставим численные значения сопротивлений и ЭДС источников.
или
Решаем данную систему через определители. Для нахождения токов рассчитаем определители Δ, Δ1, Δ2, Δ3.
Вычисляем контурные токи:
Найдём действительные токи:
Если при решении системы ток получается со знаком «–», значит его действительное направление обратно направлению соответствующего контурного тока.
1.1.3 Определить токи во всех ветвях схемы на основании метода наложения.
а) Определяем частные токи от ЭДС Е1 при отсутствии Е2, то есть рассматриваем цепь изображенную на рисунке 3. Показываем направление частных токов от ЭДС Е1 и обозначаем буквой I с одним штрихом (I¢). Решаем задачу методам «свертывания».
Чтобы «свернуть» схему нам необходимо преобразовать звезду с сопротивлениями R2,02; R4; R6 в треугольник с сопротивлениями RA, RB, RC (рисунок 4).
Сопротивления треугольника определяются по формулам:
Продолжаем «сворачивать» схему:
Эквивалентное сопротивление схемы:
Ток источника ЭДС E1 равен:
Найдём общий ток в ветви BD (используя формулу разброса):
Зная ток ветви BD найдём токи I3¢ и I5¢:
Оставшиеся токи найдём по первому закону Кирхгофа:
б) Определяем частные токи от ЭДС Е2 при отсутствии Е1, т.е. рассчитываем простую цепь (рисунок 5).
Показываем направление частных токов от ЭДС Е2 и обозначаем их буквой I с двумя штрихами (I²). «Сворачиваем» схему.
Продолжаем «сворачивать» схему:
Эквивалентное сопротивление схемы:
Ток источника ЭДС E2 равен:
Используя формулу разброса найдём токи:
По первому закону Кирхгофа найдём ток I6²:
Составим уравнение для контура ACDA по второму закону Кирхгофа:
Выразим ток I5²:
Оставшиеся токи найдём по закону Кирхгофа:
Вычисляем действительные токи ветвей исходной цепи (рисунок 1), выполняя алгебраическое сложение частных токов от каждой ЭДС, учитывая их направление:
Источники E1 и E2 вырабатывают электрическую энергию, т.к. направление ЭДС и тока в ветвях с источниками совпадают. Баланс мощностей для заданной цепи запишется так:
Подставляем числовые значения и вычисляем баланс мощностей.
22,960 Вт = 22,973 Вт.
С учетом погрешности расчетов баланс мощностей получился.
1.1.5 Результаты расчетов токов по пунктам 1, 2 и 3 представить в виде таблицы и сравнить.
Таблица 1.
Расчет токов ветвей тремя методами с учетом ошибок вычислений практически одинаков.
1.1.6 Метод эквивалентного генератора. Метод эквивалентного генератора используется для исследования работы
Для решения задачи методом эквивалентного генератора разделим электрическую цепь на две части: потребитель (исследуемая ветвь с сопротивлением R2, в которой требуется определить величину тока I2) эквивалентный генератор (оставшаяся часть цепи, которая для потребителя R2 служит источником электрической энергии, т.е. генератором). Получается схема замещения (рисунок 7) На схеме искомый ток I2, определяем по закону Ома для замкнутой цепи:
где ЕЭ=UХХ – ЭДС эквивалентного генератора, ее величина определяется как напряжение на зажимах генератора в режиме холостого хода. RЭКВ – внутреннее сопротивление эквивалентного генератора, величина которого рассчитывается как эквивалентное сопротивление пассивного двухполюсника относительно исследуемых зажимов.
Для того чтобы найти напряжение холостого хода необходимо найти токи, действующие в контуре ABCA. Для этого «сворачиваем» схему (рисунок 9).
Эквивалентное сопротивление цепи:
Ток создаваемый источником ЭДС Е1 по закону Ома:
Напряжение холостого хода равно:
Чтобы найти напряжение холостого хода нам необходимо найти токи I3 и I4. Из схемы видно, что: I1 = I3 = 0,181 A. По формуле разброса, ток I4 равен:
Найдём напряжение холостого хода.
Эквивалентное сопротивление цепи, изображённой на рисунке 10 можно взять из «метода наложения» при отсутствии источника ЭДС E1. Необходимо только выделить из него сопротивление потребителя R2 и добавить внутреннее сопротивление источника ЭДС Е2.
Зная ЭДС и внутреннее сопротивление эквивалентного генератора, вычисляем ток I2:
1.1.7 Построить потенциальную диаграмму для контура ABDCA (рисунок 1)
Зададимся обходом контура по часовой стрелке. Заземлим одну из точек контура. Пусть это будет точка D. Потенциал этой точки равен нулю: jD=0 В (рисунок 11). Зная величину и направление токов ветвей и ЭДС, а также величины сопротивлений, вычислим потенциалы точек при переходе от элемента к элементу. Начнем обход с точки F: Потенциал точки F:
Потенциал точки A:
Потенциал точки G:
Потенциал точки C:
Потенциал точки B:
Строим потенциальную диаграмму. По оси абсцисс откладываем сопротивление контура в той последовательности, в которой производим обход контура, прикладывая сопротивления, друг к другу, по оси ординат – потенциалы точек с учетом их знаков.
1.2 Расчет нелинейных электрических цепей постоянного тока. Построить входную вольтамперную характеристику схемы (рисунок 12).
Дано: U=120 B, R3=24 Ом Определить: I1, I2, I3, U1, U2, U3.
Расчет цепи производим графическим методом. Для этого в общей системе координат строим вольтамперные характеристики (ВАХ) линейного и нелинейных элементов: I1=f(U1), I2=f(U2), I2=f(U3) (рисунок 13).
Далее строим общую ВАХ цепи с учетом схемы соединения элементов. В нашей цепи (рисунок 12) соединение элементов смешанное. Поэтому графически “сворачиваем” цепь. Начнем с разветвлённого участка. Нелинейные элементы соединены параллельно, их ВАХ I1=f(U1) и I2=f(U2). С учётом этого строим общую для них ВАХ. Для этого задаемся напряжением и складываем токи при этом напряжении I12=U1+U2. Точка пересечения этих значений (тока и напряжения) дает одну из точек их общей ВАХ. В результате получаем множество точек и по ним строим ВАХ I12=f(U12) изображенную на рисунке 13. Далее мы имеем характеристики нелинейного элемента I3=f(U3) и нелинейных элементов I12=f(U12), которые соединены между собой последовательно. Строим для них общую ВАХ. В данном случае задаемся током и складываем напряжения U=U12+U3. Проделаем это многократно. По полученным данным строим общую ВАХ цепи I=f(U) (рисунок 13). Дальнейший расчет цепи производим по полученным графикам. Чтобы найти токи и напряжения на всех элементах цепи поступаем следующим образом: по оси напряжений находим значение напряжения, равное 120 В (точка «а»). Из этой точки восстанавливаем перпендикуляр до пересечения с общей ВАХ цепи I=f(U), получим точку «в». Из точки «в» пускаем перпендикуляр до пересечения с осью токов (точка «с»). Отрезок «ос» дает нам искомое значение общего тока I3=3,25 А. Когда мы опускали перпендикуляр из точки “в” к точке «с», то пересекли ВАХ I3=f(U3) и I12=f(U12) в точках «e» и «f» соответственно. Опуская перпендикуляры из этих точек на ось напряжений, получим значения напряжений на этих участках цепи:
U12=41,5 А. Когда мы опускали перпендикуляр к оси напряжений из точки «f», то пересекли ВАХ I1=f(U1) и I2=f(U2) в точках «n» и «m». Проведя из этих точек перпендикуляр на ось токов, получаем токи на участках цепи I1=0,9 A, и I2=2,3 A. В результате имеем следующие значения токов и напряжений на всех элементах цепи:
2 АНАЛИЗ ЭЛЕКТРИЧЕСКОГО СОСТОЯНИЯ ЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ПЕРЕМЕННОГО ТОКА: ОДНОФАЗНЫХ, ТРЕХФАЗНЫХ.
2.1 Расчет однофазных линейных электрических цепей переменного тока. К зажимам электрической цепи, схема замещения которых приведена на (рисунок 14) подключен источник синусоидального напряжения Параметры элементов схемы замещения: R1=50 Ом, R2=100 Ом, L1= Выполнить следующее: 1) определить реактивные сопротивления элементов цепи; 2) определить действующие значения токов во всех ветвях цепи; 3) записать уравнение мгновенного тока источника; 4) составить баланс активных и реактивных мощностей; 5) построить векторную диаграмму токов, совмещенную с топографической векторной диаграммой напряжений.
Дано: UМ=540 B, yu=-45° град, R1=50 Ом, R2=100 Ом, L1=
Т.к. XC2=XL2, то в нашей цепи резонанс токов. Поэтому необходимо исключить ветвь с резонансом из нашей схемы для дальнейшего расчёта (рисунок 15).
2.1.2 Расчет токов в ветвях цепи выполняем методом эквивалентных преобразований. Нарисуем схему замещения элементов для цепи, приведенной на рисунке 15:
Находим комплексные сопротивления ветвей, затем участков цепи и всей цепи:
Выразим действующие значение напряжение в комплексной форме:
Вычисляем токи ветвей и общий ток цепи:
2.1.3 Уравнение мгновенного значения тока источника:
2.1.4 Комплексная мощность цепи:
где
Активная Pпр и реактивная Qпр мощности приемников.
Баланс мощностей выполняется: Pист=Pпр; Qист=Qпр; или в комплексной форме:
2.1.5 Напряжения на элементах:
2.1.6 Строим топографическую диаграмму на комплексной плоскости. Выбираем масштаб: МI=0,84 A/см, МU=34 B/см. Определяем длины векторов токов и напряжений:
На комплексной плоскости в масштабе откладываем векторы токов в соответствии с расчетными значениями, при этом положительные фазовые углы отсчитываем от оси (+1) против часовой стрелки, а отрицательные – по часовой стрелке. Так вектор тока Топографическая векторная диаграмма напряжений характерна тем, что каждой точке диаграммы соответствует определенная точка электрической цепи и ориентируя векторы напряжений относительно векторов тока. На активном сопротивлении ток и напряжение совпадают по фазе, на индуктивном элементе напряжение опережает ток на 90°, а на емкостном напряжение отстает от тока на 90°. Направление обхода участков цепи выбираем, как принято, противоположно положительному направлению токов. Обход начинаем с точки «a», потенциал которой примем за исходный (ja=0). Точку «a» помещаем в начало координат комплексной плоскости. При переходе от точки «a» к точке «b» потенциал повышается на величину падения напряжения на активном сопротивлении R1. Вектор этого напряжения Uab совпадает с вектором тока I1. Конец вектора Uab определяет потенциал точки «b». При переходе от точки «b» к точке «c» потенциал повышается на величину падения напряжения на индуктивном сопротивлении XL1. Вектор этого напряжения Ubc опережает вектор тока I1 на 90°. Конец вектора Ubc определяет потенциал точки «c». Аналогично строим векторы напряжения других участков цепи, сохраняя обход на встречу току.
2.2 Расчет трехфазных электрических цепей переменного тока.
Известно фазное напряжение UЛ=1038 В и сопротивление фаз: RA=115 Ом; RB=63 Ом; RС=78 Ом; XLA=164 Ом; XLC=290 Ом; XCB=135 Ом. Определить полное сопротивление фаз, фазные и линейные токи, активную, реактивную, полную мощности каждой фазы и всей цепи.
Дано: UЛ=1038 В; RA=115 Ом; RB=63 Ом; RС=78 Ом; XLA=164 Ом; XLC=290 Ом; XCB=135 Ом.
Определить: ZA, ZB, ZC, IA, IB, IC, IN, P, Q, S.
ГРАФОАНАЛИТИЧЕСКИЙ МЕТОД РАСЧЁТА (расчёт с применением диаграмм) При соединении звездой
Так как есть нейтральный провод, то UФ=UA=UB=UC=600 B. Вычисляем сопротивление фаз и углы j определяем по диаграммам сопротивлений.
Фазные токи можно определить следующим образом:
Чтобы вычислить ток в нейтральном проводе, нужно построить векторную диаграмму цепи. На векторной диаграмме под углом 120° друг относительно друга строятся векторы фазных напряжений одинаковой длины. Векторы фазных токов строятся в масштабе под вычисленными углами j по отношению к фазным напряжениям. В фазе А нагрузка носит индуктивный характер, значит ток IА отстаёт от напряжения UA на угол jА. В фазе В нагрузка носит ёмкостной характер, значит ток IВ опережает напряжение UB на угол jВ.
Масштаб:
Ток в нейтральном проводе равен геометрической (векторной) сумме фазных токов:
Измерив длину вектора,
Активная мощность трёхфазной цепи:
Определим реактивные мощности фаз:
Реактивная мощность трёхфазной цепи:
Полная мощность каждой фазы:
Полная мощность трёхфазной цепи:
СИМВОЛИЧЕСКИЙ МЕТОД. Строгий аналитический расчёт трёхфазных цепей производится символическим методом, т.е. в комплексной форме.
Выразим в комплексной форме фазные напряжения:
Выразим сопротивления фаз в комплексной форме:
где
где
где
Определяем фазные токи:
модуль IA = 2,995 А; yA = -54,961°;
модуль IB = 1,027 А; yB = -55,015°;
модуль IC = 1,998 А; yС = 45,054°.
Вычисляем ток в нейтральном проводе:
модуль IN = 6,957 А; yС = -38,563°.
Вычисляем мощность каждой фазы всей цепи:
где SA=1797
где SВ=2416,2

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 лист
лист Введение.
Введение.
 1 АНАЛИЗ ЭЛЕКТРИЧЕСКОГО СОСТОЯНИЯ ЛИНЕЙНЫХ И НЕЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ПОСТОЯННОГО ТОКА
1 АНАЛИЗ ЭЛЕКТРИЧЕСКОГО СОСТОЯНИЯ ЛИНЕЙНЫХ И НЕЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ПОСТОЯННОГО ТОКА Метод узловых и контурных уравнений основан на применении первого и второго законов Кирхгофа. Он не требует никаких преобразований схемы и пригоден для расчёта любой цепи.
Метод узловых и контурных уравнений основан на применении первого и второго законов Кирхгофа. Он не требует никаких преобразований схемы и пригоден для расчёта любой цепи. . Составляем три уравнения для любых трёх узлов, например для узлов A, B и D:
. Составляем три уравнения для любых трёх узлов, например для узлов A, B и D:





 Падение напряжения на сопротивлении контура берётся со знаком «+», если направление тока в нём совпадает с обходом контура, со знаком «–», если не
Падение напряжения на сопротивлении контура берётся со знаком «+», если направление тока в нём совпадает с обходом контура, со знаком «–», если не







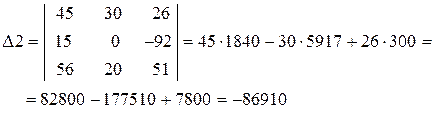
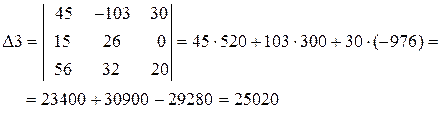






 Если при решении системы ток получается со знаком «–», значит его действительное направление обратно тому направлению, котором мы задались.
Если при решении системы ток получается со знаком «–», значит его действительное направление обратно тому направлению, котором мы задались. . Где n - количество узлов в схеме
. Где n - количество узлов в схеме На основании выше изложенного, порядок расчета цепи методом контурных токов будет следующим:
На основании выше изложенного, порядок расчета цепи методом контурных токов будет следующим:
















 По методу наложения ток в любом участке цепи рассматривается как алгебраическая сумма частных токов, созданных каждой ЭДС в отдельности.
По методу наложения ток в любом участке цепи рассматривается как алгебраическая сумма частных токов, созданных каждой ЭДС в отдельности.















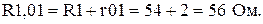
 Чтобы «свернуть» схему нам необходимо преобразовать треугольник с сопротивлениями R1,01; R3; R5 в эквивалентную звезду с сопротивлениями RD, RE, RF (рисунок 6).
Чтобы «свернуть» схему нам необходимо преобразовать треугольник с сопротивлениями R1,01; R3; R5 в эквивалентную звезду с сопротивлениями RD, RE, RF (рисунок 6).











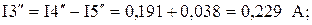







 1.1.4 Составить баланс мощностей для заданной схемы (рисунок 1).
1.1.4 Составить баланс мощностей для заданной схемы (рисунок 1).


 какого-либо участка в сложной электрической цепи.
какого-либо участка в сложной электрической цепи.
 Изображаем схему эквивалентного генератора в режиме холостого хода, т.е. при отключённом потребителе R2 от зажимов а и б (рисунок 8). Обозначим токи в контурах напряжение холостого хода.
Изображаем схему эквивалентного генератора в режиме холостого хода, т.е. при отключённом потребителе R2 от зажимов а и б (рисунок 8). Обозначим токи в контурах напряжение холостого хода.

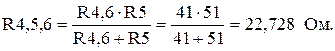












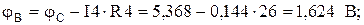
 Потенциал точки D:
Потенциал точки D: - проверочная точка.
- проверочная точка. Определить токи во всех ветвях схемы и напряжение на отдельных элементах, используя полученные вольтамперные характеристики элементов “б” и “а”.
Определить токи во всех ветвях схемы и напряжение на отдельных элементах, используя полученные вольтамперные характеристики элементов “б” и “а”. ВАХ линейного элемента строим по закону Ома для участка цепи
ВАХ линейного элемента строим по закону Ома для участка цепи  . Она представляет собой прямую, проходящую через начало координат. Для определения второй точки ВАХ линейного элемента задаемся произвольным значением напряжения. Например, напряжение на линейном элементе возьмем равным 36 В (UR=36 B), тогда соответствующее значение тока определяется по формуле
. Она представляет собой прямую, проходящую через начало координат. Для определения второй точки ВАХ линейного элемента задаемся произвольным значением напряжения. Например, напряжение на линейном элементе возьмем равным 36 В (UR=36 B), тогда соответствующее значение тока определяется по формуле  . Мы получили координаты второй точки ВАХ линейного элемента (36; 1,5). Соединив полученную точку с началом координат, получим ВАХ линейного элемента (рисунке 13) I3=f(U3).
. Мы получили координаты второй точки ВАХ линейного элемента (36; 1,5). Соединив полученную точку с началом координат, получим ВАХ линейного элемента (рисунке 13) I3=f(U3). U3=78,5 А
U3=78,5 А
 B, частотой 50 Гц.
B, частотой 50 Гц. Гн, L2=
Гн, L2=  Гн, С1=
Гн, С1=  Ф, С2=
Ф, С2=  Ф.
Ф. 2.1.1 Реактивное сопротивление элементов цепи:
2.1.1 Реактивное сопротивление элементов цепи:







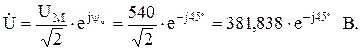























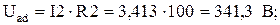
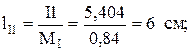






 1 повернут относительно действительной оси (+1) на угол -89,958°, то есть по часовой стрелке и его длина 6 см, вектор тока
1 повернут относительно действительной оси (+1) на угол -89,958°, то есть по часовой стрелке и его длина 6 см, вектор тока 
 В цепи изображенной на схеме (рисунок 16) потребители трехфазного тока соединены звездой.
В цепи изображенной на схеме (рисунок 16) потребители трехфазного тока соединены звездой. , поэтому:
, поэтому:



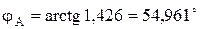 - в фазе А напряжение опережает ток на 54,961°.
- в фазе А напряжение опережает ток на 54,961°.

 - в фазе В напряжение отстаёт от тока на 53,123°.
- в фазе В напряжение отстаёт от тока на 53,123°.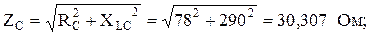

 - в фазе С напряжение опережает ток на 74,946°.
- в фазе С напряжение опережает ток на 74,946°.


 В фазе C нагрузка носит индуктивный характер, значит ток IC отстаёт от напряжения UC на угол jА.
В фазе C нагрузка носит индуктивный характер, значит ток IC отстаёт от напряжения UC на угол jА.




 , находим ток
, находим ток 

 Определим активные мощности фаз:
Определим активные мощности фаз: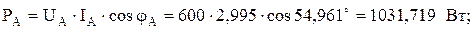

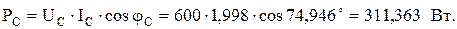














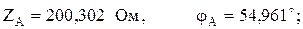










 , PA=1031,719 Вт, QA=1471,314 вар.
, PA=1031,719 Вт, QA=1471,314 вар.
