|
|
Тема 2. Решение уравнения Шредингера для простейших систем.Перейдем к описанию методов решения уравнения Шредингера для простейших систем: частицы в потенциальном ящике, гармонического осциллятора, ротатора. Рассмотрение их представляет интерес не только для квантовой механики, но и имеет большое значение для изучения молекулярных и кристаллических систем методами молекулярной спектроскопии и квантовой статистики.
2.1. Частица в потенциальном ящике. В качестве модели потенциального ящика с бесконечными по высоте стенками рассмотрим движение частицы, на потенциальную энергию которой наложены условия:
Для одномерного движения уравнение Шредингера имеет следующий вид:
Поскольку согласно постулатам квантовой механики уравнение Шредингера должно быть справедливо во всей области изменения переменных (в нашем случае - ¥ < x < + ¥), то для потенциальной энергии, заданной уравнением 2.1, в точках x = 0 и x = a волновая функция должна обращаться в нуль, т.е.
Но, с другой стороны, при
Т.о., с математической точки зрения решение задачи сводится к решению уравнения 2.4 с граничными условиями 2.3. Общим решением уравнения 2.4 будет
Приняв во внимание граничное условие
или
т.е.
Учет граничных условий привел к выводу, что наблюдаются не все значения энергии, а лишь некоторые, т.е. можно говорить о квантовании энергии системы. Приняв во внимание выражение (2.8) для энергии, можно записать цепочку равенств, позволяющих конкретизировать вид волновой функции:
Постоянную С1 определим из условия нормировки:
Отсюда,
Таким образом,
Здесь n - квантовое число. Обсудим полученные решения. 1. Энергия частицы в потенциальном ящике приобретает не любые, но строго определенные квантовые значения, причем при увеличении квантового числа n энергия возрастает. Разность энергий различных энергетических уровней изменяется как разность квадратов двух целых чисел. 2. Попробуем изобразить волновые функции yn (x) для различных n (рис. 2.1).
Рис.2.1. Волновые функции yn(х) для прямоугольного потенциального ящика.
Из рис.2.1 видно, что "нулевая энергия", Е1, соответствует состоянию, в котором частица с наибольшей вероятностью находится в центре ящика, т.е. как можно дальше от стенок. Однако с точки зрения классической механики вероятность нахождения частицы в любой точке ящика за исключением х = 0 и х = а одинакова. Кроме того, волновые функции yn(х), при n ³ 2 имеют узлы, т.е. значения х, при которых yn(х) = 0. Различие в вероятностях нахождения частицы в различных точках при 0 < x < a является чисто квантовым явлением. 3. При уменьшении размера ящика, а, расстояния между энергетическими уровнями увеличиваются, поскольку целое число полуволн должно расположиться в меньшей по размеру области пространства. При увеличении размера ящика расстояния между энергетическими уровнями уменьшаются. В предельном случае бесконечно широкого ящика энергии образуют непрерывную последовательность, т.е. сливаются. При этом система перестает описываться уравнениями квантовой механики. Иначе говоря, она переходит в классический предел, и ее поведение описывается законами классической механики. 4. Увеличение массы частицы приводит к такому же эффекту, что и увеличение размеров ящика. Поведение частицы, имеющей большую массу, в ящике заданного размера в большей степени определяется законами классической механики, чем поведение частицы малой массы. Модель частицы в потенциальном ящике используется при описании p-электронных систем в сопряженных полиенах. Атомный скелет сопряженной системы рассматривают как одномерный потенциальный ящик с постоянной потенциальной энергией внутри (системы сопряженных связей) и бесконечно большой – вне ящика. Обычно предполагается, что длина ящика равна длине сопряженной полиеновой цепи, увеличенной на одно звено с каждого конца. Такое искусственное удлинение цепи необходимо для того, чтобы области пространства, где волновая функция yn(х) принимает нулевые значения, не попадали на концевые атомы цепи. Решения такой задачи рассматриваются как волновые функции, на каждой из которых находятся два электрона. Их заполнение электронами осуществляется в порядке возрастания энергии до тех пор, пока не разместятся все p-электроны. Полученные результаты легко обобщаются на трехмерный случай:
Здесь a, b, c – размеры ящика в направлениях x, y, z. 2.2. Линейный гармонический осциллятор Колебательная система, представляющая собой частицу с массой m, совершающую движение по прямой линии под действием силы, F, пропорциональной смещению частицы, х, от положения равновесия, называется линейным гармоническим осциллятором. Запишем уравнение Шредингера для одномерного движения частицы
а потенциальную энергию гармонического осциллятора - в виде
где w - частота собственных колебаний осциллятора, а х – смещение колеблющейся системы от положения равновесия. Пусть
С учетом выражений 2.15-2.17 уравнение Шредингера приобретает вид
Легко заметить, что при
Пусть
где
Решение этого уравнения будет либо полиномом от х, либо пропорционально exp(l×x2). Разложим
Подставляя выражение 2.21 в уравнение 2.20 и приравнивая нулю суммы членов при одинаковых степенях х, получаем следующее рекуррентное соотношение:
При j ® ¥ имеет место равенство
Такое рекуррентное соотношение справедливо для степенного разложения функции exp(l×x2). Но функция exp(l×x2) при x ® ± ¥ становится неограниченно большой. Чтобы решение в виде 2.19 было ограниченным, необходимо предположить
Тогда
т.е.
Отсюда
при n = 0, 1, 2, …. Здесь n – колебательное квантовое число. Можно показать, что волновая функция в этом случае имеет вид
Для иллюстрации выпишем несколько волновых функций
В формуле 2.23 Hn(x) – полином Чебышева-Эрмита. Обсудим полученные решения: 1. Энергия гармонического осциллятора квантована и принимает ненулевое значение Расстояние между соседними энергетическими уровнями равно 2. На рис.2.2 приведено графическое изображение функций yn(x) для гармонического осциллятора с различными n:
Рис.2.2. Волновые функции гармонического осциллятора.
Из рис.2.2. видно, что волновая функция при n ³ 1 имеет узлы, причем количество их равно n. Кроме того, при увеличении энергии уровня, главные максимумы квадрата волновой функции (т.е. вероятность нахождения частицы) оказываются преимущественно на краях распределения, где при классическом рассмотрении находятся точки поворота. Важность гармонического осциллятора как модели определяется тем, что наблюдаемые в природе колебания достаточно часто являются гармоническими. Чаще всего эту модель с успехом используют при описании колебаний атомов и молекул в твердых телах. Поэтому гармонический осциллятор используется при рассмотрении теплоемкости и многих других свойств твердых тел.
2.3. Движение в центральном поле. Квантово-механическая модель атома водорода. Водородоподобные атомы можно представить как системы, состоящие из двух частиц, ядра массой М, имеющего положительный заряд Z× e0, и электрона с массой m0 и отрицательным зарядом e0, движущегося в поле ядра. Предположим, что движется только электрон. Учет движения ядра приведет к тому, что в уравнении Шредингера массу электрона необходимо будет заменить на приведенную массу системы:
Водородоподобный атом описывается при помощи уравнения Шредингера
где r - расстояние от электрона до ядра.
Поскольку функция потенциальной энергии имеет сферическую симметрию, то эту задачу легче решить, если перейти от прямоугольных координат к сферическим. В сферических координатах
где
и в уравнении Шредингера возможно разделение переменных. Для этого волновую функцию представим в виде произведения радиальной и угловой частей:
Легко показать, что константа разделения переменных равна
где Уравнение 2.30 является разновидностью уравнения Лежандра. Его решения - так называемые сферические гармоники.
После простых алгебраических преобразований легко получается уравнение для радиальных частей
Решением уравнения 2.32 являются следующие собственные значения
Уравнение 2.32 с собственными значениями 2.33 имеет в качестве собственных функций Rnl(r), общий вид которых
где Условие нормировки для радиальных функций имеет вид:
В общем случае сферические гармоники 2.31 являются комплексными функциями (при m ¹ 0). Для их наглядного изображения можно использовать следующие их действительные и ортогональные линейные комбинации. Используя формулы Эйлера, имеем
Для иллюстрации приведем явные выражения для собственных функций водородоподобных атомов. (Здесь
Приведенные формулы слишком сложны для использования в повседневной практике химика. Однако они несут весьма ценную информацию об особенностях пространственного распределения электронов. Поэтому химики чаще всего используют графические изображения волновых функций или их линейных комбинаций. Обычно строят распределение вероятности положения электрона на шаровой поверхности 2.4. Свойства атомных орбиталей. Приведенные выше атомные орбитали (АО) обладают тем свойством, что их вид и энергия зависят от набора некоторых чисел, называемых квантовыми. Остановимся на физическом свойстве этих чисел. Постоянная n называется главным квантовым числом. Оно определяет энергию электрона и "быстроту" уменьшения волновой функции при увеличении расстояния от ядра. Кроме n в выражение для волновой функции входит число В выражение для волновых функций входит также число При отсутствии возмущающего поля уровни энергии с одинаковыми n, но различными Значения орбитального квантового числа принято обозначать латинскими буквами, причем имеет место соответствие:
На рис.2.3 приведено схематическое изображение атомных орбиталей водородоподобного атома.
Рис. 2.3. Схематическое изображение атомных орбиталей водородоподобного атома.
Рассмотрим свойства каждой из АО более подробно. Прежде всего следует отметить следующие общие свойства АО. 1. Размеры АО увеличиваются с ростом n. 2. Любая АО обращается в нуль (т.е. имеет узлы) 3. Среди АО с одним и тем же n наибольшую электронную плотность вблизи ядра имеют те, у которых 4. S- и d-АО симметричны, а p- и f-АО антисимметричны относительно отражения в центре инверсии, i. S-Атомные орбитали. ns-АО обладают следующими свойствами. 1. Сферической симметрией относительно ядра. 2. В районе расположения ядра имеют ненулевое значение. 3. Количество узлов ns-АО равно n-1, где n - главное квантовое число. Узловые поверхности-сферы для ns-АО расположены на расстояниях k × aВ, k = 1, … n-1. В то время, как ns-состояния не зависят от выбора направления в пространстве, и распределение электронной плотности, описываемое ими, сферически симметрично, состояния np, nd, nf зависят от углов q и j, и, следовательно, распределение электронной плотности по различным направлениям неодинаково.
p-Атомные орбитали. Если функцию ynp изобразить графически в виде зависимости от углов q и j, то вместо сферической симметрии ns-АО в пространстве возникает преимущественное направление с наибольшим значением функции, направление оси z для pz, оси y – для py, оси x – для px. Важно отметить, что для этих функций существуют узловые плоскости, где функции меняют свой знак. Для рх-АО плоскость zoy, для рy – плоскость zox и для pz-АО – плоскость xoy. С увеличением np-АО становятся более вытянутыми в пространстве.
d-Атомные орбитали. Вид этих АО показан на рис.2.3. Отметим лишь некоторые их особенности. 1. 2. Все пять d-АО имеют различным образом расположенные узловые поверхности. Для
Для
Литература к главе 2. 1. П.Эткинс. Кванты. Справочник концепций.М.Мир.1977.С.101-105; 410-414; 75-86; 465-469. 2. З.Флюге Задачи по квантовой механике. Т.1.М.Мир.1974.С.81-84. 3. Л.А.Грибов, С.П.Муштакова Квантовая химия. М.Гардарики.1999. С.23-24. 4. Дж.Маррел, С.Кеттл, Дж.Теддер Теория вероятности. М.Мир. 1968.С.32-47. 5. С.Фудзинага Метод молекулярных орбиталей. М.Мир.1983.С.15-20. 6. Л.Цюлике Квантовая химия.Т.1. Основы и общие методы.М.Мир. 1976.С.81-112. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
при 
(2.1)
(2.2)
(2.3)
уравнение (2.2) приобретает вид:
(2.4)
(2.5)
, получим, что С2 = 0. С другой стороны, граничное условие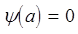 
означает, что
, (2.6)
, где n = 1,2,3,..., (2.7)
. (2.8)
(2.9)
. (2.10)
(2.11)
(2.12)
(2.13)
, (2.15)
, (2.16)
. (2.17)
(2.18)
имеет место отношение пропорциональности
, (2.19)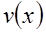
– удовлетворяет уравнению
(2.20)
(2.21)
.
,
.
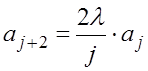
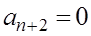(2.22)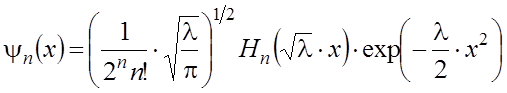
(2.23)
,
,
и т.д.
при n = 0. Таким образом, даже при абсолютном нуле энергия колебаний не равна нулю.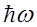
, т.е. они эквидистантны.
(2.24)
(2.25)
(2.26)
(2.27)
, (2.28)
(2.29)
, причем
(2.30)
.
(2.31)
(2.32)
(2.33)
(2.42)
- боровский радиус; n - целое число илинуль; 
- присоединенный полином Лагерра.
(2.35)
).
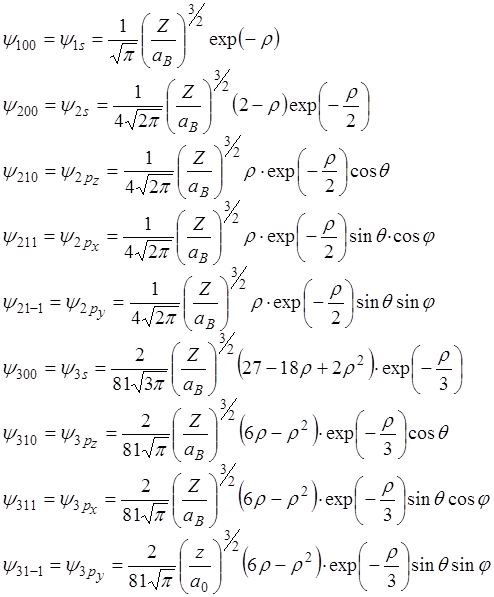
в зависимости от ее 
.
.Оно называется орбитальным или азимутальным квантовым числом и определяет значения момента количества движения, равного 
, а также форму (вид) волновой функции.
- магнитное квантовое число,определяющее величину проекции момента количества движения, равную 
, а также ориентацию волновой функции в пространстве.
и 
, совпадают.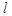
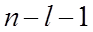раз для радиус-вектора r между 0 и ¥.
меньше, причем главный максимум тем дальше от ядра, чем меньше 
.
- АО концентрируется в направлении z, причем вдоль оси zона имеет большую концентрацию, чем pz-АО.
узловыми поверхностями являются координатные плоскости. Для 
-АО – взаимноперпендикулярные плоскости, расположенные по биссектрисам углов (45°) между координатными осями перпендикулярно к плоскости xOy.