
|
|
Достаточный признак сходимости знакопеременного ряда12 Теорема 2. Знакопеременный ряд
сходится, если сходится ряд, составленный из модулей его слагаемых
Определение 3. Знакопеременный ряд называется абсолютно сходящимся, если сходится сам этот ряд и ряд, составленный из модулей его слагаемых. Определение 4. Знакопеременный ряд называется условно сходящимся, если сам этот ряд сходится, а ряд, составленный из модулей его слагаемых, расходится. Пример 2. Исследовать сходимость ряда
Решение. Исследуем сходимость ряда, составленного из модулей членов исходного ряда
Данный ряд сходится, следовательно, согласно Теореме 2, исследуемый знакопеременный ряд абсолютно сходящийся.
Пример 3. Исследовать сходимость ряда
Решение. Ряд знакочередующийся. Исследуем его сходимость с помощью признака Лейбница. 1. Видим, что абсолютные величины слагаемых ряд монотонно убывают. 2. Условия признака Лейбница выполнены, ряд сходится. Чтобы определить абсолютную или условную сходимость данного ряда, исследуем на сходимость ряд, составленный из модулей его слагаемых.
Это гармонический ряд, который расходится. Следовательно, ряд
Исследовать ряды на абсолютную и условную сходимость:
62. 65. 68. 71. 74.
Функциональные ряды Пусть U1(x), U2(x),…, Un(x),… некоторая последовательность функций аргумента х. Определение 1. Выражение вида
называется функциональным рядом. Если рассмотреть ряд (5.5) в точке х = х0, то получим числовой ряд
Определение 2. Функциональный ряд (6.5) называется сходящимся в точке х = х0, если сходится числовой ряд (6.6). При этом точка х = х0 называется точкой сходимости ряда (6.5). Определение 3. Множество всех точек сходимости функционального ряда (6.5) называется его областью сходимости. Пример 1. Найти область сходимости функционального ряда
Решение. Исследуем сходимость ряда с помощью признака Даламбера, полагая Для любого х имеем:
Данный ряд сходится, если выполняется условие Каждому значению х из области сходимости ряда (6.5) соответствует определенное значение величины S(x) = U1(x) + U2(x) + U3(x) + … + Un(x) + … Сумма ряда S(x) может быть представлена в виде S(x) = Sn(x) + rn(x), где Sn(x) = U1(x) + U2(x) + … + Un(x) – частичная сумма ряда; rn(x) = Un+1(x) + Un+2(x) + … - остаточный член.
Найти область сходимости функционального ряда
77. 79. 81. 83. Степенные ряды 1. Определение степенного ряда Определение 1. Степенным рядом называется функциональный ряд вида
где х – независимая переменная; х0 – фиксированное число; а0, а1, а2,…, аn,… - действительные числа, называемые коэффициентами ряда. В результате замены х – х0 = z степенной ряд (5.7) примет вид:
Следовательно, в дальнейшем можно ограничиться изучением степенных рядов вида 2. Область сходимости степенного ряда Рассмотрим степенной ряд
Для данного ряда существует конечное или бесконечное число R, называемое радиусом сходимости, такое, что если: 1) | х | < R, то ряд сходится на интервале (-R; R), который называется интервалом сходимости степенного ряда; 2) | х | > R, то ряд расходится; 3) | х | = R, т. е. х = ±R, то может иметь место и сходимость, и расходимость в каждой из этих точек, причем, при R = ¥ областью сходимости является интервал (- ¥; +¥); при R=0 ряд сходится в одной единственной точке х=0. Замечание. На концах интервала сходимости (-R; R) степенного ряда (6.8) может иметь место как сходимость, так и расходимость. При этом его областью сходимости будет является один из промежутков (-R; R), (-R; R], [-R; R), [-R; R]. Вопрос о сходимости ряда в граничных точках интервала сходимости решается отдельно для каждого ряда. Используя признак Даламбера, можно показать, что, если существует предел
Пример 1. Найти область сходимости ряда Решение. Найдем радиус сходимости ряда, используя формулу (6.9). Здесь
следовательно, ряд сходится на интервале (-1; 1). Исследуем сходимость ряда на концах интервала сходимости. Пусть х = 1, тогда имеем числовой ряд Пусть х = -1. После подстановки этого значения х в общий член исследуемого ряда получим знакочередующийся ряд
Этот ряд сходится по признаку Лейбница. Таким образом, областью сходимости степенного ряда является промежуток [-1; 1), т. е. ряд сходится для всех значений х, удовлетворяющихся двойному неравенству -1 £ х < 1. Пример 2. Найти область сходимости ряда Решение. Осуществляя замену х + 1 = z исходный ряд приводится к ряду вида
Таким образом, ряд Исследуем сходимость ряда на концах интервала сходимости. Пусть х = 0. Подставляя это значение х в исследуемый степенной ряд, получим ряд числовой Пусть х = -2. Подставляя в общий член ряда данное значение х, получим знакочередующийся ряд 1. 1 > Наблюдается убывание абсолютных величин слагаемых ряда с возрастанием номера n. 2. Оба условия теоремы Лейбница выполнены, следовательно, данный знакочередующийся ряд сходится. Из проведенного исследования сходимости степенного ряда на концах интервала сходимости, следует, что обе граничные точки х = 0 и х = -2 принадлежат области сходимости ряда, которая в данном случае совпадает с отрезком [-2; 0]. 3. Свойства степенных рядов Пусть степенной ряд сходится к функции S(x) в области ее определения, т. е.
тогда: 1. Сумма S(x) ряда (6.10) есть функция непрерывная в области его сходимости. 2. Если степенной ряд (6.10) сходится к функции S(x) для х Î [a; b], то его можно почленно интегрировать по любому промежутку из его области сходимости, причем ряд, полученный после интегрирования степенного ряда, имеет тот же интервал сходимости, а его сумма равна интегралу от суммы S(x) исходного ряда. Таким образом, если S(x) = 3. Ряд (5.10) можно почленно дифференцировать в каждой точке его области сходимости. При этом полученный ряд имеет тот же интервал сходимости, а его сумма равна производной от суммы S(x) первоначального ряда, т. е.
Замечание. Операции почленного дифференцирования и интегрирования можно производить сколько угодно раз. Пример 3. Исследовать сходимость ряда
и найти его сумму. Решение. Данный ряд составлен из членов бесконечной геометрической прогрессии со знаменателем q = x. Как известно, он сходится, когда | q | < 1, т. е. когда | х | < 1. Следовательно, областью сходимости данного ряда является интервал (-1; 1). Найдем сумму ряда по формуле
Тогда Пример 4. Найти сумму ряда
Решение. Рассмотрим ряд
При | х | < 1 его сумма Действительно, (1 + х + х2+ х3+ … + хn+ …)'= 1 + 2х + 3х2+ … + n xn-1 +… Тогда, согласно свойству 3 степенных рядов, сумма первоначального ряда равна производной от суммы ряда (5.11), т. е.
и, следовательно,
Пример 5. Найти сумму ряда
Решение. Дифференцируя почленно данный ряд, получим 1 + х + х2+ х3+ … + хn+ … = Суммой этого ряда при | х | < 1 является функция
Сумму первоначального ряда найдем, согласно свойству 2 степенных рядов, почленно проинтегрировав это выражение в пределах от 0 до х, т. е.
Найти область сходимости рядов
85. 88. 91. 94.
Ряд Тейлора Всякая функция, бесконечно дифференцируемая в некоторой окрестности точки х = х0 , может быть разложена в этой окрестности в сходящийся к данной функции степенной ряд.
если выполняется условие Коэффициенты ряда при этом представляются в виде
и называются коэффициентами Тейлора.
* n! = 1× 2 × 3 × … ×(n-1) × n («ЭН» факториал); 0! = 1; 1! =1. 
12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
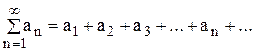
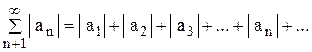

 .
.

 .
.
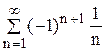 сходится условно.
сходится условно. ; 63.
; 63.  ; 64.
; 64. 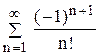 ;
; ; 66.
; 66. 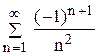 ; 67.
; 67.  ;
; ; 69.
; 69.  ; 70.
; 70.  ;
; ; 72.
; 72.  ; 73.
; 73. 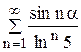 ;
; ; 75.
; 75.  ; 76.
; 76.  .
. (6.5)
(6.5) (6.6)
(6.6) .
. ,
,  .
.
 .
. , т. е.
, т. е.  . Следовательно, область сходимости ряда
. Следовательно, область сходимости ряда  ,
,  .
. , которую называют суммой функционального ряда. Причем область определения функции S(x) совпадает с областью сходимости данного ряда. Тогда говорят, что функция S(x) раскладывается в ряд:
, которую называют суммой функционального ряда. Причем область определения функции S(x) совпадает с областью сходимости данного ряда. Тогда говорят, что функция S(x) раскладывается в ряд: , поэтому для приближенных вычислений можно положить S(x) » Sn(x), | rn(x) | в этом случае представляет собой абсолютную погрешность приближения.
, поэтому для приближенных вычислений можно положить S(x) » Sn(x), | rn(x) | в этом случае представляет собой абсолютную погрешность приближения. ; 78.
; 78.  ;
;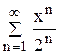 ; 80.
; 80.  ;
; ; 82.
; 82.  ;
;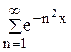 ; 84.
; 84.  .
. (6.7)
(6.7)
 .
. . (6.8)
. (6.8) , то радиус сходимости ряда (6.8) вычисляется по формуле
, то радиус сходимости ряда (6.8) вычисляется по формуле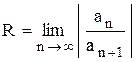 . (6.9)
. (6.9) .
. , тогда
, тогда ,
,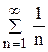 . Это гармонический ряд, который расходится.
. Это гармонический ряд, который расходится.
 .
. . Поступая аналогично тому, как это было сделано в предыдущем примере, получим
. Поступая аналогично тому, как это было сделано в предыдущем примере, получим .
.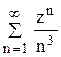 сходится при –1 < z < 1. Переходя к переменной х, получим –1 < x + 1 < 1 или –2 < x < 0, т. е. интервалом сходимости исходного ряда будет (-2; 0).
сходится при –1 < z < 1. Переходя к переменной х, получим –1 < x + 1 < 1 или –2 < x < 0, т. е. интервалом сходимости исходного ряда будет (-2; 0). - это сходящийся обобщенный гармонический ряд.
- это сходящийся обобщенный гармонический ряд. Для исследования его сходимости воспользуемся признаком Лейбница.
Для исследования его сходимости воспользуемся признаком Лейбница.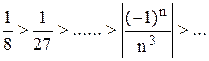
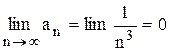 .
. , (6.10)
, (6.10) , то
, то  ; -R < x – x0 < R
; -R < x – x0 < R .
.
 , где а = 1, q = x.
, где а = 1, q = x. . Таким образом имеет место разложение
. Таким образом имеет место разложение 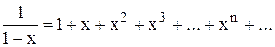
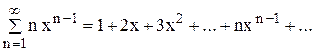 ( | x | < 1).
( | x | < 1).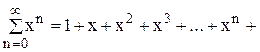 … (6.11)
… (6.11)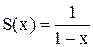 . Исходный ряд может быть получен при почленном дифференцировании данного ряда.
. Исходный ряд может быть получен при почленном дифференцировании данного ряда.
 .
. ( | х | < 1).
( | х | < 1).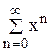 .
. (см. Пример 4).
(см. Пример 4).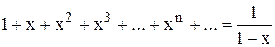 .
. ,
, .
. ; 86.
; 86.  ; 87.
; 87.  ;
; ; 89.
; 89.  ; 90.
; 90.  ;
; ; 92.
; 92.  ; 93.
; 93.  ;
; ; 95.
; 95.  ; 96.
; 96.  .
. (6.12)
(6.12)