
|
|
Интегральный признак Коши12 Глава VI. РЯДЫ Числовые ряды 1. Основные понятия Пусть дана бесконечная числовая последовательность а1, а2, а3,…, аn,…, где аn = f(n), n Î N. Выражение вида а1 + а2 + а3 + … + аn + … = называют числовым рядом. Числа а1, а2, а3,..., аn называют членами ряда, аn = f(n) - общим членом ряда. Будем полагать, что аi Î R, где i = 1, 2,…, n,… Определение 1. Суммы конечного числа членов ряда (6.1), начиная с первого, S1 = a1, S2 = a1 + a2 , S3 = a1 + a2 + a3,…, Sn = a1 + a2 + a3 + … + an называются его частичными суммами. Определение 2. Ряд (6.1) называется сходящимся, если его частичная сумма Sn при неограниченном возрастании n стремится к конечному пределу, т. е.
Число S называют суммой ряда. Если предел частичной суммы равен бесконечности или не существует, то ряд называется расходящимся. Нетрудно показать, что ряд а + аq + aq2 +…+ aqn + … = составленный из членов бесконечной убывающей геометрической прогрессии (знаменатель прогрессии |q| < 1 ), сходится, причем его сумма S = 2. Свойства сходящихся рядов 1. Если ряд 2. Если сходятся ряды Следствие 1. Сумма (разность) сходящегося и расходящегося рядов есть ряд расходящийся. Следствие 2. Сумма (разность) расходящихся рядов может быть и сходящимся и расходящимся рядом. 3. Если в ряде Записав ряд (6.1) в виде а1 + а2 + … + аn + an+1 + an+2 + … = обозначим сумму an+1 + an+2 + … = Следствие 3. Если ряд (6.1) сходится, то его остаток rn = an+1 + an+2 +… стремится к нулю при n ® ¥.
3. Необходимый признак сходимости ряда Теорема 1.Если ряд n ® ¥ равен нулю, т.е.
Следствие 4. Если предел общего члена ряда отличен от нуля или не существует при n ® ¥, то такой ряд расходится. Пример 1. Используя необходимый признак сходимости, исследовать сходимость ряда
Решение. Вычислим предел общего члена ряда аn =
По необходимому признаку сходимости данный ряд расходится. Условие Теоремы 1 является необходимым, но не достаточным условием сходимости ряда. Примером расходящегося ряда, удовлетворяющего необходимому признаку сходимости, является гармонический ряд 1+
Написать четыре-пять членов ряда по заданному общему члену аn и проверить выполняется ли необходимый признак сходимости
1. 4.
Написать формулу общего члена ряда и проверить выполняется ли необходимый признак сходимости
7. 8. 9. 10. 11. 12.
Проверить выполняется ли необходимый признак сходимости ряда
13. 15. 17.
4. Достаточные признаки сходимости рядов С положительными членами Первый признак сравнения
Пусть даны два ряда с неотрицательными членами
и для всех n выполняется условие an ³ bn. Тогда из сходимости ряда (6.2) следует сходимость ряда (6.3); а из расходимости ряда (6.3) - расходимость ряда (6.2). Замечание.Этот признак остается в силе, если неравенства an ³ bn выполняются, начиная с некоторого номера n = N. Пример 2. Исследовать сходимость ряда
Решение. Проверим сначала, выполняется ли необходимый признак сходимости ряда
Необходимый признак выполняется и, следовательно, ряд может как сходиться, так и расходиться. Для дальнейшего исследования сходимости ряда воспользуемся достаточным признаком – первым признаком сравнения. Для сравнения выберем ряд
Второй признак сравнения
Если существует конечный, отличный от нуля предел отношения общих членов рядов Пример 3.Исследовать сходимость ряда Решение. Воспользуемся вторым признаком сравнения. Сравним данный ряд
Таким образом, согласно второму признаку сравнения, из расходимости гармонического ряда следует расходимость ряда Замечание. В качестве рядов для сравнения необходимо выбирать ряды, сходимость или расходимость которых известна.
Признак Даламбера Пусть дан ряд с положительными членами Тогда: 1) если r < 1, то ряд сходится; 2) если r > 1, то ряд расходится; 3) если r = 1, то признак не определяет поведение ряда, необходимо использовать другие достаточные признаки сходимости. Пример 4. Исследовать сходимость ряда Решение. Воспользуемся признаком Даламбера. Имеем
Следовательно, данный ряд сходится по признаку Даламбера.
Пусть дан ряд Тогда: 1) если r < 1, то ряд сходится; 2) если r > 1, то ряд расходится; 3) если r = 1, то признак не определяет поведения ряда, необходимо использовать другие признаки. Пример 5. Исследовать сходимость ряда Решение. Здесь удобно воспользоваться радикальным признаком Коши, так как
Следовательно, данный ряд сходится по радикальному признаку Коши.
Интегральный признак Коши
Пусть дан ряд Пример 6. Исследовать сходимость ряда Решение. Воспользуемся интегральным признаком Коши. Для этого положим
= Как следует из данного примера, данный обобщенный гармонический ряд сходится при a > 1 и расходится при a< 1 (a = 1 соответствует расходящемуся гармоническому ряду).
Исследовать на сходимость ряды при помощи признаков сравнения
19. 22. 25.
Исследовать на сходимость ряды при помощи признака Даламбера
28. 31. 34.
Исследовать на сходимость ряды при помощи радикального признака Коши
37. 39.
Исследовать на сходимость ряды при помощи интегрального признака Коши
41. 44.
Исследовать ряды на сходимость
47. 50. 53. 56. 59. Знакопеременные ряды Определение 1. Ряд называется знакопеременным, если среди его слагаемых есть и положительные, и отрицательные.
1. Знакочередующиеся ряды
Определение 2. Знакопеременный ряд называется знакочередующимся, если положительные и отрицательные его члены следуют друг за другом поочередно.
Признак Лейбница (достаточный признак сходимости знакочередующегося ряда)
Теорема 1. Знакочередующийся ряд
сходится, если абсолютные величины его членов монотонно убывают с ростом порядкового номера, и общий член его стремится к нулю при n, стремящемся к бесконечности, т. е. если выполняются условия: 1. а1 > а2 > а3 > … > аn > … ; 2. При этом суммаS ряда (6.4) удовлетворяет неравенству 0 £ S £ a1 . Пример 1. Исследовать сходимость ряда
Решение. Ряд знакочередующийся, поэтому применим признак Лейбница. 1. Вычислим модуль отношения (n+1)-го и n-го членов ряда.
следовательно, слагаемые ряда убывают по модулю с ростом n; действительно 2. Оба условия признака Лейбница выполнены, следовательно, данный ряд сходится.
2. Абсолютная и условная сходимость рядов 
12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 (6.1)
(6.1) .
. ,
, .
. сходится и суммой его является число S, то для произвольного числа k ряд
сходится и суммой его является число S, то для произвольного числа k ряд  также сходится, причем его сумма равна k S.
также сходится, причем его сумма равна k S. , имеющие соответственно суммы S и s, то сходятся и ряды
, имеющие соответственно суммы S и s, то сходятся и ряды  , причем сумма каждого равна соответственно S ± s.
, причем сумма каждого равна соответственно S ± s. добавить или отбросить конечное число членов, то получится ряд, сходящийся или расходящийся одновременно с данным. В случае сходимости полученного ряда его сумма отличается на сумму добавленных или отброшенных членов.
добавить или отбросить конечное число членов, то получится ряд, сходящийся или расходящийся одновременно с данным. В случае сходимости полученного ряда его сумма отличается на сумму добавленных или отброшенных членов. и будем называть ее в дальнейшем n-м остатком ряда или его остаточным членом. Очевидно, что в случае сходимости ряда (6.1), rn = S – Sn.
и будем называть ее в дальнейшем n-м остатком ряда или его остаточным членом. Очевидно, что в случае сходимости ряда (6.1), rn = S – Sn. .
. .
. при n ® ¥.
при n ® ¥. = е ¹ 0.
= е ¹ 0. .
. ; 2.
; 2.  ; 3.
; 3.  ;
; ; 5.
; 5.  ; 6.
; 6.  .
. ;
; ;
; ;
; …;
…; ;
; .
. ; 14.
; 14.  ;
; ; 16.
; 16.  ;
; ; 18.
; 18.  .
. , (6.2)
, (6.2) bn ³ 0.(6.3)
bn ³ 0.(6.3) .
.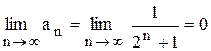 .
. , члены которого больше соответствующих членов исследуемого ряда, т.е.
, члены которого больше соответствующих членов исследуемого ряда, т.е.  . Ряд
. Ряд  составлен из членов бесконечной убывающей геометрической прогрессии (знаменатель прогрессии q =
составлен из членов бесконечной убывающей геометрической прогрессии (знаменатель прогрессии q =  < 1) и, следовательно, сходится. Тогда согласно первому признаку сравнения исследуемый ряд сходится.
< 1) и, следовательно, сходится. Тогда согласно первому признаку сравнения исследуемый ряд сходится. (аn > 0, bn > 0) при n, стремящемся к бесконечности, т. е.
(аn > 0, bn > 0) при n, стремящемся к бесконечности, т. е. 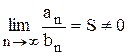 (S = const), то оба ряда в смысле сходимости ведут себя одинаково.
(S = const), то оба ряда в смысле сходимости ведут себя одинаково. .
. с гармоническим рядом
с гармоническим рядом 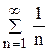 , общий член которого
, общий член которого  .
. .
. .
. .
. ,
, < 1.
< 1. .
. .
. и предел этой дроби при n ® ¥ легко вычисляется:
и предел этой дроби при n ® ¥ легко вычисляется: < 1.
< 1. и f(x) – непрерывная, положительная, монотонно убывающая функция такая, что f(n) = an, где n Î [m; +¥). Тогда данный ряд сходится или расходится одновременно с несобственным интегралом
и f(x) – непрерывная, положительная, монотонно убывающая функция такая, что f(n) = an, где n Î [m; +¥). Тогда данный ряд сходится или расходится одновременно с несобственным интегралом  .
. (a > 0).
(a > 0). , m = 1. Тогда
, m = 1. Тогда

 ; 20.
; 20.  ; 21.
; 21.  ;
; ; 23.
; 23.  ; 24.
; 24.  ;
; ; 26.
; 26.  ; 27.
; 27.  .
. ; 29.
; 29.  ; 30.
; 30.  ;
; ; 32.
; 32.  ; 33.
; 33.  ;
; ; 35.
; 35.  ; 36.
; 36. 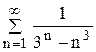 .
. ; 38.
; 38.  ;
; ; 40.
; 40. 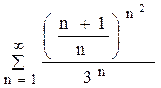 .
. ; 42.
; 42.  ; 43.
; 43.  ;
; ; 45.
; 45.  ; 46.
; 46.  .
. ; 48.
; 48.  ; 49.
; 49.  ;
; ; 51.
; 51. 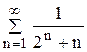 ; 52.
; 52.  ;
; ; 54.
; 54.  ; 55.
; 55.  ;
; ; 57.
; 57.  ; 58.
; 58.  ;
; ; 60.
; 60.  ; 61.
; 61.  .
. (6.4)
(6.4)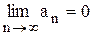 .
. …
… ,
,
 .
.