
|
|
Определение определенного интегралаГлава IV. ИНТЕГРИРОВАНИЕ Первообразная и неопределенный интеграл Основные понятия Определение 1. Функция F(x) называется первообразной для функции f(x) на некотором промежутке, если в любой точке этого промежутка выполняется равенство Если F(x) - первообразная для f(x), то функция F(x) + C, где C – некоторая постоянная, также является первообразной для функции f(x), так как Определение 2. Если F(x) - первообразная для функции f(x), то множество функций F(x) + C, где С – произвольная постоянная, называется неопределенным интегралом от функции f(x) и обозначается Согласно данному определению имеем
При этом f(x) называется подынтегральной функцией, f(x) dx – подынтегральным выражением, x - переменной интегрирования. 2. Основные свойства неопределенного интеграла 1. 2. d 3. 4. 5.
3. Таблица основных интегралов 1. 3.
5.
7. 9. 11. 13.
Методы интегрирования 1. Непосредственным интегрированием называется вычисление интегралов с помощью таблицы основных интегралов и основных свойств неопределенных интегралов. Пример 1. Вычислить интеграл
Решение. Применим свойства 4и5и воспользуемся таблицей интегралов, тогда
Пример 2. Вычислить интеграл Решение. Интеграл не табличный, поэтому преобразуем его. Так как 1 = sin2x + cos2x, то интеграл можно записать в виде
Применяя свойство 5, получим
Получили два табличных интеграла 8 и 9.
Пример 3. Вычислить интеграл Решение. Интеграл не табличный. Умножим и разделим подынтегральное выражение на 3 и учтем, что 3dx = d(3x), тогда
Мы привели исходный интеграл к табличному интегралу 7 с переменной интегрирования 3x
Пример 4. Вычислить интеграл Решение. Данный интеграл может быть приведен к табличному, если учесть, что cos x dx =
Пример 5. Вычислить интеграл Решение. Учитывая, что dx = d(1 + x), получим
Пример 6. Вычислить интеграл
Решение. Так как xdx =
Пример 7. Вычислить интеграл Решение. Так как 1 + 2x2 = (1 + x2) + x2, то
= По формулам 2 и 11 таблицы интегралов получаем
2. Метод подстановки (замены переменной) Замена переменной интегрирования в неопределенном интеграле производится с помощью подстановки двух видов: 1) x = j(t), где j(t) - дифференцируемая функция новой переменной t. Формула замены переменной в этом случае имеет вид
2) u = y(x), где u – новая переменная. Формула замены переменной при такой подстановке:
Пример 8.Вычислить интеграл Решение. Сделаем подстановку t =
Вернемся к переменной интегрирования x. Подставляя в результат интегрирования t =
Пример 9. Вычислить интеграл Решение. Положим x3+ 5 = t, тогда 3x2dx = dt, x2dx =
Если интеграл Пример 10. Вычислить интеграл Решение. Пусть ax + b = t, тогда аdx = dt, dx = Пример 11. Вычислить интеграл Решение. Сделаем подстановку cos2x = t, тогда 2 cos x sin x dx = dt, т. е. sin 2x dx = -dt. Тогда
= -arcsin Пример 12. Вычислить интеграл Решение. Преобразуя знаменатель дроби, получим x4+ 2x2+ 5 = (x2+ 1)2+ 4. Сделаем подстановку x2+ 1 = t, тогда xdx =
Вычислить интегралы
1. 3. 5. 7. 9. 11. 13. 15. 17. 19. 21. 23. 25. 27. 29. 31. 33. 35. 37. 39.
3. Метод интегрирования по частям Интегрированием по частямназывается вычисление интеграла по формуле
где u и v – дифференцируемые функции от х. Данная формула позволяет свести вычисление интеграла
Так, например 1. Для интегралов вида
где P(x) – многочлен, а - число, полагают u = P(x), а все остальные сомножители – dv. 2. В интегралах вида
полагают Р(x)dx = dv, а остальные сомножители – u. 3. В интегралах вида
за u можно принять любую из функций eaxили sin bx (или cos bx). Пример 13. Вычислить интеграл Решение. Положим u = x, dv = du = dx, v = По формуле интегрирования по частям, имеем
Пример 14. Вычислить интеграл Решение. Положим dv = x2dx, ln x = u, тогда v =
Пример 15. Вычислить интеграл I= Решение. Пусть u = ex, dv = sin x dx, тогда du = exdx, v = Следовательно, I = -excos x + Полученный интеграл проинтегрируем также по частям, положив u = ex, dv = cos x dx, тогда du = exdx и v = Применив дважды операцию интегрирования по частям, мы в правой части получили исходный интеграл. Таким образом, приходим к уравнению с неизвестным интегралом I. 2I = -excos x + exsin x, I =
Вычислить интегралы
41. 43. 45. 47. 49. 51. 53. 55.
Определенный интеграл Определение определенного интеграла Пусть функция f(x) определена на отрезке [a; b], a < b. Разобьем этот отрезок на n произвольных частей точками а = x0 < x1 < x2 < … < < xi-1 < xi < … < xn = b. В каждом элементарном отрезке [xi-1; xi] выберем произвольную точку x (xi-1 £ x £ xi) и обозначим через Dxi = xi - xi-1 длину каждого такого отрезка. Тогда сумма вида
называется интегральной суммой для функции f(x) на [a; b]. Обозначим через l длину наибольшего элементарного отрезка разбиения: l = mаx{Dxi}. Определение 1.Определенным интегралом от функции f(x) на отрезке [a; b] называется предел интегральной суммы при l®0, т.е.
Здесь числа a и b называются нижним и верхним пределами интегрирования соответственно. Для существования определенного интеграла от функции f(x) на отрезке [a; b], достаточно ее непрерывности на этом отрезке. Определенный интеграл
2. Основные свойства определенного интеграла 1. Определенный интеграл с одинаковыми пределами равен нулю:
2. При перестановке пределов интегрирования определенный интеграл меняет знак на противоположный:
3. Постоянный множитель можно выносить за знак определенного интеграла:
4. Определенный интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме их интегралов:
5. Отрезок интегрирования можно разбивать на части:
Замечание. Определенный интеграл от нечетной функции по симметричным пределам равен нулю.
3. Формула Ньютона-Лейбница Если функция f(x) непрерывна на отрезке [a; b] и функция F(x) является некоторой ее первообразной на этом отрезке, то определенный интеграл может быть вычислен по формуле Ньютона-Лейбница
Пример 1. Вычислить интегралы 1. Решение. Используя формулу Ньютона-Лейбница получим 1. 2. -
Вычислить интегралы
57. 59. 61. 63. 65. 67. 69. 71. 73. 75.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 или dF(x) = f(x) dx.
или dF(x) = f(x) dx. для любого С.
для любого С. .
. .
. .
. .
. .
.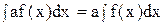 , a = const.
, a = const. .
. 2.
2. 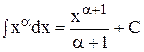 (a ¹ -1)
(a ¹ -1) (x ¹ 0) 4.
(x ¹ 0) 4. 
 6.
6. 
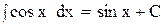 8.
8. 
 10.
10. 
 = arctgx + C 12.
= arctgx + C 12. 
 14.
14. 

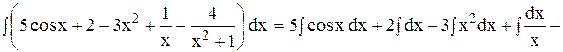
 .
.
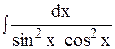 =
=  .
.
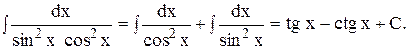

 .
. .
.
 Считая sin x переменной интегрирования, по формуле 2 таблицы интегралов получим
Считая sin x переменной интегрирования, по формуле 2 таблицы интегралов получим

 .
.
 , то
, то .
.

 .
.
 ;
; .
.
 , т. е. x = t3. Эта подстановка приведет к тому, что под знаком синуса окажется переменная интегрирования, а не корень из нее. Найдем дифференциал dx =
, т. е. x = t3. Эта подстановка приведет к тому, что под знаком синуса окажется переменная интегрирования, а не корень из нее. Найдем дифференциал dx =  = 3t2dt. Тогда получим
= 3t2dt. Тогда получим .
. .
.
 и интеграл преобразуется к виду
и интеграл преобразуется к виду .
. является табличным, то интеграл
является табличным, то интеграл  может быть легко найден с помощью подстановки ax + b = t.
может быть легко найден с помощью подстановки ax + b = t.
 и интеграл примет вид
и интеграл примет вид  .
. .
.
 .
. .
. . Отсюда
. Отсюда .
. 2.
2. 
 4.
4. 
 6.
6. 
 8.
8. 
 10.
10. 
 12.
12. 
 14.
14. 
 16.
16. 
 18.
18. 
 20.
20. 
 22.
22. 
 24.
24. 
 26.
26. 
 28.
28. 
 30.
30. 
 32.
32. 
 34.
34. 
 36.
36. 
 38.
38. 
 40.
40. 
 ,
, к вычислению
к вычислению 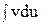 . Ее применение целесообразно в тех случаях, когда последний интеграл либо проще исходного, либо ему подобен. При этом за u берется такая часть подынтегральной функции, которая при дифференцировании упрощается, а за dv – та часть подынтегрального выражения, интеграл от которой известен или может быть найден.
. Ее применение целесообразно в тех случаях, когда последний интеграл либо проще исходного, либо ему подобен. При этом за u берется такая часть подынтегральной функции, которая при дифференцировании упрощается, а за dv – та часть подынтегрального выражения, интеграл от которой известен или может быть найден. ,
,  ,
,  ,
, ,
, 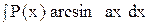 ,
,  ,
, ,
, 
 ,
, 
 .
. , тогда
, тогда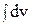 =
=  , т. е. v = -cos x.
, т. е. v = -cos x. .
.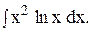
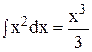 , du =
, du =  и
и .
. .
. .
. .
. и следовательно I = -excos x + (еxsin x -
и следовательно I = -excos x + (еxsin x -  .
. 42.
42. 
 44.
44. 
 46.
46. 
 48.
48. 
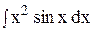 50.
50. 
 52.
52. 
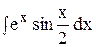 54.
54. 
 56.
56. 

 =
=  .
. численно равен площади S криволинейной трапеции, ограниченной графиком функции f(x), осью абсцисс и прямыми x = a и x = b, т. е. S =
численно равен площади S криволинейной трапеции, ограниченной графиком функции f(x), осью абсцисс и прямыми x = a и x = b, т. е. S =  . В этом заключается геометрический смысл определенного интеграла.
. В этом заключается геометрический смысл определенного интеграла. .
. .
. .
. .
. сÎ[a; b].
сÎ[a; b]. .
. ; 2.
; 2.  .
. ;
;
 .
. (n¹1) 58.
(n¹1) 58. 
 60.
60. 
 62.
62. 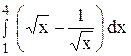
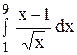 64.
64. 
 66.
66. 
 68.
68. 
 70.
70. 
 72.
72. 
 74.
74. 
 76.
76. 