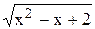|
|
Приложение дифференциала к приближенным вычислениям12 Приближенное значение приращения функции При достаточно малых Dy » Пример 2. Найти приближенное значение приращения функции y= Решение. Воспользуемся формулой (2.3). Для этого вычислим
Dу » Приближенное значение функции в точке В соответствии с определением приращения функции y = f(x) в точке x0 при приращении аргумента Dx (Dx®0) Dy = f(x0 + Dx) - f(x0) и формулой (3.3) можно записать f(x0 + Dx) » f(x0) + Частными случаями формулы (3.4) являются выражения: (1 + Dx)n» 1 + nDx (3.4a) ln(1 + Dx) » Dx (3.4б) sinDx » Dx (3.4в) tgDx » Dx (3.4г) Здесь, как и ранее предполагается, что Dx®0. Пример 3. Найти приближенное значение функции f(x) = (3x -5)5в точке x1=2,02. Решение. Для вычислений воспользуемся формулой (3.4). Представим x1 в виде x1 = x0 + Dx. Тогда x0 = 2, Dx = 0,02. f(2,02)=f(2 + 0,02) » f(2) + f(2) = (3 × 2 - 5)5= 1
f(2,02) = (3 × 2,02 - 5)5 » 1 + 15 × 0,02 = 1,3 Пример 4. Вычислить (1,01)5, Решение 1. Воспользуемся формулой (3.4а). Для этого представим (1,01)5в виде (1+0,01)5. Тогда, полагая Dх = 0,01, n = 5, получим (1,01)5= (1 + 0,01)5 » 1 + 5 × 0,01 = 1,05. 2. Представив
3. Учитывая, что ln(1,02) = ln(1 + 0,02) и полагая Dx=0,02, по формуле (3.4б) получим ln(1,02) = ln(1 + 0,02) » 0,02. 4. Аналогично ln
Найти приближенные значения приращения функций 155. y = 2x3+ 5 при изменении аргумента x от значения x0 = 2 до x1 = 2,001 156. у = 3x2+ 5x + 1 при x0 = 3 и Dx = 0,001 157. y = x3 + x - 1 при x0 = 2 и Dx = 0,01 158. y = ln x при x0 = 10 и Dx = 0,01 159. y = x2 - 2x при x0 = 3 и Dx = 0,01
Найти приближенные значения функций 160. у = 2x2- x + 1 в точке x1 = 2,01 161. y = x2+ 3x + 1 в точке x1 = 3,02 162. y = 163. y= 164. y = 165. y = sin 2x в точке x1 = 0,015
Вычислить приближенно
166. (1,025)10 167. (9,06)2 168.(1,012)3 169. (9,95)3 170. (1,005)10 171. (0,975)4 172. 175. 178. ln(1,003×e) 179. ln(1,05)5 180. ln 181. ln0,98 182. ln
Исследование функций и построение графиков Признаки монотонности функции Теорема 1 (необходимое условие возрастания (убывания) функции). Если дифференцируемая функция y = f(x), xÎ(a; b) возрастает (убывает) на интервале (a; b), то Теорема 2 (достаточное условие возрастания (убывания) функции). Если функция y = f(x), xÎ(a; b) имеет положительную (отрицательную) производную в каждой точке интервала (a; b), то эта функция возрастает (убывает) на этом интервале.
Экстремумы функции Определение 1. Точка x0 называется точкой максимума (минимума) функции у = f(x), если для всех x из некоторой d-окрестности точки x0 выполняется неравенство f(x) < f(x0) (f(x) > f(x0)) при x ¹ x0. Теорема 3 (Ферма) (необходимое условие существования экстремума). Если точка x0 является точкой экстремума функции y = f(x) и в этой точке существует производная Теорема 4 (первое достаточное условие существования экстремума). Пусть функция y = f(x) дифференцируема в некоторой d-окрестности точки x0. Тогда: 1) если производная 2) если производная 3) если производная Определение 2. Точки, в которых производная функции обращается в нуль или не существует, называются критическими точками первого рода.
Алгоритм нахождения экстремума функции с помощью первой производной 1. Найти область определения D(f) функции у = f(x). 2. Вычислить первую производную 3. Найти критические точки первого рода. 4. Расставить критические точки в области определения D(f) функции y = f(x) и определить знак производной 5. Выделить точки максимума и минимума функции и вычислить в этих точках значения функции.
Пример 1. Исследовать на экстремум функцию у = x3- 3x2. Решение. В соответствии с алгоритмом нахождения экстремума функции с помощью первой производной имеем: 1. D(f): xÎ(-¥; ¥). 2. 3. 4.
0 2 х
5. ymax= f(0) = 03 × 3 × 02 = 0. Координаты максимума (0; 0). ymin= f(2) = 23 - 3 × 22= -4. Координаты минимума (2; -4). Теорема 5 (второе достаточное условие существования экстремума). Если функция у = f(x) определена и дважды дифференцируема в некоторой окрестности точки x0, причем
Алгоритм нахождения экстремума функции с помощью второй производной 1. Найти область определения D(f) функции y = f(x). 2. Вычислить первую производную 3. Найти критические точки первого рода. 4. Вычислить вторую производную 5. Определить знак второй производной в каждой из критических точек. 6. Вычислить максимальное и минимальное значение функций.
Пример 2. Исследовать на экстремум функцию f(x) = x3- 9x2+ 24x - 12. Решение. В соответствии с алгоритмом нахождения экстремума функции с помощью второй производной, имеем: 1. D(f): xÎ(-¥; ¥). 2. 3. 4. 5.
6. ymax= f(x = 2) = 23- 9 × 22+ 24 × 2 - 12 = 8 max(2; 8). ymin= f(x = 4) = 43- 9 × 42+ 24 × 4 - 12 = 4 min(4; 4).
С помощью первой производной исследовать на экстремум функции:
184. f(x) = x2– x 185. f(x) = -x2- x 186. f(x) = x2– 8x + 12 187. f(x) = x2– 4x + 3 188. f(x) = 2x4- x 189. f(x) = 190. f(x) = 5 - 2 192. f(x) = ex+ e-x 193. f(x) = x2 e-x 194. f(x) = x - 2 ln x 195. f(x) = x ln x 196. f(x) =
С помощью второй производной исследовать на экстремум функции:
198. f(x) = 2x2- 3 199. f(x) = x2- 2x 200. f(x) = -x2+ 4x 201. f(x) = -x2+ x + 6 202. f(x) = 204. f(x) = x4+ 3x2- 4 205. f(x) = x3 - 206. f(x) = 208. f(x) = 210. f(x) = x (ln x - 2) 211. f(x) = x ln2x + x + 4

12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 приращение функции приближенно равно ее дифференциалу, т.е. Dy » dy и, следовательно,
приращение функции приближенно равно ее дифференциалу, т.е. Dy » dy и, следовательно, . (3.3)
. (3.3) при изменении аргумента x от значения x0=3 до x1=3,01.
при изменении аргумента x от значения x0=3 до x1=3,01.

 .
. . (3.4)
. (3.4)

 = 15 × (3 × 2 - 5)4= 15
= 15 × (3 × 2 - 5)4= 15 , ln(1,02), ln
, ln(1,02), ln  .
. (1 - 0,006)1/6 » 1 +
(1 - 0,006)1/6 » 1 + 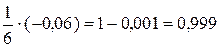 .
.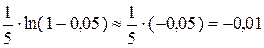 .
.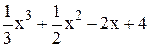 в точке x1 = 1,1
в точке x1 = 1,1 в точке x1 = 3,032
в точке x1 = 3,032 в точке x1 = 3,97
в точке x1 = 3,97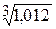 173.
173.  174.
174. 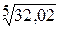
 176.
176.  177.
177. 

 183. ln(e2×0,97)
183. ln(e2×0,97) для любого x0Î(a; b).
для любого x0Î(a; b). , то
, то 
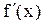 при переходе через точку x0 меняет знак с (+) на (-), то x0 является точкой максимума;
при переходе через точку x0 меняет знак с (+) на (-), то x0 является точкой максимума; при переходе через точку x0 не меняет знак, то в точке x0 функция не имеет экстремума.
при переходе через точку x0 не меняет знак, то в точке x0 функция не имеет экстремума.
 .
. 3x2- 6x = 0 Þ x = 0, x = 2 - критические точки первого рода.
3x2- 6x = 0 Þ x = 0, x = 2 - критические точки первого рода.




 max min
max min + - +
+ - + Производная при переходе чрез точку x = 0
Производная при переходе чрез точку x = 0 меняет знак с (+) на (-), следовательно это точка
меняет знак с (+) на (-), следовательно это точка максимума. При переходе через точку х = 2
максимума. При переходе через точку х = 2 
 , то в точке x0 функция f(x) имеет максимум, если
, то в точке x0 функция f(x) имеет максимум, если  и минимум, если
и минимум, если  .
.
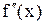 .
. .
. 3x2 - 18x + 24 = 0 Þ x = 2, x = 4 - критические точки первого рода.
3x2 - 18x + 24 = 0 Þ x = 2, x = 4 - критические точки первого рода. 6x - 18.
6x - 18. 6 × 2 - 18 = -6 < 0 Þ x = 2 – точка максимума.
6 × 2 - 18 = -6 < 0 Þ x = 2 – точка максимума. 6 × 4 - 18 = 6 > 0 Þ x = 4 - точка минимума.
6 × 4 - 18 = 6 > 0 Þ x = 4 - точка минимума.
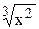 191. f(x) = 3
191. f(x) = 3 
 197. f(x) =
197. f(x) = 
 203. f(x) =
203. f(x) = 
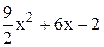
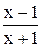 207. f(x) = x +
207. f(x) = x + 
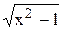 209. f(x) =
209. f(x) =