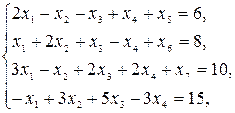|
|
Задача линейного программированияЗадача линейного программирования Понятие линейного программирования Линейное программирование — раздел математического, применяемый при разработке методов отыскания экстремума линейных функций нескольких переменных при линейных дополнительных ограничениях, налагаемых на переменные. По типу решаемых задач его методы разделяются на универсальные и специальные. С помощью универсальных методов могут решаться любые задачи линейного программирования (ЗЛП). Специальные методы учитывают особенности модели задачи, ее целевой функции и системы ограничений. Особенностью задач линейного программирования является то, что экстремума целевая функция достигает на границе области допустимых решений. Классические же методы дифференциального исчисления связаны с нахождением экстремумов функции во внутренней точке области допустимых значений. Отсюда — необходимость разработки новых методов. Примеры экономических задач линейного программирования Задача о наилучшем использовании ресурсов
Пусть - некоторая производственная единица (цех, завод, объединение и т. д.), исходя из конъюнктуры рынка, технических или технологических возможностей и имеющихся ресурсов, может выпускать п различных видов продукции (товаров), известных под номерами, обозначаемыми индексом j (j= Предприятие при производстве этих видов продукции должно ограничиваться имеющимися видами ресурсов, технологий, других производственных факторов (сырья, полуфабрикатов, рабочей силы, оборудования, электроэнергии и т. д.). Все эти виды ограничивающих факторов называют ингредиентами Ri. Пусть их число равно m; припишем им индекс i (i= Известна экономическая выгода (мера полезности) производства продукции каждого вида, исчисляемая, скажем, по отпускной цене товара, его прибыльности, издержкам производства, степени удовлетворения потребностей и т. д. Примем в качестве такой меры, например, цену реализации сj (j= Известны также технологические коэффициенты аij, которые указывают, сколько единиц i-горесурса требуется для производства единицы продукции j-го вида. Матрицу коэффициентов аij называют технологической и обозначают буквой А. Имеем А= Обозначим через х=(x1; ...; хj; ...; хп) план производства, показывающий, какие виды товаров П1, …,Пj, …,Пn нужно производить и в каких количествах, чтобы обеспечить предприятию максимум объема реализации при имеющихся ресурсах. Так как сj — цена реализации единицы j-й продукции, цена реализованных хj единиц будет равна cjxj, а общий объем реализации Z=c1x1+…+cnxn Это выражение — целевая функция, которую нужно максимизировать. Так как aijxj — расход i-го ресурса на производство хj единиц j-й продукции, то, просуммировав расход i-го ресурса на выпуск всех n видов продукции, получим общий расход этого ресурса, который не должен превосходить bi (i= ai1x1+…+aijxj+…+ainxn ≤ bi. Чтобы искомый план х = (x1; x2; …; xj; …; xn) был реален, наряду с ограничениями на ресурсы нужно наложить условие неотрицательности на объемы хj выпуска продукции: xj ≥0(j= Таким образом, модель задачи о наилучшем использовании ресурсов примет вид: найти max Z= при ограничениях:
xj ≥ 0 (j= Так как переменные xj входят в функцию z(х) и систему ограничений только в первой степени, а показатели аij, bi, сj являются постоянными в планируемый период, то (1) — (З) —задача линейного программирования.
Транспортная задача
Рассмотрим простейший вариант модели транспортной задачи, когда речь идет о рациональной перевозке некоторого однородного продукта от производителей к потребителям; при этом имеется баланс между суммарным спросом потребителей и возможностями поставщиков по их удовлетворению. Причем потребителям безразлично, из каких пунктов производства будет поступать продукция, лишь бы их заявки были полностью удовлетворены. Так как от схемы прикрепления потребителей к поставщикам существенно зависит объем транспортной работы, возникает задача о наиболее рациональном прикреплении, правильном направлении перевозок грузов, при котором потребности полностью удовлетворяются, вся продукция от поставщиков вывозится, а затраты на транспортировку минимальны.
Задача формулируется так. Имеется m пунктов производства Известны величины cij — затраты на перевозку единицы продукта из i-го пункта производства в j-й пункт потребления, где С целью удобства построения математической модели матрицы тарифов и перевозок совмещают в одну, именуемую макетом транспортной задачи (см. лекцию №3). Математическая модель транспортной задачи: целевая функция, описывающая транспортные затраты, Z= минимизируется при ограничениях: на возможности поставщиков — весь продукт из пунктов производства должен быть вывезен:
на спрос потребителей, который должен быть удовлетворен:
при условии неотрицательности переменных, исключающем обратные перевозки: xij =0 (i=1,…,m; j=1,…,n) (4). Задача линейного программирования Определение. Общей задачей линейного программирования называется задача, которая состоит в определении максимального (минимального) значения функции F= при условиях
где aij, bi, cj — заданные постоянные величины и k≤m. Определение. Функция (1) называется целевой функцией (или линейной формой) задачи (1) — (4), а условия (2) — (4) — ограничениями данной задачи. Определение. Стандартной (или симметричной) задачей линейного программирования называется задача, которая состоит в определении максимального значения функции (1) при выполнении условий (2) и (4), где k=m и i=n. Определение. Канонической (или основной) задачейлинейного программирования называется задача, которая состоит в определении максимального значения функции (1) при выполнении условий (3) и (4), где k=0 и i=n. Определение. Совокупность чисел X=(x1, x2, ...., xn), удовлетворяющих ограничениям задачи (2) — (4), называется допустимым решением (или планом). Определение. План X*=(x*1, x*2, ...., x*n), при котором целевая функция задачи (1) принимает свое максимальное (минимальное) значение, называется оптимальным.
Значение целевой функции (1) при плане X будем обозначать через F(X). Следовательно, X*— оптимальный план задачи, если для любого X выполняется неравенство F(X) ≤ F (X*) [соответственно F(X)≥F (X*)].
Указанные выше три формы задачи линейного программирования эквивалентны в том смысле, что каждая из них с помощью несложных преобразований может быть переписана в форме другой задачи. Это означает, что если имеется способ нахождения решения одной из указанных задач, то тем самым может быть определен оптимальный план любой из трех задач. Чтобы перейти от одной формы записи задачи линейного программирования к другой, нужно в общем случае уметь, во-первых, сводить задачу минимизации функции к задаче максимизации, во-вторых, переходить от ограничений-неравенств к ограничениям-равенствам и наоборот, в-третьих, заменять переменные, которые не подчинены условию неотрицательности. В том случае, когда требуется найти минимум функции F = c1x1+c2x2+…+cnxn, можно перейти к нахождению максимума функции F1= -F= =-c1x1-c2x2-…-cnxn, поскольку min F=-max(-F). Ограничение-неравенство исходной задачи линейного программирования, имеющее вид « ≤», можно преобразовать в ограничение-равенство добавлением к его левой части дополнительной неотрицательной переменной, а ограничение-неравенство вида « ≥» — в ограничение-равенство вычитанием из его левой части дополнительной неотрицательной переменной. Таким образом, ограничение-неравенство ai1x1+ai2x2+…+ainxn ≤ bi преобразуется в ограничение-равенство ai1x1+ai2x2+…+ainxn +xn+1= bi (xn+1≥0),(5) а ограничение-неравенство ai1x1+ai2x2+…+ainxn ≥ bi — в ограничение-равенство ai1x1+ai2x2+…+ainxn -xn+1= bi (xn+1≥0). (6) В то же время каждое уравнение системы ограничений ai1x1+ai2x2+…+ainxn =bi можно записать в виде неравенств:
Число вводимых дополнительных неотрицательных переменных при преобразовании ограничений-неравенств в ограничения-равенства равно числу преобразуемых неравенств. Вводимые дополнительные переменные имеют вполне определенный экономический смысл. Так, если в ограничениях исходной задачи линейного программирования отражается расход и наличие производственных ресурсов, то числовое значение дополнительной переменной в плане задачи, записанной в форме основной, равно объему неиспользуемого соответствующего ресурса. Отметим, наконец, что если переменная xk не подчинена условию неотрицательности, то ее следует заменить двумя неотрицательными переменными uk и vk, приняв xk = uk - vk.
Задача. Записать в форме основной задачи линейного программирования следующую задачу: найти максимум функции F = 3х1—2x2—5x4+ x5 при условиях
x1, x2, x3, x4, x5 ≥ 0.
Решение. В данной задаче требуется найти максимум функции, а система ограничений содержит четыре неравенства. Следовательно, чтобы записать ее в форме основной задачи, нужно перейти от ограничений-неравенств к ограничениям-равенствам. Так как число неравенств, входящих в систему ограничений задачи, равно четырем, то этот переход может быть осуществлен введением четырех дополнительных неотрицательных переменных. При этом к левым частям каждого из неравенств вида «≤» соответствующая дополнительная переменная прибавляется, а из левых частей каждого из неравенств вида «≥» вычитается. В результате ограничения принимают вид уравнений:
x1, x2, …, x9 ≥ 0. Следовательно, данная задача может быть записана в форме основной задачи таким образом: максимизировать функцию F = 3х1—2x2—5x4+ x5 при условиях
x1, x2, …, x9 ≥ 0.
Задача.Записать задачу, состоящую в минимизации функции F = -x1+2x2-x3+x4 при условиях
x1, x2, x3, x4 ≥ 0. в форме основной задачи линейного программирования. Решение. В данной задаче требуется найти минимум целевой функции, а система ограничений содержит три неравенства. Следовательно, чтобы записать ее в форме основной задачи, вместо нахождения минимума функции F нужно найти максимум функции F=—F при ограничениях, получающихся из ограничений исходной задачи добавлением к левым частям каждого из ограничений-неравенств вида «≤» дополнительной неотрицательной переменной и вычитанием дополнительных переменных из левых частей каждого из ограничений-неравенств вида «≥». Следовательно, исходная задача может быть записана в форме основной задачи линейного программирования так: найти максимум функции F1= x1— 2x2 + x3 — x4 при условиях
x1, x2, …, x7 ≥ 0.
Задача.Записать в форме стандартной задачи линейного программирования следующую задачу: найти максимум функции F = 6,5x1 — 7,5x3+ 23,5x4 — 5x5 при условиях
x1, x2, …, x5 ≥ 0. Решение. Методом последовательного исключения неизвестных сведем данную задачу к следующей: найти максимум функции F = 6,5x1 — 7,5x3+ 23,5x4 — 5x5 при условиях
x1, x2, …, x5 ≥ 0. Последняя задача записана в форме основной для задачи, состоящей в нахождении максимального значения функции F=x3+2x4 при условиях
x3, x4 ≥ 0 Целевая функция задачи преобразована с помощью подстановки вместо x1 и x5 их значений в соответствии с уравнениями системы ограничений задачи. Библиография 1. Кузнецов Ю.Н., Кузубов В.И., Волощенко А.Б., Математическое программирование, М.: Высшая школа, 1980. 2. Акулич И.Л. Математическое программирование в примерах и задачах, М.: Высшая школа, 1986. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 ). Ее будем обозначать Пj.
). Ее будем обозначать Пj.  ). Они ограничены, и их количества равны соответственно b1 ,.., bi, .., bm условных единиц. Таким образом, b=(b1 ; ..; bi; .. ; bm)—вектор ресурсов.
). Они ограничены, и их количества равны соответственно b1 ,.., bi, .., bm условных единиц. Таким образом, b=(b1 ; ..; bi; .. ; bm)—вектор ресурсов. .
. (1)
(1) (2)
(2) с запасами
с запасами  единиц однородного продукта. Этот продукт нужно доставить n потребителям
единиц однородного продукта. Этот продукт нужно доставить n потребителям  с потребностями
с потребностями  единиц. Причем
единиц. Причем 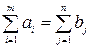 .
. . Обозначим через xij количество продукта, перевозимое из i-го пункта производства в j-й пункт потребления. Матрица
. Обозначим через xij количество продукта, перевозимое из i-го пункта производства в j-й пункт потребления. Матрица  называется матрицей тарифов,
называется матрицей тарифов,  — матрицей перевозок.
— матрицей перевозок. (1)
(1) (i=1,…,m) ( 2)
(i=1,…,m) ( 2) (j=1,…,n) (3)
(j=1,…,n) (3) . (1)
. (1) , (2)
, (2) (3)
(3) (
(  ), (4)
), (4) (7)
(7)