
|
|
Формулы логики высказываний. Равносильности формул12 Пусть дана некоторая совокупность высказываний. С помощью логических операций над ними можно строить различные сложные высказывания. Всякое сложное высказывание, которое можно получить из элементарных применением логических операций называется формулой логики. В формуле логики очень важен порядок расстановки скобок, так как две формулы, отличающиеся друг от друга только расстановкой скобок, могут иметь разные значения истинности при одинаковых значениях истинности, входящих в них простых высказываний. Например, пусть Ф1 – это формула (A Ú B) ® (C Ù B), Ф2 – это формула (A Ú (B ® C)) Ù B. Пусть A – ложно, B – ложно, C – истинно. Тогда Ф1 – истинно, Ф2 – ложно. В сложных логических формулах, содержащих много связок, некоторые скобки принято опускать. Аналогичная ситуация имеет место с вычислением значений числовых выражений. Например, рассмотрим числовое выражение 4 × 52 + 20 : 7 – 353 : 16. Оно не содержит ни одной скобки, но мы однозначно можем сказать, в каком порядке следует выполнять действия в этом выражении. Напомним, что самым «сильным» является действие возведения в степень, оно всегда выполняется первым. Затем идут действия умножения и деления, а самыми «слабыми» являются сложение и вычитание, они выполняются в последнюю очередь. То же самое имеет место и с логическими формулами: самой «сильной» логической связкой является отрицание, затем идут связки конъюнкции и дизъюнкции, а самыми «слабыми» являются связки импликации и эквиваленции. Логическое значение формулы математической логики полностью определяется логическими значениями входящих в нее элементарных высказываний. Все возможные значения формулы могут быть описаны полностью с помощью таблицы истинности. Опишем алгоритм построения таблицы истинности для составного высказывания: 1) подсчитать количество элементарных высказываний, входящих в формулу (обозначим это количество – n); 2) определить число строк в таблице (оно равно 2n); 3) подсчитать количество логических связок в выражении и определить количество столбцов в таблице, равное n плюс количество логических связок. 4) записать названия столбцов таблицы: сначала обозначения элементарных высказываний, затем, в соответствии с последовательностью их выполнения, обозначения логических операций с учетом скобок и приоритетов. 5) заполнить столбцы элементарных высказываний наборами значений: а) разделить первый столбец пополам и заполнить верхнюю часть колонки значениями «И», а нижнюю – «Л»; б) разделить второй столбец на 4 части и заполнить каждую четверть чередующимися группами «И» и «Л»; в) продолжать деление следующих столбцов, соответствующих значениям элементарных высказываний, на 8, 16 и т.д. частей и заполнение их группами «И» и «Л» до тех пор, пока эти группы не будут состоять из одного символа; 6) провести заполнение таблицы истинности по столбцам, выполняя логические операции в соответствии с установленной ранее последовательностью. Например, построим таблицу истинности для формулы
В логике высказываний существуют формулы, которые принимают одинаковые значения истинности (И или Л) при всех значениях истинности входящих в них простых высказываний. Такие формулы получили специальные названия, так как имеют большое значение в этой теории. Определение. Формула называется тавтологией или тождественно истинной формулой, если при любых значениях истинности входящих в нее простых высказываний, ее значение истинно. Например, формула A ® (B ® A) является тавтологией. Действительно, рассмотрим таблицу истинности этой формулы:
Определение. Формула называется противоречием или тождественно ложной формулой, если при любых значениях истинности входящих в нее простых высказываний, ее значение ложно. Предложение: Формула Ф является тавтологией тогда и только тогда, когда формула Доказательство непосредственно следует из определений отрицания и тавтологий. Определение. Две формулы алгебры логики называются равносильными, если они принимают одинаковые значения при любом наборе значений входящих в формулы элементарных высказываний. Для доказательства равносильности двух формул достаточно составить их таблицы истинности и убедиться, что они совпадают. В логике высказываний существуют основные равносильные формулы, которые называют законами логики высказываний: 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. Для доказательства этих законов достаточно составить таблицы истинности соответствующих формул. В каждой сложной формуле можно выделить более простые подформулы. Определение. Подформулой называется такая часть формулы, которая сама является формулой. Если подформулу заменить на равносильную ей формулу, то полученная формула будет равносильной исходной. Этот факт используется для доказательства равносильности формул, упрощения формул, решения логических задач и др. Например,
Таким образом, Предикаты и кванторы
Не все предложения, используемые как в математике, так и в реальной жизни, являются высказываниями. Например, возьмем в руки бланк какой-либо справки. Даже если на этом бланке есть все подписи и печати, она не будет являться документом, пока не вписаны фамилия, имя и отчество того, кому выдана эта справка. аналогичная ситуация имеет место и в математике. Например, предложения типа «целое число x – четно», «2x + 1 < 0», «x2 + y2 = 25» и др. Эти предложения не являются высказываниями. Но если вместо переменных, входящих в это предложение, мы подставим их конкретные значения, то получим высказывания, истинные или ложные. Например, «целое число 5 – четно» – ложное высказывание, «2 × (– 5) + 1 < 0» – истинное высказывание, «32 + 42 = 25» – истинное высказывание. Определение. Предложение с переменными, которое после замены переменных определенными их значениями превращается в высказывание, называется предикатом. Предикаты будем обозначать большими латинскими буквами P, Q и др., в скобках указывая переменные, от которых зависит предикат. Например, предикат«целое число x – четно» можно обозначить P(x). Этот предикат от одной переменной (одноместный предикат). Чтобы превратить его в высказывание, нужно придать значение переменной x. Предикат «x2 + y2 = 25» можно обозначить Q(x, y). Этот предикат от двух переменных (двуместный предикат). Чтобы превратить его в высказывание, необходимо уже придать конкретные значения паре переменных x, y. Понятно, что в предикат имеет смысл подставлять только те значения переменных, при которых он превращается в осмысленное предложение. Например, рассмотрим предикат «Он написал роман «Война и мир». Здесь роль переменной играет местоимение «он». Этот предикат превратиться в высказывание только в том случае, если мы вместо слова «он» будем подставлять фамилию и имя конкретного человека, а никак не число, не день недели и т.д. Отметим, что всякое уравнение и неравенство является предикатом. А решить уравнение или неравенство – значит найти все значения переменных, при которых этот предикат превращается в истинное высказывание. Определение. Предикат P называется тождественно истинным или тождеством, если он принимает истинные значения при всех значениях входящих в него переменных, при которых он становится высказыванием. Например, тождествами являются предикаты (x + y)2 = x2 + 2xy + y2 или sin2x + cos2 x = 1. Определение. Предикат P называется тождественно ложным или противоречием, если он принимает ложные значения при всех значениях входящих в него переменных, при которых он становится высказыванием. Например, тождествами являются предикаты x2 < 0 или sin(x y) = 2. По аналогии с высказываниями для всяких двух предикатов P и Q мы можем определить новые предикаты, полученные из P и Q при помощи логических связок отрицания, конъюнкции, дизъюнкции, импликации и эквиваленции. Таким же образом, как для высказываний, определяется равносильность предикатов. Логические операции преобразуют предикаты в новые предикаты. Рассмотрим теперь операции, преобразующие предикаты в высказывания. Одной из таких операций является подстановка вместо переменных их значений. Например, если в двуместном предикате «x делится на y» подставить вместо переменных x и y пару чисел 6 и 2, получим истинное высказывание «6 делится на 2», если подставить пару чисел 5 и 2, то получим ложное высказывание «5 делится на 2». Но существует и другой способ превращения предиката в высказывание. Рассмотрим два предложения: первое – «Всякое целое число x – четное», второе – «Существует четное число x». Это предложения с переменной, но подставлять сюда значения переменной не имеет смысла, они уже являются высказываниями, причем первое высказывание истинно, а второе ложно. В основе этих предложений лежит предикат P(x)– «целое число x – четное», но переменная x связана здесь словами «всякое» и «существует». Слова «всякий» и «существует» очень часто используются в математических предложениях, поэтому в математической логике они получили специальное название – кванторы. Термину «всякий» соответствует квантор всеобщности, обозначаемый " (перевернутая буква А, от английского слова All – все, всякий), термину «существует» соответствует квантор существования, обозначаемый $ (перевернутая буква E, от английского слова Exist – существует). Тогда логические формулы приведенных выше высказываний имеют вид "x P(x) и $x P(x). Переменная, к которой приписан квантор, называется связанной. Если мы рассматриваем предикат от нескольких переменных, то кванторы могут быть приписаны либо ко всем переменным, либо только к части переменных. Если все переменные связаны, то предикат становится высказыванием. Если связанной является только часть переменных, то оставшиеся переменные называются свободными, и мы имеем предикат от меньшего числа переменных. Например, рассмотрим предложение «для любого действительного числа x существует действительное число y, такое, что 2x + y = 5». Оно имеет логическую формулу "x $y Q(x, y), где Q(x, y) – предикат 2x + y = 5. Здесь обе переменные связаны, и это предложение является высказыванием. а предложение «существует действительное число y, такое, что 2x + y = 5» имеет логическую формулу $y Q(x, y). Здесь переменная y является связанной, а переменная x – свободной, значит, это предложение является предикатом от одной переменной x. Следует отметить очень важный факт: при рассмотрении высказываний с кванторами. полученных из предикатов от нескольких переменных, смысл высказываний существенно зависит от того, в каком порядке записаны кванторы и переменные, к которым они приписаны. Поясним это на примере. Пусть P(x, y) – это предикат «официант x обслуживает стол y». Составим из этого предиката различные высказывания с помощью кванторов: "x $y P(x, y) – «у любого официанта есть стол, который он обслуживает», "y $x P(x, y) – «для каждого стола есть официант, который его обслуживает», $y "x P(x, y) – «существует стол, который обслуживают все официанты», $x "y P(x, y) – «существует официант, который обслуживает все столы», "x "y P(x, y) – «каждый официант обслуживает все столы», "y "x P(x, y) – «каждый стол обслуживают все официанты», $x $y P(x, y) – «существует официант, который обслуживает некоторый стол», $y $x P(x, y) – «существует стол, обслуживаемый некоторым официантом». По смыслу приведенных высказываний видно, что только у двух последних пар высказываний, в которых переменные связаны одинаковыми кванторами, смысл одинаковый. Все остальные высказывания имеют различный смысл. Построим отрицание высказывания с кванторами. Рассмотрим в качестве примера высказывание «все рыбы умеют плавать». Это высказывание имеет логическую формулу "x P(x), где P(x) – предикат «рыба x умеет плавать». Тогда отрицанием исходного высказывания будет высказывание «неверно, что все рыбы плавают». Это высказывание означает, что существует рыба, которая не умеет плавать, то есть отрицание нашего высказывания имеет логическую формулу $x Рассмотрим высказывание «существует ядовитый гриб», оно имеет логическую формулу $x P(x), где P(x) – предикат «гриб x ядовитый». Отрицанием этого высказывания будет высказывание «неправда, что существует ядовитый гриб», или, что то же самое, «все грибы не являются ядовитыми». Это высказывание имеет логическую формулу "x Обобщим эти результаты на случай произвольного предиката. Для того, чтобы построить отрицание высказывания с квантором, нужно квантор всеобщности заменить на квантор существования (или наоборот), а предикат заменить его отрицанием. По такой же схеме строятся отрицания высказываний, содержащих несколько кванторов. Например, построим отрицание высказывания «В каждом городе Швеции есть улица, на которой находится дом, все окна которого выходят на юг». Этим отрицанием будет высказывание «В Швеции существует город, в котором на каждой улице во всех домах существует окно, не выходящее на юг». Задачи для самостоятельного решения 1.Какие из следующих выражений являются высказываниями, какие предикатами? Для высказываний определите их значение истинности. 1) Солнце вращается вокруг Земли. 2) В романе Толстого «Война и мир» 14563970 слов. 3) Да здравствует солнце, да скроется тьма! 4) Студент 1 курса. 5) sin2x + cos2 x = 1. 6) Число 3 удовлетворяет неравенству 3x + 25 £ 0. 7) Натуральное число x больше 8. 2.Определите значение истинности следующих высказываний. 1) (2 ´ 3 ³ 6) Ú (3 ´ 3 > 7). 2) (23 > 7) Ù (2 > 7). 3) Если 12 делится на 6, то 12 делится на 3. 4) Если 15 делится на 6, то 15 делится на 3. 5) 15 делится на 6 тогда и только тогда, когда 15 делится на 3. 6) 12 делится на 6 тогда и только тогда, когда 12 делится на 3. 7) Неверно, что 12 < 32. 8) (2 ´ 3 ³ 6) Ú 9) 10) ((22 < 4) Ú (7 > 5)) ® 11) 3.Среди следующих пар высказываний выберите те, которые являются отрицаниями друг друга. 1) 5 < 2 и 5 > 2. 2) 5 £ 2 и 5 ³ 2. 3) 5 < 2 и 5 ³ 2. 4) «Число 3 положительно» и «число 3 отрицательно». 5) «Число 3 четно» и «число 3 нечетно». 6) «Вечером я пойду в кино» и «вечером я пойду в театр». 4.Определите значение истинности высказывания А, если следующие высказывания истинны: 1) A Ù (2 ´ 2 £ 5), 2) A Ú (3 ´ 3 > 7), 3) Если A, то 4 – нечетное число, 4) A тогда и только тогда, когда 22 = 5. 5.Определите значение истинности высказывания А, если следующие высказывания ложны: 1) A Ù (2 ´ 2 £ 4), 2) A Ú (2 ´ 2 ³ 5), 3) Если 2 –четное число, то A, 4) Если A, то 4 – нечетное число, 5) A тогда и только тогда, когда 22 = 4, 6) 6.Следующие высказывания расчлените на простые высказывания, обозначьте их буквами и запишите в виде логической формулы. 1) «Если мистер Джонс счастлив, то миссис Джонс несчастлива, и если мистер Джонс несчастлив, то миссии Джонс счастлива». 2) «Если ни в Варшаву мы не поедем, ни в горы мы не отправимся, то мы ежедневно будем ходить на пляж или, если будет дождь, будем читать дома книги». 3) «Если «Спартак» и «Динамо» проиграют, а «ЦСКА» выиграет, то «Зенит» потеряет первое место, и на третье место выйдет «Рубин». 7.Пусть P означает «сегодня идет дождь», Q – «сегодня ясно», R – «сегодня идет снег», S – «вчера было пасмурно». Расшифруйте: 1) 2) 3) 4) 8.Запишите отрицание следующего высказывания, не используя слова «неверно, что»: «Если летом будет дождливая погода, то ни накупаться, ни загореть нам не удастся». Проанализируйте предложенный ниже способ решения, выделите отдельные этапы. Решение:Обозначим высказывания: A – «летом будет дождливая погода», B – «нам удастся накупаться», C – «нам удастся загореть». Тогда исходное высказывание имеет формулу:
Эта формула соответствует высказыванию «Летом будет дождливая погода и нам удастся накупаться или загореть». 9.Сформулируйте отрицания следующих высказываний в утвердительной форме, то есть так, чтобы они не начинались со слов «неверно, что»: 1) Если я поздно приду на остановку и не смогу сесть в автобус, то опоздаю на занятия и пропущу интересную лекцию. 2) Если завтра будет воскресенье или в институте не будет занятий, то ко мне придут друзья, и мы послушаем музыку. 3) После обеда я отправлюсь на прогулку в парк или, если ко мне зайдет приятель, буду играть с ним в шахматы или мы посмотрим кино. 10.С помощью таблиц истинности докажите законы логики высказываний, приведенные выше. 11.Разберитесь в предложенном доказательстве равносильности формул. Около каждой стрелки «Û» укажите номер закона, который применен:
Доказательство:
12.Докажите равносильность следующих формул: 1) 2) 3) 4) 5) 13.Упростите следующие формулы, то есть замените их на равносильные формулы более простого вида: 1) 2) 3) 14.Родители сказали детям: «Если мы поедем летом в дом отдыха, то вы поедете в лагерь». В школе детей спросили, куда они поедут летом. Петя ответил: «Если мы поедем в лагерь, то родители поедут в дом отдыха». Галя сказала: «Если папа с мамой не поедут в дом отдыха, то мы не поедем в лагерь». «Нет, не так», – вмешался Коля, – «Если мы не поедем в лагерь, то родители не поедут в дом отдыха». Чей ответ равносилен тому, что сказали родители? 15.Решите задачу: На вопрос: «Кто из трех студентов изучал логику?» – был получен верный ответ: «Если изучал первый, то изучал и третий, но неверно, что если изучал второй, то изучал и третий». Кто изучал логику? Проверьте свой ответ, проанализировав предложенный способ решения. Решение.Обозначим высказывания: a – «Первый студент изучал логику», B – «Второй студент изучал логику», c – «Третий студент изучал логику». Составим формулу, которая соответствует ответу на вопрос и которая по условию должна быть истинной:
Так как конъюнкция истинна только в случае одновременной истинности всех своих членов, то получаем, что высказывание А ложно, B – истинно, С – ложно. Ответ: Второй студент изучал логику, а первый и третий не изучали. 16.Определите, кто из четырех студентов сдал экзамен, если известно, что выполнены следующие условия: 1) Если первый сдал, то и второй сдал. 2) Если второй сдал, то третий сдал или первый не сдал. 3) Если четвертый не сдал, то первый сдал, а третий не сдал. 4) Если четвертый сдал, то и первый сдал. 17.Запишите следующие высказывания в виде формул с кванторами, предварительно введя обозначения для используемых предикатов: 1) Некоторые реки впадают в Каспийское море. 2) Все люди знают, что Земля круглая. 3) По крайнее мере, одно целое число делится на 8. 4) Не все птицы умеют летать. 5) Ни одна собака не умеет мяукать. 6) Кто хочет, тот добьется. 18.Рассмотрим предикат x < 3 + y. С помощью кванторов получите из него различные высказывания. Определите, какие из полученных высказываний является истинными, какие – ложными. 19.Среди следующих предложений найдите пары высказываний, являющиеся отрицаниями друг друга. 1) Все ученики нашего класса решили задачу. 2) Некоторые ученики нашего класса решили задачу. 3) Ни один ученик нашего класса не решил задачу3. 4) Некоторые ученики нашего класса не решили задачу. 20.Сформулируйте отрицания следующих высказываний, не употребляя слова «неверно, что»: 1) Весь наш класс присутствовал на творческом вечере. 2) Некоторым школьникам по 10 лет. 3) В некотором поезде, идущем из Саратова в Воронеж, в каждом вагоне есть свободное место. 4) В каждом городе есть район, в каждой школе которого найдется класс, ни один ученик которого не занимается спортом. 5) Найдется книга, содержащая страницу, в каждой строке которой встречается хотя бы одна буква «А». 
12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 Ú B ® C Ù B.
Ú B ® C Ù B. является противоречием.
является противоречием. – закон двойного отрицания.
– закон двойного отрицания. – коммутативность конъюнкции.
– коммутативность конъюнкции.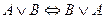 – коммутативность дизъюнкции.
– коммутативность дизъюнкции. – ассоциативность конъюнкции.
– ассоциативность конъюнкции. – ассоциативность дизъюнкции.
– ассоциативность дизъюнкции. ,
, – законы де Моргана.
– законы де Моргана. ,
, – законы дистрибутивности.
– законы дистрибутивности. .
.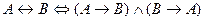 .
. ,
, – законы поглощения.
– законы поглощения. ,
, – законы идемпотентности.
– законы идемпотентности. .
.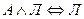 .
.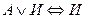 .
. .
. .
. .
. .
. .
.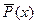 , где
, где 

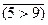 .
.
 ,
,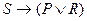 ,
, ,
, .
. . Составим его отрицание и упростим его:
. Составим его отрицание и упростим его: .
. .
.

 ,
,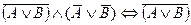 ,
,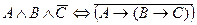 ,
, ,
,
 ,
,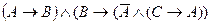 ,
, .
. . Упростим эту формулу.
. Упростим эту формулу. .
.