Виброакустические сигналы и их описание

Если в среде распространяется виброакустический сигнал, то фронтом волны является граница между возмущенной и невозмущенной областями среды. Такая граница во многих случаях является условной, так как в упругой волне возмущение нарастает постепенно и самое начало упругого возмущения может быть просто не зарегистрировано аппаратурой ввиду его малости. Часто за положение фронта принимают поверхность, соответствующую уровню звукового давления в 10 %от максимального. Различают передний и задний фронт импульса. Длительность переднего фронта - время нарастания сигнала от 10 до 90% его максимального значения, заднего - время спада с 90 до 10%. Кроме того, виброакустический импульс уже не является гармонической волной: он не может быть описан гармонической функцией. Но он может быть описан совокупностью таких функций.

Заметим, однако, что указанный импульс описывается функцией, близкой гармонической: он является синусоидой с определенной частотой, часто называемой частотой заполнения или несущей частотой (по аналогии с радиотехникой), но амплитуда этой синусоиды является переменной. Изменение амплитуды задается функцией (модулирующей функцией), изменяющейся медленно по сравнению с заполняющей синусоидой:

s(t) = A(t)sinW_ot, (1.1)

где А(t)-модулирующая функция времени, w_o=2πt_o - круговая частота возбуждаемых колебаний, f_o- частота колебаний.

Математическую основу частотного описания сигналов дает аппарат преобразования Фурье. По физической сути преобразования Фурье отражают возможность двойственного описания любой изменяющейся во времени физической величины (сигнала), а именно во временной или в частотной области. Изменения величины во времени можно наблюдать на экране осциллографа, на диаграмме самописца. Но, то же самое изменение можно записать на магнитную ленту и прослушать через наушники, получив частотное представление о сигнале. Природа наградила человека очень точным и чувствительным Фурье-анализатором: слуховым аппаратом, содержащим около тридцати тысяч частотных фильтров. На слух мы воспринимаем изменяющийся со временем Фурье-образ обычного акустического сигнала, отсюда следует важный вывод о том, что при создании контрольно- измерительной диагностической аппаратуры выбор того или иного (временного или частотного) представление сигнала определяется удобством его анализа при решении конкретных задач.

Если сигнал во временной области описывается функцией S(t), то его частотное представление S(ω) в общем случае может быть получено с помощью прямого преобразования Фурье:

S(ω) = ∫ s (t) exp (-iωt)dt (1.2)

В приведенной (1.2) и последующих формулах i – мнимая единица, ω – циклическая частота. Поскольку ехр(-iωt) = cos ωt- i sin ωt есть комплексная функция, S(ω) тоже является комплексной и характеризуется действительной Re(S) и мнимой Im(S) составляющими:

Re (S) = ∫ s(t) cos ωt dt; (1.3)

Im (S) = ∫ s(t) sin ωt dt (1.4)

в соответствии со свойствами комплексных чисел:

|S| = √(ReS)² +(ImS)² (1.5)

модуль спектра, равный амплитуде колебаний, соответствующей гармонической составляющей сигнала;

φ =arctg (ImS/ReS) (1.6)

- фаза гармонической составляющей

Обратное преобразование Фурье позволяет восстановить сигнал S(t) по его известному спектральному представлению (образу):

S(t) = 1 /2π ∫ S(ω)exp (ωt) dω (1.7)

если сигнал s{t} периодический и имеет период Т, вместо интеграла, получим ряд Фурье

S(t) = ∑ S_nexp (iω_nt) (1.8)

В этом случае коэффициенты Фурье Sn (амплитуды соответствующих гармонических составляющих сигнала) вычисляют по формуле

Sn = 1/T ∫ S(t) exp (-ω_nt) dt (1.9)

причем w_n=2πn/T= 2π f_n - частота повторения сигналов. В связи с изложенным сделаем несколько полезных выводов.

Во-первых, отрицательных частот в природе не существует, так же как и комплексных физических величин, поэтому применение соответствующих понятий есть одна лишь удобная для математических вычислений форма записи. Например, в представленной форме очень удобно дифференцировать и интегрировать выражения: образ Фурье от производной сигнала получается простым умножением образа самого сигнала на -iω, а от интеграла - делением на ту же величину, причем дифференцирование и интегрирование подобным образом могут заменяться сколько угодно раз. Учет реально отсутствующих отрицательных частот производится их отбрасыванием в конечном результате расчетов и удвоением амплитуд реально существующих компонент с положительными частотами.

Во-вторых, разложение в ряд Фурье есть представление сигнала бесконечной суммой синусоид, имеющих частоты, кратные основной частоте. Синусоида с бесконечной частотой не существует, равно как и сигнал с бесконечно быстро нарастающим фронтом.

Поэтому количество членов в ряде Фурье (или пределы интегрирования в интеграле Фурье) связано с реальным временем нарастания сигнала - длительностью его переднего фронта. Эта величина должна быть сопоставима со временем нарастания синусоиды с наибольшим номером и соответственно с наиболее высокой частотой. Время нарастания синусоиды от нуля до максимального значения равно четверти ее периода, т.е. ¼ n f_n. Недостаток высокочастотных составляющих характеризуется затягиванием нарастания и спада сигнала, появлением в нем " хвостов".

Медленные изменения сигнала, наоборот, отражаются синусоидами с малыми частотами, недостаток которых приводит к чрезмерно быстрому изменению вершины сигнала. Влияние соответствующих частотных ограничений сигнала на его искажения иллюстрирует рис.1.1.

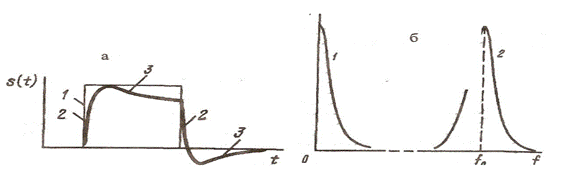
Рис. 1. 2. а. Характер искажений импульсного сигнала при ограничении его частотного спектра 1 - исходный импульс; 2 - искажения из-за ограничения высокочастотных составляющих сигнала; 3 - искажения из - за ограничения низкочастотных составляющих; б. Перенос спектра при детектировании квазигармонического сигнала 1 — после детектирования; 2 - исходный спектр.

Обратимся к случаю, характерному для практики акустического контроля, когда акустический сигнал возникает:

- в результате возбуждения собственных колебаний объекта, например при работе насоса;

- на приемнике системы ультразвукового контроля;

- при регистрации сигналов акустической эмиссии.

Сходство этих трех случаев состоит в том, что регистрируемый сигнал представляет собой квазигармонический (почти гармонический) сигнал или совокупность таких сигналов, несущие частоты которых равны собственным частотам объекта или приемника, или того и другого вместе.

Для квазигармонических сигналов существует простое правило определения их спектра по спектру модулирующей функции: спектр модулирующей функции переносится по оси частот на величину, равную значению модулирующей частоты. В результате спектр оказывается сгущенным около несущей частоты. Рассмотрим характерный для акустического контроля пример, когда модулирующая функция имеет вид

S(t) = A₀e ^–βt (1.10)

т. е. сигнал имеет вид:

S(t) = A₀e ^–βt sinβω₀t (1.11)

Расчет показывает, что спектр Фурье модулирующей функции дается выражением

S_A(ω) = A₀/(β+iω) (1.12)

|S_A(ω)| = A₀/ √(β² +ω²) (1.13)

а модуль этой функции для соответствующей модулированной функции

S(ω) = ω₀

(ω₀²– ω²) + 2iβω+ β² (1.14)

| S(ω) | = ω₀

√(ω₀²– ω²)² + 2β²ω² (1.15)

Модуль спектра достигает максимума на частотах ±ω0 (рис. 1.1б), а соответствующая ему функция имеет вид резонансной кривой с шириной.

Δω=ω₀/Q = β√2 (1.16)

Одно из важных следствий переноса спектра состоит в том, что вместо обработки высокочастотного сигнала, требующей высокой частоты дискретизации, можно ограничиться частотой дискретизации, равной удвоенной максимальной частоте спектра модулирующей функции. Сказанное отражает тот факт, что высокочастотный квазигармонический сигнал содержит гораздо меньше информации, чем это может показаться на первый взгляд. Обращают на это особое внимание в связи с тем, что недемпфированные или слабо демпфированные пьезопреобразователи при импульсном электрическом или механическом воздействии на них вырабатывают сигнал в виде суммы

S(t) = ∑ A _0ie –β^it sin (ω_0it) (1.17)

в которой ω_{oi –} I собственная частота соответствующая той или иной форме колебаний, β_oi - коэффициент затухания собственных колебаний на этой частоте.

Не нашли, что искали? Воспользуйтесь поиском по сайту: