
|
|
В14. Мода и медиана непрерывной случайной величины.12 Мода ( Медианой (
.
В15. Биномиальный закон распределения и его числовые характеристики. Биномиальное распределение описывает повторяющиеся независимые опыты. Этот закон определяет появление события
где:
В15. Равномерный закон распределения, графики функции и плотности распределения, числовые характеристики. Непрерывная случайная величина считается равномерно распределенной, если ее плотность вероятности имеет вид:
Математическое ожидание случайной величины, имеющей равномерное распределение:
Дисперсия может быть вычислена следующим образом:
Среднее квадратичное отклонение будет иметь вид:
В17. Показательный закон распределения, графики функции и плотности распределения, числовые характеристики. Показательным распределением непрерывной случайной величины
где Функция распределения вероятности в этом случае имеет вид:
Математическое ожидание случайной величины, имеющей экспоненциальное распределение, получаем на основании общей формулы с учетом того, что
Интегрируя это выражение по частям, находим: Дисперсию для экспоненциального распределения можно получить, используя выражение:
Подставляя выражение для плотности вероятности, находим:
Вычисляя интеграл по частям, получаем:
В16. Нормальный закон распределения, графики функции и плотности распределения. Стандартное нормальное распределение. Функция отраженного нормального распределения. Нормальным называется такое распределение случайной величины
где
График плотности нормального распределения называют нормальной кривой Гаусса.
В18. Неравенство Маркова. Обобщенное неравенство Чебышева. Если для случайной величины X существует Оно вытекает из обобщенного неравенства Чебышева: Пусть функция
В19. Закон больших чисел в форме Чебышева. Его смысл. Следствие закона больших чисел в форме Чебышева. Закон больших чисел в форме Бернулли. Под законом больших чисел в теории вероятностей понимается ряд теорем, в каждой из которых устанавливается факт асимптотического приближения среднего значения большого числа опытных данных к математическому ожиданию случайной величины. В основе доказательств этих теорем лежит неравенство Чебышева. Это неравенство можно получить, рассматривая дискретную случайную величину, имеющую Теорема. Пусть имеется конечная последовательность
Тогда, каково бы ни было число
стремится к единице при Теорема Чебышева устанавливает связь между теорией вероятностей, которая рассматривает средние характеристики всего множества значений случайной величины, и математической статистикой, оперирующей ограниченным множеством значений этой величины. Она показывает, что при достаточно большом числе измерений некоторой случайной величины среднее арифметическое значений этих измерений приближается к математическому ожиданию.
В20. Предмет и задачи математической статистики. Генеральная и выборочная совокупности. Способ отбора. Математическая статистика – наука о математических методах систематизации и использования статистических данных для научных и практических выводов, опирающаяся на теорию вероятностей. Объектами изучения математической статистики являются случайные события, величины и функции, которые характеризуют рассматриваемое случайное явление. Случайными являются следующие события: выигрыш на один билет денежной лотереи, соответствие контролируемого продукта установленным требованиям, безотказная работа автомобиля в течение первого месяца его эксплуатации, выполнение подрядчиком суточного графика работ. Выборочной совокупностью называют совокупность случайно отобранных объектов. Генеральной совокупностью называют совокупность объектов, из которых производится выборка. В21. Способы отбора. Способы отбора: 1 Отбор, не требующий расчленения генеральной совокупности на части. Сюда относятся а) простой случайный бесповторный отбор и б) простой случайный повторный отбор. 2) Отбор, при котором генеральная совокупность разбивается на части. Сюда относятся а) типический отбор, б) механический отбор и в) серийный отбор. Простым случайным называют отбор, при котором объекты извлекаются по одному из генеральной совокупности. Типическим называют отбор, при котором объекты отбираются не из всей генеральной совокупности, а из каждой ее «типической» части. Механическим называют отбор, при котором генеральная совокупность механически делится на столько групп, сколько объектов должно войти в выборку, а из каждой группы выбирается один объект. Серийным называют отбор, при котором объекты отбирают из генеральной совокупности не по одному, а «сериями», которые подвергаются сплошному обследованию.
В22. Статистический и вариационный ряд. Эмпирическая функция распределения и ее свойства. Вариационный ряд для дискретных и непрерывных случайных величин. Пусть из генеральной совокупности извлечена выборка, причем значение исследуемого параметра
Статистическим распределением выборкиназывают перечень вариант и соответствующих им относительных частот. Статистическое распределение можно представить как:
где относительные частоты Эмпирической функцией распределения называют функцию Свойства эмпирической функции распределения: 1) Значения эмпирической функции принадлежат отрезку [0,1]. 2) Эмпирическая функция распределения выборки служит для оценки теоретической функции распределения генеральной совокупности.
В23,24,25. Числовые характеристики выборки (Выборочные средняя дисперсия, исправленная дисперсия, среднеквадратическое отклонение, моменты). Для охарактеризования рассеяния наблюдаемых значений количественного признака выборки вокруг среднего значения
Если значения признака
Выборочное среднее является несмещенной состоятельной оценкой генерального среднего. В то же время, несмещенной состоятельной оценкой генеральной дисперсии оказывается не выборочная дисперсия
В29. Основные понятия статистической проверки гипотез. Основная и конкурирующая гипотезы, критерий проверки, ошибки первого и второго рода. Статистической называют гипотезу о виде неизвестного распределения или о параметрах известных распределений. Примеры статистических гипотез: генеральная совокупность распределена по закону Пуассона; дисперсии двух нормальных распределений равны между собой. Наряду с выдвинутой гипотезой рассматривают и противоречащую ей гипотезу. Если выдвинутая гипотеза будет отвергнута, то имеет место противоречащая гипотеза. Нулевой (основной)называют выдвинутую гипотезу Альтернативной (конкурирующей)называют гипотезу Ошибка первого родасостоит в том, что будет отвергнута правильная гипотеза.Следует отметить, что последствия ошибок могут оказаться различными. 
12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 ) непрерывной случайной величины
) непрерывной случайной величины  – это такое ее значение, которому соответствует максимальное значение ее плотности вероятности.
– это такое ее значение, которому соответствует максимальное значение ее плотности вероятности. ) непрерывной случайной величины
) непрерывной случайной величины  .
. раз при
раз при  независимых испытаниях, если вероятность появления события в каждом из этих
независимых испытаниях, если вероятность появления события в каждом из этих  не изменяется от опыта к опыту. Вероятность:
не изменяется от опыта к опыту. Вероятность: ,
,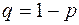 – вероятность непоявления события в опыте;
– вероятность непоявления события в опыте; – заданное число появления события в
– заданное число появления события в  – число сочетаний из
– число сочетаний из 
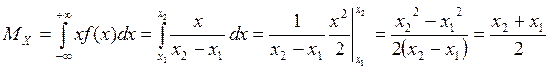


 .
. ,
, – постоянная положительная величина.
– постоянная положительная величина.
 при
при  :
: .
. .
. .
.
 .
.
 – среднее квадратичное отклонение;
– среднее квадратичное отклонение; – математическое ожидание случайной величины.
– математическое ожидание случайной величины.
 , то для любого
, то для любого  справедливо неравенство Маркова
справедливо неравенство Маркова  .
. монотонно возрастает и неотрицательна на
монотонно возрастает и неотрицательна на  . Если для случайной величины X существует
. Если для случайной величины X существует  , то для любого
, то для любого  .
. возможных значений
возможных значений  .
. независимых случайных величин, с одним и тем же математическим ожиданием
независимых случайных величин, с одним и тем же математическим ожиданием  и дисперсиями, ограниченными одной и той же постоянной
и дисперсиями, ограниченными одной и той же постоянной  :
:
 .
. , вероятность события
, вероятность события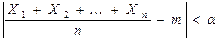
 .
. наблюдалось
наблюдалось  раз,
раз,  -
-  раз и т.д. При этом
раз и т.д. При этом  объем выборки. Наблюдаемые значения
объем выборки. Наблюдаемые значения  называют вариантами, а последовательность вариант, записанных в возрастающем порядке – вариационным рядом. Числа наблюдений называют частотами,а их отношения к объему выборки
называют вариантами, а последовательность вариант, записанных в возрастающем порядке – вариационным рядом. Числа наблюдений называют частотами,а их отношения к объему выборки  -относительными частотами. Вариационный рядможно представить таблицей вида:
-относительными частотами. Вариационный рядможно представить таблицей вида:

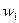


 .
. , определяющую для каждого значения x относительную частоту события X<x. Таким образом, по определению
, определяющую для каждого значения x относительную частоту события X<x. Таким образом, по определению  , где
, где  – число вариант, меньших x, n – объем выборки.
– число вариант, меньших x, n – объем выборки. , если
, если  – наибольшая варианта, то
– наибольшая варианта, то  .
. вводится выборочная дисперсия. Выборочной дисперсией
вводится выборочная дисперсия. Выборочной дисперсией 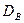 называют среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения
называют среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения  признака выборки объема n различны, то:
признака выборки объема n различны, то: .
. имеют частоты
имеют частоты  соответственно, причем
соответственно, причем 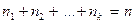 , то:
, то: .
. .
. .
. , которая противоречит нулевой. Например, если нулевая гипотеза состоит в предположении, что математическое ожидание нормального распределения равно 5, то альтернативная гипотеза, например, может состоять в предположении, что
, которая противоречит нулевой. Например, если нулевая гипотеза состоит в предположении, что математическое ожидание нормального распределения равно 5, то альтернативная гипотеза, например, может состоять в предположении, что  . Кратко это записывают так:
. Кратко это записывают так:  .
.