
|
|
Этапы проведения анализа связи переменных.Задача № 1. Длина первого молярного X и второго молярного Y зубов у ископаемого Phenacodus primaevus оказались следующими:
Определите величину коэффициента корреляции и оцените его значимость. В случае выявления корреляционной связи, представить графически поле корреляции признаков.
Теория: Корреляционный анализ – это анализ, с помощью которого возможно выявление причинно-следственной связи между факторными и результативными признаками (при оценке физического развития, для определения связи между условиями труда, быта и состоянием здоровья, при определении зависимости частоты случаев болезни от возраста, стажа, наличия производственных вредностей и др.), а также – выявление зависимости параллельных изменений нескольких признаков от какой-то третьей величины. Этапы проведения анализа связи переменных. 1.Корреляционный анализ. Корреляционный анализ дает информацию о характере и степени выраженности связи (по величине коэффициента корреляции), которая используется для отбора существенных факторов, а также для расчета параметров регрессионных уравнений. 2. Расчет параметров и построение регрессионных моделей. Здесь стремятся отыскать наиболее точную меру выявленной связи, для того чтобы можно было прогнозировать, предсказывать значения зависимой величины Y, если будут известны значения независимых величин X1, Х2, .... Хп. 3. Выяснение статистической значимость, т.е. пригодности постулируемой модели для использования ее в целях предсказания значений. 4. Применение статистически значимой модели для прогнозирования (предсказания), управления или объяснения. Если же обнаружена незначимость, то модель отвергают, предполагая, что истинной окажется какая-то другая форма связи, которую надо поискать. Коэффициент корреляции одним числом измеряет силу связи между изучаемыми явлениями и дает представление о ее направленности. По направлению связь может быть прямой или обратной. По силе связи коэффициенты корреляции колеблются от 1 (полная связь) до 0 (отсутствие связи). Коэффициент корреляции может иметь значение от –1 до +1, т.е. иметь отрицательное либо положительное значение. В этих случаях говорят об обратной или прямой корреляционной взаимосвязи. Решение:
В начале проводим анализ данных предложенных в таблице. Данные относятся к количественным признакам. В статистическом анализе используют 3 типа медико-биологических данных: количественные, качественные и порядковые. Количественные данные бывают: непрерывные (масса тела, температура, уровень сахара в крови) и дискретные (число рецидивов за период, количество перенесенных операций). Вносим данные в программу Medstat→Новые данные→Вариационный ряд.
Вариация признака (или фактора, или результатов измерения) возникает, если их значения меняются от индивидуума к индивидууму или для одного индивидуума во времени. Едва ли не всем характеристикам организма человека, будь то физиологические, биохимические или иммунологические, свойственна вариабельность. Вариационный ряд – это совокупность изменяющихся значений какого-либо признака, фактора, результата измерения. Вводим данные в таблицу.
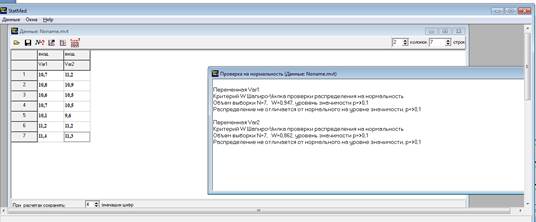
Проверяем на нормальность.
Получаем, что обе выборки не отличаются от нормальных:
Переменная Var1 Критерий W Шапиро-Уилка проверки распределения на нормальность Объем выборки N=7, W=0,947, уровень значимости p=>0,1 Распределение не отличается от нормального на уровне значимости, p=>0,1
Переменная Var2 Критерий W Шапиро-Уилка проверки распределения на нормальность Объем выборки N=7, W=0,862, уровень значимости p=>0,1 Распределение не отличается от нормального на уровне значимости, p=>0,1
Так как распределение не отличаются от нормального, то для вычисления коэффициента корреляции используем коэффициент корреляции Пирсона. Коэффициент корреляции Пирсона рассчитывается по формуле:
где X и Y – варианты сопоставляемых вариационных рядов, dx и dy – отклонение каждой варианты от своей средней арифметической (Mx и My). Проверка значимости линейной корреляционной связи для двух выборок.
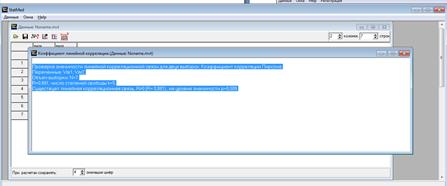
Получим: Проверка значимости линейной корреляционной связи для двух выборок. Коэффициент корреляции Пирсона. Переменные: Var1, Var2. Объем выборки: N=7. R=0,881, число степеней свободы k=5. Существует линейная корреляционная связь, R>0 (R= 0,881) , на уровне значимости p=0,009.
Коэффициент корреляции может иметь значение от –1 до +1, т.е. иметь отрицательное либо положительное значение. В этих случаях говорят об обратной или прямой корреляционной взаимосвязи. Величина коэффициента характеризует силу корреляционной взаимосвязи. Чем ближе модуль коэффициента корреляции к единице, тем сильнее или глубже корреляционная взаимосвязь между двумя вариационными рядами. Модульное значение выше 0,8 характеризуют сильную взаимосвязь, в интервале 0,8-0,5 – выраженную взаимосвязь, 0,5-0,2 – слабую взаимосвязь, менее 0,2 (0,2 – 0) – отсутствие взаимосвязи. Представим в графическом виде:
Задача № 2. В статистике, как и в жизни, важные утверждения редко удается доказать окончательно и неоспоримо. Можно только выдвинуть утверждение, справедливое с некоторой степенью достоверности. Такое утверждение называют статистической гипотезой. Наиболее частыми задачами медицинских и биологических исследований, для решения которых оказывается необходимым сформулировать статистические гипотезы, являются следующие: - анализ соответствия распределения значений признака в изучаемой группе какому-либо определенному закону (например, анализ соответствия нормальному закону) - сравнение групп по параметрам распределений признака (например, по средним значениям, дисперсиям). Для решения любой подобной задачи формулируются две статистические гипотезы: 1. Нулевая гипотеза Н0 – предположение, что разница между генеральными параметрами сравниваемых групп равна нулю и различия, наблюдаемые между выборочными характеристиками, носят исключительно случайный характер; 2. Альтернативная гипотеза Н1 – противоположная нулевой –гипотеза о существовании различий между генеральными параметрами сравниваемых групп. Обычно статистическая гипотеза формулируется таким образом, что бы она была противоположна той исследовательской (медицинской, биологической) гипотезе, которая послужила поводом для проведения исследования. Например, необходимо проверить эффективность применения препарата. Пусть есть две группы испытуемых. Одна принимает препарат, а вторая нет. Тогда в качестве нулевой гипотезы Н0 можно принять гипотезу об отсутствии различия между результатами первой и второй группы. Тогда альтернативная гипотеза Н1- наличие различий между группами. Ошибка первого рода иначе называется уровнем статистической значимости. Уровень значимости - это максимально приемлемая для исследователя вероятность ошибочно отклонить нулевую гипотезу, когда она на самом деле верная, т.е. допускаемая исследователем величина ошибки первого рода. Величина уровня значимости устанавливается исследователем произвольно, однако обычно принимается равным 0,05, 0,01 или 0,001.
Решение: Для решения задачи используем программу Medstat. Данные имеют количественные признаки. В статистическом анализе используют 3 типа медико-биологических данных: количественные, качественные и порядковые. Количественные данные бывают: непрерывные (масса тела, температура, уровень сахара в крови) и дискретные (число рецидивов за период, количество перенесенных операций). Выбираем вкладку Medstat→Новые данные→Вариационный ряд. Вариационный ряд – это совокупность изменяющихся значений какого-либо признака, фактора, результата измерения.
Так как нам даны группы больных с острым, подострым и хроническим течением болезни. Для каждой группы проводим проверку на нормальность. Проводим проверку на нормальность для группы с острым течением.
Критерий Шапиро-Уилка используется для проверки гипотезы: «случайная величина распределена нормально» и является одним наиболее эффективных критериев проверки нормальности. Критерии, проверяющие нормальность выборки, являются частным случаем критериев согласия. Базируется на анализе линейной комбинации разностей порядковых статистик. Если выборка нормальна, можно далее применять мощные параметрические критерии. Проверяем на нормальность 2 группу больных с подострым течением болезни. Переменная Var1 Критерий W Шапиро-Уилка проверки распределения на нормальность Объем выборки N=13, W=0,965, уровень значимости p=>0,1 Распределение не отличается от нормального на уровне значимости, p=>0,1 Переменная Var2 Критерий W Шапиро-Уилка проверки распределения на нормальность Объем выборки N=13, W=0,954, уровень значимости p=>0,1 Распределение не отличается от нормального на уровне значимости, p=>0,1 Теперь проверяем на нормальность 2 группу больных с подострым течением болезни. Переменная Var1. Критерий W Шапиро-Уилка проверки распределения на нормальность Объем выборки N=11, W=0,956, уровень значимости p=>0,1 Распределение не отличается от нормального на уровне значимости, p=>0,1. Переменная Var2. Критерий W Шапиро-Уилка проверки распределения на нормальность Объем выборки N=11, W=0,939, уровень значимости p=>0,1 Распределение не отличается от нормального на уровне значимости, p=>0,1. Проводим проверки на нормальность для больных с хроническим течением. Переменная Var1 Критерий W Шапиро-Уилка проверки распределения на нормальность Объем выборки N=14, W=0,940, уровень значимости p=>0,1 Распределение не отличается от нормального на уровне значимости, p=>0,1 Переменная Var2 Критерий W Шапиро-Уилка проверки распределения на нормальность Объем выборки N=14, W=0,939, уровень значимости p=>0,1 Распределение не отличается от нормального на уровне значимости, p=>0,1 Так как распределение не отличается от нормального используем нормальный закон распределения. Выбираем вкладку описательная статистика. Закон распределения случайной величины - это отношение, устанавливающее связь между возможными значениями случайной величины и вероятностями, с которыми принимаются эти значения. Закон распределения полностью характеризует случайную величину. При построении математической модели для проверки статистической гипотезы необходимо ввести математическое предположение о законе распределения СВ (параметрический путь построения модели). Нормальное (гауссово) распределение.Одним из самых важных распределений в статистике является нормальное распределение. Непрерывная случайная величина Х называется распределенной по нормальному закону, если ее плотность распределения равна:
где m - математическое ожидание случайной величины; Функция плотности нормального распределения вероятности симметрична относительно среднего Свойства функции плотности нормального распределения вероятности: • полностью определяется двумя параметрами – средним ( • колоколообразная (унимодальная) форма; • симметричная относительно среднего; • сдвигается вправо, если среднее увеличивается, и влево, если среднее уменьшается (при постоянной дисперсии); • сплющивается, если дисперсия увеличивается, но становится более остроконечной, если дисперсия уменьшается (для постоянного среднего). • среднее и медиана нормального распределения равны. Нормальное распределение не является единственным известным распределением. Среднее арифметическое получают путем сложения всех значений и деления этой суммы на число значений в наборе. Набор n наблюдений переменной x можно изобразить как
Стандартное отклонение.Стандартное (среднеквадратичное) отклонение ( На практике часто приходится сравнивать изменчивость признаков, выраженных разными единицами, например, рост в см и масса в кг. Если разделить стандартное отклонение на среднее арифметическое и выразить результат в процентах, получится коэффициент вариации. Он является мерой рассеяния, не зависящей от единиц измерения (безразмерной).
При Доверительный интервал.Выборка из популяции позволяет получить точечную оценку интересующего нас параметра и вычислить стандартную ошибку для того, чтобы указать точность оценки. Следует отметить, что для большинства исследований стандартная ошибка как таковая неприемлема, поскольку она, в отличие от стандартного отклонения, не отражает вариабельности в значениях данных. Гораздо полезнее объединить эту меру точности синтервальной оценкой для параметра популяции. Для этого нужно вычислитьдоверительный интервал (ДИ), который дает вероятное значение верхней и нижней границ оцениваемой неизвестной величины, что позволяет заявить: «Я утверждаю, что точное значение неизвестной величины с определённой вероятностью (чаще всего эта вероятность составляет 0,95) находится между этими двумя числами». Обычно доверительные интервалы показывают, насколько надежной в действительности является статистическая оценка. Доверительный интервал для среднего в случае нормального распределения. Доверительные интервалы представляют оценку в некоторой перспективе и позволяют избежать необходимости указывать одно и то же число как точное значение, в то время как фактически в биологии это число точным никогда и не является. При интерпретации ДИ исследователь формулирует следующие вопросы: Широкий ДИ указывает на менее точную оценку, узкий - на более точную оценку.
Верхние и нижние пределы показывают, будут ли результаты клинически (биологически) значимы. Можно проверить, попадает ли вероятное значение для параметра популяции в пределыДИ. Если да, то результаты согласуются с этим вероятным значением. Если нет, то маловероятно (для 95%ДИшанс меньше 5%), что параметр имеет это значение.
Так как распределение не отличается от нормального для расчета используем вкладку Сравнение для 2 связанных выборок в программе Medstat. Стандартная, но существеннейшая статистическая задача – сравнение значений переменной (или нескольких однотипных переменных) в нескольких группах (или подгруппах), выбранных из генеральной совокупности согласно некоему условию. Подобные выборки могут быть независимыми (несвязанными) или зависимыми (связанными, сопряженными, парными). Сравнение связанных и несвязанных выборок производится с помощью разных критериев. Т-критерий Стьюдента – общее название для класса методов статистической проверки гипотез (статистических критериев), основанных на сравнении с распределением Стьюдента. Наиболее частые случаи применения t-критерия связаны с проверкой равенства средних значений в двух выборках. Для применения данного критерия необходимо, чтобы исходные данные имели нормальное распределение.
Сравнение двух связанных выборок для группы с острым течением заболевания. Критерий Стьюдента. Двусторонняя критическая область. Переменные: Var1, Var2. Объем выборки: N=13. T=3,52, число степеней свободы k=12. В среднем значения отличаются, X1ср.<>X2ср., на уровне значимости p=0,004. Сравнение двух связанных выборок для группы с подострым течением заболевания. Критерий Стьюдента. Переменные: Var1, Var2. Объем выборки: N=11. T=22,90, число степеней свободы k=10. В среднем значения отличаются, X1ср.<>X2ср., на уровне значимости p<0,001. Сравнение двух связанных выборок для группы с хроническим течением заболевания. Сравнение двух связанных выборок. Критерий Стьюдента. Двусторонняя критическая область. Переменные: Var1, Var2. Объем выборки: N=14. T=47,20, число степеней свободы k=13. В среднем значения отличаются, X1ср.<>X2ср., на уровне значимости p<0,001. Выдвигаем нулевую теорию, противоположную от целей задачи, то есть препарат не эффективен. Но при сравнении данных в программе Medstat, исследования являются статистически значимыми. В этом случае мы отвергаем нулевую теорию и принимаем альтернативную теорию. Вывод: Следовательно применение препарата МОВАЛИС является эффективным, то есть при применение препарата сокращается течение заболевания во всех исследуемых группах.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|







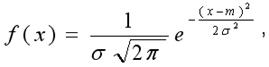 ()
()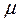 . Результат изменения
. Результат изменения  (
(  ).
). ) и дисперсией (
) и дисперсией (  );
); . В таком случае формула для определения среднего арифметического наблюдений
. В таком случае формула для определения среднего арифметического наблюдений 
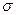 ) – это положительный квадратный корень из дисперсии (можно возвести в квадрат каждое отклонение и найти среднее возведенных в квадрат отклонений;). Оно вычисляется в тех же единицах (размерностях), что и исходные данные и характеризует степень рассеивания вариационного ряда вокруг средней. Чем меньше
) – это положительный квадратный корень из дисперсии (можно возвести в квадрат каждое отклонение и найти среднее возведенных в квадрат отклонений;). Оно вычисляется в тех же единицах (размерностях), что и исходные данные и характеризует степень рассеивания вариационного ряда вокруг средней. Чем меньше 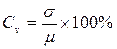
 наблюдается слабое разнообразие признака, при 10%<Cv<20% – среднее разнообразие признака, при
наблюдается слабое разнообразие признака, при 10%<Cv<20% – среднее разнообразие признака, при  – сильное разнообразие признака.
– сильное разнообразие признака.
 График для среднего нормального распределения.
График для среднего нормального распределения.