
|
|
ВОЗМОЖНЫЙ ПОДХОД К ОПЙИСАНИЮ ДИНАМИКИ СОЦИАЛЬНОЙ СИСТЕМЫВ настоящее время наиболее распространены методы управления, задача которых состоит в поддержании регулируемой величины на некотором заданном уровне (в экономике, например, может быть задан темп роста совокупного общественного продукта или темп роста реальных доходов населения и т.д.). Сущность программированного управления та же, так как при этом регулируемая величина поддерживается на уровне, являющемся заданной априорно функцией времени. Этот подход не может быть использован при экстремальном управлении, т.е. для решения задачи достижения максимального или минимального значения регулируемой величины, Обычно вид функциональной зависимости между регулируемой величиной (функцией) и регулирующей величиной (аргументом) неизвестен. К тому же часто влияние аргумента на Функцию само есть функция от времени, вид которой также неизвестен.
В основе принципа действия экстремальных регуляторов в технике лежит идея эксперимента, сочетающегося с использованием расчетного пути. Управляемая система разбивается на составляющие ее звенья. Определяется, для каких звеньев нужно построить действующий макет. Для остальных составляются уравнения состояния, выходного сигнала и др. Затем полученные результаты объединяются, чтобы рассчитать весь процесс управления. Часто построенная модель проигрывается на аналоговых или цифровых электронно-вычислительных устройствах. Вводится искусственное возмущение, проверяется направление течения процесса, и, если оно обеспечивает приближение регулируемой величины к требуемому экстремуму, возмущение допускается; если же происходит удаление, от экстремальной точки, знак возмущения меняется и т.д. После того как найдены характеристики объекта управления, решается задача статистической оптимизации управляющих сигналов. Здесь применяются различные вариационные методы, а также методы динамического программирования, принцип максимума Понтрягина и другие. Таким образом, в общих чертах уже наметились основные этапы пути, по которому необходимо пройти для решения задачи активного воздействия на результаты функционирования объекта исследования*. Это следующие этапы: а) анализ, б) описание, в) оптимизация, г) управление. Здесь будет рассмотрен вопрос описания деятельности объекта. Для удобства изложения последующего материала введем некоторые определения и обозначения. Ниже даны наиболее общие из них, поскольку специальные, относящиеся к частным вопросам, будут вводиться по мере необходимости. При постановке задачи анализа системы управления задается процесс. Под процессом понимается неизменяемая часть системы (управляемые объекты). Сигналы управления
ного процесса системы анализироваться не будет. В то время как инерционное запаздывание для целого ряда экономических и социальных задач, (на настоящем уровне их постановки) может не учитываться, анализ чистого запаздывания по времени (временного лага) влияния входного сигнала на регулируемую переменную обычно необходим. Поэтому введем еще две группы переменных. Переменные одной группы назовем эндогенными, а второй группы – предопределенными. К эндогенным переменным в момент времени t относятся переменные y(t) В группу предопределенных переменных z(t) входят все переменные x(t) и x(t - τ), или экзогенные переменные, а также и y(t - τ), или эндогенные переменные более ранних временных периодов (t - τ), где τ – длительность чистого запаздывания (t > τ =1,2,3...). После того как определены наиболее общие используемые понятия, можно дать первичную характеристику объекта изучения. Допустим, имеется некоторый функционирующий экономический или социальный процесс. Минимальную систему, включающую этот процесс, обозначим буквой S, а ее подсистемы – Sl, где Система S достаточно автономна в принятии решений, не ухудшающих в общем значения критерия эффективности управления системой σ; подсистема Sl автономна в принятии решений, не ухудшающих в общем значение критерия эффективности управления системой S. Следовательно, само управление сложной системой – сложная система. Основные ограничения на характеристики процесса следующие: 1. Рассматриваемый процесс должен быть по меньшей мере сводим к стационарному второго порядка. В то же время допускается отсутствие свойства эргодически. 2. Эндогенные переменные считаются линейными или линеаризуемыми функциями переменных – аргументов.
Во внимание принимаются только причинно связанные переменные, что предполагает наличие качественного теоретического описания динамического процесса. Введем следующие обозначения:
Здесь m – число эндогенных переменных (I = 1,2,..., m), n – число предопределенных переменных (j = 1,2,..., n), n = n1 + n2, где n1 – число эндогенных переменных, оказывающих влияние с чистым запаздыванием по времени (j1 = 1,2,…, n1)
n2 – число экзогенных переменных (j2 = 1,2,…, n2). Матрица A(t) состоит из структурных коэффициентов взаимозависимости между эндогенными переменными. Учитывается, что сила влияния одной из переменных на другую – величина, изменяющая во времени. Переменная zn+1(t) ≡ 1. Коэффициенты βi n+1(t) – столбец свободных членов в уравнении, который введен лишь по соображениям удобства чтения, поскольку в советской литературе более принята именно такая запись уравнений, Матрица В(t) состоит из структурных коэффициентов влияния предопределенных переменных на изменение значений эндогенных переменных. Коэффициенты в матрицах А(t) и В(t) могут быть равными нулю. Эти коэффициенты также являются функциями времени, а вектор ξ(t) – случайная переменная с конечной дисперсией и Е [ξ(t)] = 0. Он в основном состоит из собственного шума системы S плюс некоторая часть шума, поступающего на вход системы. Тогда динамический процесс системы имеет следующий вид: y(t) = A(t)y(t) + B(t)z(t) + ξ(t) (1) Предполагается отсутствие возможности проведения эксперимента. Можно привести следующий конкретный пример социальной системы, динамика которой описывается моделью (1). Допустим, изучается динамика вовлечения школьников дневных школ в общественное производство. Эндогенными переменными (y(t)) в данном случае могут считаться 3 доли уходящих из школы в отдельные сферы производства, доли уходящих по классам и т.д. В качестве экзогенных переменных (x(t)) могут быть приняты и профессии родителей, изменение престижа отдельных профессий и т.п. Пример эндогенной переменной с запаздыванием (y(t - τ)) реальный душевой доход в семьях ушедших школьников, в которых есть другие школьники. Модель (1) называется системой взаимозависимых уравнений. Переменные y(t), являющиеся функциями в одних уравнениях, выступают в качестве аргументов в других уравнениях. Это делает достаточно сложной задачу определения коэффициентов структуры А(t) и В(t). Впервые метод решения этой задачи для постоянных А и В предложен Тейлом [2]. Обычный метод наименьших квадратов для этой цели теоретически неприменим, так
как из-за взаимозависимости уравнений системы (1) коэффициенты стохастически связаны с случайными слагаемыми ξ(t) [3]. Свой метод Тейл назвал "двойным методом наименьших квадратов"* Для применения этого метода необходимо выполнение следующих предпосылок: 1. Система разрешима относительно взаимозависимых переменных (т.е. относительно эндогенных переменных с нулевым запаздыванием). Это условие эквивалентно тому, что существует преобразованная форма**. 2. Математические ожидания случайных слагаемых в структурных уравнениях равны нулю. Все случайные слагаемые не коррелированны; 3. Дисперсии и ковариации случайных слагаемых конечны и постоянны во времени. Покажем, как получить оценки структурных коэффициентов для одного уравнения из системы взаимозависимых уравнений [4]. Коэффициенты считаются не изменяющимися во времени. Расчет проведен для первого уравнения. Для остальных вычисления идентичны:
Здесь Н ≤ m-1 – число взаимозависимых переменных, причинно влияющих на y1t ; F – число предопределенных переменных, причинно влияющих на y1t; переменная zF+1 ≡ 1. Векторы коэффициентов a1t и b1j являются соответственно оценками α1t и β1j. Обозначим через Y1, вектор наблюденных значений переменной y1t(t=1,2,…,T), через YH – матрицу наблюденных значений пре
допределенных переменных, буквами a1 и b1, - векторы оценок параметров α1t и β1j. Эти два вектора могут быть вычислены из следующего уравнения:
где Вычислив векторы аi и bi для всех взаимозависимых переменных y1, y2,..., ym, получим матрицы A и B, не изменяющиеся во времени. Коэффициенты в них равны средним влияниям переменных-аргументов на эндогенные переменные, определенных для промежутка времени T, за который имеются данные. Это лишь приближенно соответствует действительности и неверно для длительного временного интервала. В известных из литературы попытках получить матрицы А(t) и B(t) используются разложение периода Т на ряд интервалов и построение для каждого из интервалов подобных структурных систем. Имеются попытки исследования изменчивости структуры по поведению отклонений фактических значений от расчетных и т.д. Но на этом пути встречаются трудности. Во-первых, резко возрастает статистически необходимое T во-вторых, усиливается значение правильности выбора формы связи между переменными. Системы с матрицами вида А и В в работе [5] отнесены к динамико-статистическим, а в работе [7] дан общий подход к построению матриц А(t) и B(t). Основная идея этого подхода – разложение временной последовательности в пространстве. При этом рассматривается поведение систем Sl в периоде Т. Динамический процесс системы Sl есть реализация некоторого случайного динамического процесса σl (l = 1,2,…,L), тогда как динамический процесс системы является определенной оценкой математического ожидания этого случайного процесса. Фиксируя t = 1, получаем его сечение, состоящее из набора взаимосвязанных и взаимозависимых величин с известным распреде-
лением. Применяя к этому сечению двойной метод наименьших квадратов, получим матрицы При этом подходе необходимый для статистической устойчивости структурных коэффициентов период T по крайней мере не длиннее, чем при расчете матриц А и В. Если там он определяется числом переменных (m+n), т.е. размерностью процесса, то здесь влияние этого ограничения резко ослабевает, тогда как обычно легко достигается удовлетворение условия L >> m+n. Влияние наибольшей длины чистого запаздывания max τ на минимально необходимое T в обоих случаях одинаково, при несомненном преимуществе второго подхода из-за возможности построения А(t) и B(t). Здесь считается, что сами структурные коэффициенты – величины неуправляемые. Это соответствует действительности во многих практических задачах. Но в случае необходимости можно провести исследование взаимосвязей между y(t), z(t) и А(t), B(t). Никаких принципиальных трудностей при этом не возникает. Рассмотрим далее некоторые частные проблемы: автокорреляцию случайных слагаемых, идентификацию и определение длительности чистого запаздывания. Уже в предпосылках возможности применения двойного метода наименьших квадратов предполагается отсутствие автокор-
реляции между случайными слагаемыми для различных моментов времени. Считается, что нарушение этой предпосылки снижает эффективность оценок структурных коэффициентов и может привести даже к их несостоятельности. Проведенные некоторыми статистиками эксперименты показали, что эти опасения сильно преувеличены. Для разрешимости системы, состоящей из взаимозависимых уравнений, относительно эндогенных переменных y(t) необходимо, чтобы каждое уравнение системы было по меньшей мере идентифицировано. Неидентифицированная система не может быть разрешена однозначно, а сверхидентифицированная требует проведения достаточно сложных расчетов. Необходимое и достаточное условие идентификации каждого уравнения следующее: уравнение идентифицировано, если Н+F = n+1. Весьма сложно определить время чистого запаздывания предопределенных переменных на эндогенные. Существует несколько подходов к решению этой задачи. Естественно, вначале делаются теоретические предположения о наличии таких запаздываний и их периоде. Затем проверяется согласие теории с эмпирическими выводами. При отсутствии таких предположений по ряду связей приходится доверять результатам их статистического анализа. В качестве одного из подходов может быть использован анализ нормированных автокорреляционных и корреляционных функций. Обсуждение других подходов к этой проблеме можно найти в работе [6].
Литература 1. Мерриэм К. Теория оптимизации и расчет систем управления с обратной связью. М., "Мир", 1967. 2. Theil H. Repeated Least-Squares Applied to Complete Equation Sistems. Central Planning Bureau. The Haque, 1952 3. Haavelmo T. The Statistical Implication of s System of Simultaneous Equations. – "Econometrica", 1943, №11. 4. Theil H. Economic Policy and Farecasts. Amsterdam, North Holland Publishing Co. 1958 5 Розанов Г.В., Френкель А.А. Некоторые вопросы статистического прогноза развитая отрасли. - В сб.; материалы Всесоюзной конференции по применению экономико-математических методов и электронно-вычислительной техники в планировании развития и размещения производства. Таллинн, 1967. 6. Malinvaud E. The Estimation of Distributed Lags: a Comment. – "Econometrica", 1961, vol. 29, №3 7 Розанов Г.В. Проблемы построения статистической динамической модели развития отрасли. - В сб.: Проблемы статистики. М., 1968.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 называются входными сигналами (или независимыми переменными) динамического процесса. Математическое описание динамики неизменяемой части системы называется динамическим процессом [1]. Выходные сигналы (зависимые переменные)
называются входными сигналами (или независимыми переменными) динамического процесса. Математическое описание динамики неизменяемой части системы называется динамическим процессом [1]. Выходные сигналы (зависимые переменные)  представляют собой отклики на входные сигналы. Рассматриваемая ниже система считается безынерционной (в целях упрощения), поэтому качество переход -
представляют собой отклики на входные сигналы. Рассматриваемая ниже система считается безынерционной (в целях упрощения), поэтому качество переход - . В то же время
. В то же время  . Легко найти физическое выражение перечисленных систем: если система S – отрасль (школьники Западной Сибири), то Sl – предприятие (школьники Новосибирска), σ - вся промышленность (школьники всей Сибири). Управлению в первом случае может подлежать, например, процесс производства отрасли, во втором – процесс выбора специальности.
. Легко найти физическое выражение перечисленных систем: если система S – отрасль (школьники Западной Сибири), то Sl – предприятие (школьники Новосибирска), σ - вся промышленность (школьники всей Сибири). Управлению в первом случае может подлежать, например, процесс производства отрасли, во втором – процесс выбора специальности.


 (2)
(2) (3)
(3) (4)
(4)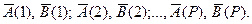 Штрих над каждой матрицей означает, что она получена из сечения. Здесь Р = Т – max τ. Аппроксимируя каждый из коэффициентов матриц как функцию от времени (обычным методом наименьших квадратов), получим матрицы А0(t) и B0(t), в которых уже записаны для всех структурных коэффициентов их функции от времени. Нуль около каждой матрицы означает, что они получены по данным периода Т. Эти матрицы экстраполируются на моменты времени T + 1, T + 2,.... Экстраполированные матрицы обозначим А1(Р+1), В1(Р+1); А1(Р+2), B1(P+2).... Единица вверху означает число оценок этих матриц. После наступления момента времени (T+1) по полученной информации рассчитываются
Штрих над каждой матрицей означает, что она получена из сечения. Здесь Р = Т – max τ. Аппроксимируя каждый из коэффициентов матриц как функцию от времени (обычным методом наименьших квадратов), получим матрицы А0(t) и B0(t), в которых уже записаны для всех структурных коэффициентов их функции от времени. Нуль около каждой матрицы означает, что они получены по данным периода Т. Эти матрицы экстраполируются на моменты времени T + 1, T + 2,.... Экстраполированные матрицы обозначим А1(Р+1), В1(Р+1); А1(Р+2), B1(P+2).... Единица вверху означает число оценок этих матриц. После наступления момента времени (T+1) по полученной информации рассчитываются  , а затем А1(t) и B1(t). По этим матрицам опять вычисляются А2(Р+2), В2(Р+2); А2(Р+3), B2(P+3),.... В случае высокой точности А0(t) и B0(t) перерасчет может производиться реже, чем раз в единицу времени.
, а затем А1(t) и B1(t). По этим матрицам опять вычисляются А2(Р+2), В2(Р+2); А2(Р+3), B2(P+3),.... В случае высокой точности А0(t) и B0(t) перерасчет может производиться реже, чем раз в единицу времени.