
|
|
НОВЫЙ ПОДХОД К ОБРАБОТКЕ СОЦИОЛОГИЧЕСКОЙ ИНФОРМАЦИИ
Данные социологического обследования можно представить следующим образом. Имеется конечное множество объектов
причем каждый объект Предполагается, что каждый признак
где Каждый признак Полезно различать следующие типы признаков. Признак p называется количественным, если его значения-
ми Признак p называется качественным, если его значения Признак p относится к классификационным, если его значения не являются числами и не связаны естественным упорядочением. К классификационным признакам можно отнести пол, профессию, причину отъезда из данного города и т.д. Существующие методы обработки данных социологического обследования связаны в основном с обработкой количественных признаков. Качественные признаки обычно при обработке сводят к количественным (иногда неявно), приписывая их значениям баллы, и применяют далее статистические методы. Например, коэффициент ранговой корреляции для качественных признаков является обычным коэффициентом корреляции для числовых признаков, полученных приписыванием соответствующих баллов значениям данных качественных признаков. Статистическая обработка таких балльных признаков (например, подсчет среднего значения, дисперсии и т.д.) встречает сильные возражения, поскольку приписанные баллы, вообще говоря, характеризуют лишь упорядочение значений признака, и применение к ним арифметических операций требует обоснования в каждом конкретном случае. Исследование вопросов, связанных с таким обоснованием, потребовало пересмотра и значительного углубления концепции измерения. Полученные к 1963 г. результаты были подытожены в переведенном на русский язык сборнике[2], из которого видно, что разработка обоснования находится пока в зачаточной стадии. Еще более неясны вопросы, связанные с обработкой классификационных признаков. Иногда значения классификационного признака предварительно упорядочивают ( приписывая баллы) в соответствии с какой-либо содержательной гипотезой (например, по их частости) или мнениями экспертов. В некоторых случаях рас-
сматривают статистические показатели, которые имеют смысл и для классификационных признаков (например, мода или энтропия распределения). Иногда, основываясь на эвристических соображениях вводят специальные показатели. Например, наиболее употребительными показателями связи классификационных признаков являются коэффициенты Пирсона и Чупрова [1], которые, по существу, оценивают статистическую значимость отличия n-мерного эмпирического распределения от теоретического равномерного. Предполагается, что, чем более эмпирическое распределение отличается от равномерного, тем теснее связаны признаки. В основе этих коэффициентов лежит подсчет величины Таких эвристических показателей можно ввести много, а какой предпочесть — неясно. Таким образом, существующие методы обработки данных ориентированы в основном на количественные признаки. Это заставляет исследователя для комплексной обработки данных использовать количественные или балльные, качественные признаки. Между тем классификационные признаки играют существенную роль в характеристике социологических объектов. Поэтому представляет интерес разработка специального аппарата для обработки классификационных признаков. Такой аппарат должен решать широкий круг задач с единой точки зрения. Заметим, что при обработке данных в терминах классификационных признаков потребуется иногда для единообразия результатов рассматривать количественные и качественные признаки как классификационные (аналогично тому, как теперь часто сводят к количественным признаки других типов). При этом часть информации будет теряться. Однако, поскольку количество значений признаков социологических объектов, как правило, несравнимо меньше объема N обследованных объектов, основная информация о признаках содержится в соответствующих им разбиениях и теряемая информация невелика. В то же время существующие методы обработки, сводящие признаки к количественным, привлекают дополнительную информацию о неколичественных признаках, истинность которой, как правило, очень мало обоснована.
Далее мы рассмотрим возможный путь создания аппарата обработки классификационных признаков, дающего единообразные методы решения широкого круга задач. Информация о классификационном признаке p, собранная при обследовании множества n, задается разбиением Мы считаем, что основным инструментом при обработке классификационных признаков должна служить количественная мера близости разбиений данного множества n. Меру близости разбиений Одно из этих условий состоит в том, чтобы Приведем точную формулировку первого условия. Аксиома I . Мера а) б) в) для любых разбиений
причем точное равенство достигается, только если разбиение
жит между разбиениями Следующая аксиома продиктована требованием равноправия всех объектов Аксиома 2. Если разбиение Потребуем теперь, чтобы при частичном совпадении разбиений Аксиома 3. Если разбиения Последняя аксиома дает масштаб измерения. Аксиома 4. Максимальное расстояние между разбиениями множества n равно Имеет место следующий результат [3]. Теорема. Мера Можно проверить, что аксиомы 1-4 выполняются для следующей меры:
1, если где Аналогично определяются величины Таким образом, если признать аксиомы 1-4 естественными, то Подобно тому как в геометрическом пространстве для нескольких зафиксированных точек можно находить центр тяжести, так и в множестве всех разбиений на n , геометризованном мерой
Рассмотрим теперь некоторые задачи обработки данных социологического обследования и методы их решения в терминах меры
Под классификацией ( таксономией) обычно понимают разбиение обследованной совокупности на группы объектов, "похожих" в выбранной системе признаков. В нашей терминологии классификация — это разбиение множества и на классы "близких' по системе признаков Если система состоит из одного признака
Заметим, что для применения данного метода классификации в отличие от известных сейчас методов [4] не нужно знание расстояний между объектами Аналогичным образом, если имеется насколько классификаций данного множества по разным системам признаков, то классификацию по всем признакам одновременно находим как усредненное разбиение по отношению к данным разбиениям.
Пусть N объектов уже расклассифнцированы в соответствии c принимаемыми ими значениями признаков Для решения этой задачи нужно присоединить (N+1)-й объект к первоначальной совокупности, рассмотреть разбиения Заметим, что при малом N разбиение
Содержательные соображения показывают, что близкие признаки характеризуются близкими разбиениями. Поэтому примем меру близости признаков Тогда в соответствии с формулой (*)
Тот факт, что Заметим, что
Пусть на множестве n задано некоторое разбиение Абсолютная значимость признака Здесь, как обычно, значимость признака понижается в смысле его информативности. Однако при конкретных исследованиях такую значимость часто трактуют как "силу влияния" признака P на фактор, порождающий разбиение
Рассмотрим задачу измерения относительно независимых факторов по данной системе зависимых признаков. Такая задача обычно решается для количественных признаков методами факторного анализа: по данным признакам В случае классификационных признаков поступим следующим образом. Составим матрицу
0ни, правда, лишь относительно независимы, но и в факторном анализе такая же ситуация: равенство корреляции о лишь необходимое, но не достаточное условие независимости. Зато здесь облегчается содержательная интерпретация факторов, поскольку они являются группами признаков. Разбиения, соответствующие факторам, получаются как усредненные разбиения по отношению к множествам признаков, составляющих факторы. Зная эти разбиения, можно, например, оценивать значимость факторов методом Отличительной чертой приведенных методов обработки по сравнению с существующими является то ,что они дают возможность решать широкий класс задач в рамках единого подхода, основанного на четких аксиоматических построениях. Понятно, что в данной работе лишь намечен каркас аппарата обработки данных с единой точки зрения: не приведены необходимые алгоритмы, нет статистической разработки оценки "доверия" к получаемым по выборке результатам и т.д. При этом перспективность намеченного подхода комет быть доказана лишь успешным применением его в конкретных исследованиях. На этом пути сделаны лишь первые шаги. На материалах обследования приживаемости населения в районах, нового промышленного освоения (руководитель канд.экон.наук Е.Д. Малинин) использовался метод А имеющиеся отклонения позволяют сделать выводы, подтверждаемые другими данными. Например, город, для которого значимость признака "удовлетворенность общественным питанием" существенно выше, чем в других городах, и реально значительно хуке обеспечен столовыми. Не совсем тривиальным является вывод, что субъективное мнение опрошенных о том, как влияют их доходы на их приживаемость, довольно далеко от реального влияния (оказалось, что признак "Доход на одного члена семьи" относится к наиболее значимым, тогда как признак " Удовлетворен ли материальным состоянием семьи?" относится к наименее значимым).
Другой эксперимент был связан с нахождением усредненной экспертной оценки. Учителя из некоторой совокупности оценивались по мастерству тремя экспертами: директором, завучем и коллегой-учителем. Таким образом, имелось три разбиения множества учителей на группы учителей с одинаковой оценкой эксперта. Описанным методом былонайдено усредненное разбиение, которое должно символизировать собой некоторого объективного эксперта. Была проделана следующая проверка объективности найденного разбиения. Каждый из трех сотрудников Института экономики и организации промышленного производства СО АН СССР нашел усредненную оценку самостоятельно, на основе интуитивных соображений, для некоторой случайной выборки из обследованной совокупности. Оказалось, что полученное разбиение лежит в центре сферы (в геометрическом пространстве разбиений), на которой находятся остальные три усредненных разбиения, выполненные на основе интуитивных соображений. Результат эксперимента можно интерпретировать следующим образом. Наше разбиение находится в центре, так как оно в некотором смысле представляет собой объективную оценку, а остальные разбиения дают разброс по отношению к нему в результате флуктуаций, присущих субъективным оценкам.
Литература
1. Юл Д.Э., Кендэл М.Д. Теория статистики. М., 1960.. 2. Психологические измерения. М., 1967 3. Миркин Б.Г., Черный Л.Б. Об измерении расстояния между разбиениями конечного множества. – В сб.: Математические методы моделирования и решения экономических задач. Новосибирск, «Наука», 1969. 4. Распознавание образов в социальных исследованиях. Новосибирск, «Наука», 1968. 5. Лазарсфельд П. Логические и математические основания латентно-структурного анализа. – В сб.: Математические методы в современной буржуазной социологии. М., 1966. 6. Лоули Д., Максвелл А. Факторный анализ как статистический метод. М., 1967. 7. Черный Л.Б. Обобщение метода последовательных расчетов в одной задаче классификации. – В сб.: Математические модели и методы в социально-экономических исследованиях. Новосибирск, 1968.
В.Л. Устюжанинов 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|

 характеризуется значениями признаков
характеризуется значениями признаков  . Например, признаками могут быть возраст, пол, профессия, удовлетворенность своей работой и т. д.
. Например, признаками могут быть возраст, пол, профессия, удовлетворенность своей работой и т. д. может принимать
может принимать  значений:
значений:  Таким образом, каждый объект
Таким образом, каждый объект  характеризуется упорядоченным набором
характеризуется упорядоченным набором
 - значение признака
- значение признака  соответствующее объекту
соответствующее объекту 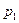 - профессия,
- профессия,  - пол,
- пол,  - возраст, то некоторый объект может характеризоваться набором: (токарь, женский, 26 лет).
- возраст, то некоторый объект может характеризоваться набором: (токарь, женский, 26 лет). во второй – объекты
во второй – объекты  и так далее, а последний класс состоит из объектов
и так далее, а последний класс состоит из объектов  Это разбиение будем обозначать
Это разбиение будем обозначать 
 , являются числа. Таковы, например, возраст, зарплата и т.д.
, являются числа. Таковы, например, возраст, зарплата и т.д. , а эта величина указывает лишь на значимость отличия эмпирического распределения от теоретического, но не степень этого отличия.
, а эта величина указывает лишь на значимость отличия эмпирического распределения от теоретического, но не степень этого отличия.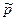 на классы объектов, отвечающих одним и тем же значениям признака. Поэтому вопрос об изучении признаков сводится к изучению соответствующих разбиений.
на классы объектов, отвечающих одним и тем же значениям признака. Поэтому вопрос об изучении признаков сводится к изучению соответствующих разбиений. обозначим
обозначим  и потребуем, чтобы она удовлетворяла некоторым условиям.
и потребуем, чтобы она удовлетворяла некоторым условиям. и
и  ( т.е. классы
( т.е. классы  совпадают с классами
совпадают с классами  );
); ;
;

 ле-
ле-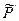 получено из разбиения
получено из разбиения  - из
- из 
 , являющегося сегментом2) их обоих, то
, являющегося сегментом2) их обоих, то  3).
3). (*)
(*) находятся в одном классе
находятся в одном классе  { 0, если
{ 0, если 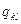 ( для
( для  . Расстоянием от разбиения
. Расстоянием от разбиения  . Усредненным разбиением по отношению к {
. Усредненным разбиением по отношению к {  , для которого это расстояние минимально, т.е.
, для которого это расстояние минимально, т.е.
 Классификация.
Классификация. объектов
объектов  , то классификацией является соответствующее разбиение
, то классификацией является соответствующее разбиение  ,если имеется да признака
,если имеется да признака  и
и  , то классификация - это разбиение, среднее для
, то классификация - это разбиение, среднее для  . В общем случае (для т признаков) мы предлагаем в качестве классификации брать усредненное ( в вышеопределенном смысле) разбиение
. В общем случае (для т признаков) мы предлагаем в качестве классификации брать усредненное ( в вышеопределенном смысле) разбиение 
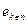 . Именно определение расстояний меду между
. Именно определение расстояний меду между  Распознавание образов [4].
Распознавание образов [4]. , согласно которому и следует классифицировать (N+1)-й объект.
, согласно которому и следует классифицировать (N+1)-й объект. Оценка взаимосвязи признаков.
Оценка взаимосвязи признаков. пропорциональной мере близости соответствующих разбиений
пропорциональной мере близости соответствующих разбиений  (**)
(**) , означает, что признаки P и Q дублируют друг друга;
, означает, что признаки P и Q дублируют друг друга;  означает, что признаки P и Q независимы.
означает, что признаки P и Q независимы. и в разных классах другого разбиения. Легко доказать несмещенность [I] этой оценки.
и в разных классах другого разбиения. Легко доказать несмещенность [I] этой оценки. Оценка значимости признаков.
Оценка значимости признаков. .
. .
. . Измерение скрытых признаков (латентный анализ [5]).
. Измерение скрытых признаков (латентный анализ [5]). строятся их линейные комбинации
строятся их линейные комбинации  (факторы), корреляция между которыми равна 0[6].
(факторы), корреляция между которыми равна 0[6]. расстояний между признаками и разобьем признаки
расстояний между признаками и разобьем признаки  .
.