
|
|
Равносильные формулы алгебры логикиОпределение.Две формулы алгебры логики А и В называются равносильными, если они принимают одинаковые логические значения на любом наборе значений входящих в формулы элементарных высказываний. Равносильность формул будем обозначать знаком ≡, а запись А ≡ В означает, что формулы А и В равносильны. Формула А называется тождественно истинной (или тавтологией), если она принимает значение 1 при всех значениях входящих в неё переменных. Формула А называется тождественно ложной, если она принимает значение 0 при всех значениях входящих в неё переменных. Ясно, что отношение равносильности рефлексивно, симметрично и транзитивно. Между понятиями равносильности и эквивалентности существует следующая связь: если формулы А и В равносильны, то формула А↔В – тавтология, и обратно, если формула А↔В – тавтология, то формулы А и В равносильны. Важнейшие равносильности алгебры логики можно разбить на три группы.
10. Х&(у 11. х 12. Х 13. Х
Докажем один из законов поглощения. Рассмотрим формулу А 2. Равносильности, выражающие одни логические операции через другие: 1. х 2. х 3. 4.
5. х&у
6.х Ясно, что равносильности 5 и 6 получаются из равносильностей 3 и 4 соответственно, если от обеих частей последних взять отрицания и воспользоваться законом снятия двойного отрицания. Таким образом, в доказательстве нуждаются первые четыре равносильности. Докажем две из них: первую и третью. Так как при одинаковых логических значениях х и у истинными являются формулы х↔у, х→у, у Пусть теперь х и у имеют различные логические значения. Тогда будут ложными эквивалентность х↔у и одна из двух импликаций х→у или у Рассмотрим равносильность 3. Если х и у принимают одновременно истинные значения, то будет истинной конъюнкция х&у и ложным отрицание конъюнкции Пусть теперь хотя бы одна из переменных х или у принимает значение ложь. Тогда будет ложной конъюнкция х&у и истинной её отрицание. В то же время отрицание хотя бы одной из переменных будет истинным, а поэтому будет истинной и дизъюнкция Следовательно, во всех случаях обе части равносильности 3 принимают одинаковые логические значения. Из равносильностей этой группы следует, что всякую формулу алгебры логики можно заменить равносильной ей формулой, содержащей только две логические операции: конъюнкцию и отрицание или дизъюнкцию и отрицание. Дальнейшее исключение логических операций невозможно. Так, если мы будем использовать только конъюнкцию, то уже такая формула как отрицание х не может быть выражена с помощью операции конъюнкции. Однако существуют операции, с помощью которых может быть выражена любая из пяти логических операций, которыми мы пользуемся. Такой операцией является, например, операция «Штрих Шеффера». Эта операция обозначается символом х
Очевидно, имеют место равносильности: 1) 2) х&у Из этих двух равносильностей следует, что всякая формула алгебры логики может быть заменена равносильной формулой, содержащей только операцию «Штрих Шеффера». Отметим, что х Аналогично может быть введена операция 3. Равносильности, выражающие основные законы алгебры логики:
Докажем последний из перечисленных законов. Если х = 1, то будут истинными формулы х Пусть теперь х = 0. Тогда х

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
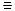 х – закон идемпотентности;
х – закон идемпотентности;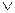 х
х  0
0 х&
х& 
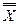
 )- первая формула расщепления.
)- первая формула расщепления. у
у  у)&(у
у)&(у 

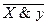

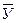


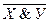 . В то же время будут ложными и
. В то же время будут ложными и 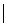 у и определяется следующей таблицей истинности:
у и определяется следующей таблицей истинности: (х, у)
(х, у) 