
|
|
Логические операции над высказываниямиВведение Изучение законов человеческого мышления является предметом логики. Как самостоятельная наука логика оформилась в трудах греческого философа Аристотеля (384 – 322 до н.э.). Впервые в истории идеи о построении логики на математической основе были высказаны немецким математиком Г. Лейбницем (1646 - 1716) в конце 17 века. Современная математическая логика определяется как раздел математики, посвященный изучению математических доказательств и вопросов основания математики. Отличительная черта математической логики – использование доказательств, а не наблюдений. Одной из основных причин развития математической логики является широкое распространение аксиоматических методов в построении различных математических теорий. Математическая теория, непротиворечивость которой требовалось доказать, стала предметом другой математической теории, которую Гильберт назвал математической, как теорию доказательств. Выбирая по–разному системы аксиом и правила вывода одних формул из других, получают различные синтаксические логические теории. Современная математическая логика включает два основных раздела: логику высказываний и охватывающей её логику предикатов, для построения которых существует два языка(подхода), образующих два варианта формальной логики: алгебру логики и логические исчисления.
Основным понятием математической логики является понятие «простого высказывания». Под высказыванием обычно понимают всякое повествовательное предложение, утверждающее что-либо о чем-либо, и при этом мы можем сказать, истинно оно или ложно в данных условиях места и времени. Логическими значениями высказываний являются «истина» и «ложь». Высказывание, представляющее собой одно утверждение, принято называть простым или элементарным. Высказывания, которые получаются из элементарных с помощью грамматических связок «не», «и», «или», «если…, то…», «тогда и только тогда», принято называть сложными или составными. В алгебре логики все высказывания рассматриваются только с точки зрения их логического значения, а от их житейского содержания отвлекаются. Считается, что каждое высказывание либо истинно, либо ложно и ни одно высказывание не может быть одновременно истинным и ложным. В дальнейшем будем элементарные высказывания обозначать малыми буквами латинского алфавита: x, y, z, ..., a, b, c, ...; истинное значение высказывания – буквой и или цифрой 1, а ложное значение – буквой л или цифрой 0. Если высказывание а истинно, то будем писать а=1, а если а ложно, то а =0.
Логические операции над высказываниями
2. Конъюнкция(логическое умножение). Конъюнкцией двух высказываний х, у называется новое высказывание, которое считается истинным, если оба высказывания х, у истинны, и ложным, если хотя бы одно из них ложно.
Логические значения конъюнкции описываются следующей таблицей истинности:
Из определения операции конъюнкции и отрицания ясно, что высказывание х&
4. Импликация.Импликацией двух высказываний х, у называется новое высказывание, которое считается ложным, если х истинно, а у – ложно, и истинным во всех остальных случаях. Импликация высказываний х, у обозначается символом х→у, читается «если х, то у» или «из х следует у». Высказывание х называют условием или посылкой, высказывание у – следствием или заключением, высказывание х→у – следованием или импликацией. Логические значения операции импликации описываются следующей таблицей истинности:
Употребление слов «если …, то …» в алгебре логики отличается от употребления их в обыденной речи, где мы, как правило, считаем, что, если высказывание х ложно, то высказывание «если х, то у» вообще не имеет смысла. Кроме того, строя предложение вида «если х, то у» в обыденной речи, мы всегда подразумеваем, что предложение у вытекает из предложения х. Употребление слов «если …, то …» в математической логике не требует этого, поскольку в ней смысл высказываний не рассматривается. Импликация играет важную роль в математических доказательствах, так как многие теоремы формулируются в условной форме «если х, то у». Если при этом известно, что х истинно и доказана истинность импликации х→у, то мы вправе сделать вывод об истинности заключения у. 5. Эквиваленция.Эквиваленцией (или эквивалентностью) двух высказываний х, у называется новое высказывание, которое считается истинным, когда оба высказывания х, у либо одновременно истинны, либо одновременно ложны, и ложным во всех остальных случаях. Эквиваленция высказываний х, у обозначается символом х↔у, читается «для того, чтобы х, необходимо и достаточно, чтобы у» или «х тогда и только тогда, когда у». Высказывания х, у называются членами эквиваленции. Логические значения операции эквиваленции описываются следующей таблицей истинности:
Эквивалентность играет важную роль в математических доказательствах. Известно, что значительное число теорем формулируется в форме необходимых и достаточных условий, то есть в форме эквивалентности. В этом случае, зная об истинности или ложности одного из двух членов эквивалентности и доказав истинность самой эквивалентности, мы заключаем об истинности или ложности второго члена эквивалентности.
Формулы алгебры логики С помощью логических операций над высказываниями можно строить различные новые, более сложные высказывания. Обычно при этом порядок операций указывается скобками. Определим понятие формулы логики высказываний. Первой частью любой формальной системы является ее язык. Чтобы определить язык, нужно прежде всего определить алфавит и его символы. Алфавитом будем называть любое непустое множество. Элементы этого множества называются символами данного алфавита. Любая конечная последовательность символов алфавита называется словом, или выражением, данного языка. Алфавит логики высказываний содержит такие символы: высказывания — буквы латинского алфавита с индексом или без него, логические связки ^, v, —>, <->, - , разделители (,). Слово в алфавите логики высказываний называется формулой, если оно удовлетворяет следующим условиям; 1. Любое высказывание (высказывательное переменное) — формула. 2. Если А и В формулы, то не А, А ^ В, A v В, А —> В, А <-> В — тоже формулы. Подформулой формулы А называется любое подслово А, само являющееся формулой. Таким образом, из приведенного формального определения формулы как определенной конструкции языка алгебры логики можно определить более простое понятие формулы. Всякое сложное высказывание, которое может быть получено из элементарных высказываний с помощью логических связок, называется формулой алгебры логики. Формулы алгебры логики обозначаются большими буквами латинского алфавита A, В, С,.., При этом скобки можно опускать, придерживаясь следующих правил: конъюнкция выполняется прежде всего, дизъюнкция выполняется второй, импликация и эквиваленция равноправны и выполняются последними. Каждая формула алгебры логики принимает свое логическое значение, которое определяется логическими значениями входящих в нее элементарных высказываний. Например, составим таблицу истинности для формулы (X ->Y)-> (X^
Если формула состоит из п элементов, то ее таблица истинности состоит из 2" строк. Приписывание значений истинности или ложности высказываниям, входящим в формулу, называется интерпретацией этих высказываний. Под интерпретацией формулы понимается приписывание значений истинности высказываниям, входящим в эту формулу.
С помощью логических операций над высказываниями из заданной совокупности высказываний можно строить сложные различные высказывания. При этом порядок выполнения операций указывается скобками. Всякое сложное высказывание, которое может быть получено из элементарных высказываний посредством применения логических операций отрицания, конъюнкции, дизъюнкции, импликации и эквивалентности, называется формулой алгебры логики. Формулы алгебры логики будем обозначать большими буквами латинского алфавита А, В, С, … Для упрощения записи формул принят ряд соглашений. Скобки Логическое значение формулы алгебры логики полностью определяется логическими значениями входящих в неё элементарных высказываний. Все возможные логические значения формулы, в зависимости от значений входящих в неё элементарных высказываний, могут быть описаны полностью с помощью таблицы истинности. Если формула содержит п элементарных высказываний, то она принимает 2 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 §1. Понятие высказывания.
§1. Понятие высказывания. 
 и читается «не х» или «неверно, что х». Логические значения высказывания
и читается «не х» или «неверно, что х». Логические значения высказывания  х
х
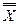 , которое называется двойным отрицанием высказывания х. Ясно, что логические значения высказывания
, которое называется двойным отрицанием высказывания х. Ясно, что логические значения высказывания  у),читается «х и у».Высказываниях, уназываются членами конъюнкции.
у),читается «х и у».Высказываниях, уназываются членами конъюнкции.

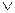 у,читается «х или у». Высказывания х, уназываются членами дизъюнкции. Логические значения дизъюнкции описываются следующей таблицей истинности:
у,читается «х или у». Высказывания х, уназываются членами дизъюнкции. Логические значения дизъюнкции описываются следующей таблицей истинности: v
v  можно опускать, придерживаясь следующего порядка действий: конъюнкция выполняется раньше, чем все остальные операции, дизъюнкция выполняется раньше, чем импликация и эквиваленция. Если над формулой стоит знак отрицания, то скобки тоже опускаются.
можно опускать, придерживаясь следующего порядка действий: конъюнкция выполняется раньше, чем все остальные операции, дизъюнкция выполняется раньше, чем импликация и эквиваленция. Если над формулой стоит знак отрицания, то скобки тоже опускаются. значений, состоящих из нулей и единиц, или, что то же, таблица содержит 2
значений, состоящих из нулей и единиц, или, что то же, таблица содержит 2