
|
|
Распределение Максвелла по абсолютным значениям скорости.
6.5. Функция распределения по скоростям.
Пусть система состоит из большого числа невзаимодействующих молекул, и нет внешних полей, тогда мы интересуемся только вероятностью
где Каждую частицу можно рассматривать как квазинезависимую подсистему, поэтому фазовый объем системы распадается на произведение множителей, каждый из которых определяет фазовый объем для отдельной молекулы:
а вероятность нахождения системы в состоянии с энергией
Поскольку все частицы одинаковы, то искомую вероятность можно записать в виде произведения:
где величина
Элемент объема
Итак, функция распределения по кинетическим энергиям для одной молекулы имеет вид:
Вероятность молекуле иметь кинетическую энергию в интервале от
Вероятность молекуле иметь кинетическую энергию в интервале от
Фазовый объем, соответствующий кинетической энергии, лежащей в диапазоне от
Тогда вероятность того, что молекула будет иметь кинетическую энергию от
Иногда бывает удобнее определить ту же вероятность, записав её через возможные значения скоростей:
Отметим, что температура Постоянную
Для вычислений используем известный табличный интеграл - интеграл Пуассона:
Тогда, положив в (2.11)
или
Отсюда
Окончательно получаем
Полученное выражение (2.14) – распределение Максвелла по скоростям – определяет вероятность того, что скорость молекулы лежит в диапазоне значений от По поводу этого распределения Больцман писал: «Устанавливающееся само собой наиболее вероятное распределение, которое мы называем распределением Максвелла по скоростям (ибо он первый нашел для него математическое выражение в специальном случае), не соответствует какому-то особому состоянию, противопоставляемому бесконечно бо/льшему набору других состояний, соответствующих немаксвелловским распределениям. Скорее, напротив, для подавляющего числа возможных состояний характерно распределение Максвелла, и число возможных распределений скоростей, существенно отличающихся от максвелловского, исчезающе мало».
2.2. Свойства распределения Максвелла. 1). Вероятность, или лучше плотность вероятности
скорости распределения по скоростям имеет максимум.
Наиболее вероятная скорость растет с температурой: молекула имеет скорость в окрестности уменьшается.
Если площадь под кривой нормирована на единицу, то площадь заштрихованной области (см. предыдущий рис.) равна вероятности
2.3. Характерные средние скорости.
1).Средняя скорость. По определению
Замена переменных:
Далее интегрируем по частям (
2). Средняя квадратичная скорость.
По определению:
Вспомним, что
Здесь
И средняя квадратичная скорость равна
Используя (2.18), можно получить среднюю кинетическую энергию молекулы:
характерных скоростей функции распределения
Рассмотрим подсистему, содержащую
где
а Тогда вероятность обнаружить молекулу со скоростями от
по скоростям в подсистеме из рисунке. Для подсистемы, состоящей из одной молекулы, максимум функции распределения довольно широк. Это отражает большой разброс в абсолютных значениях скоростей молекулы. Одна (1!) молекула - подсистема, которая содержит малое число частиц, поэтому флуктуации велики. Для подсистемы из распределения которого уменьшается как Фазовый объем
Тогда вероятность системе, состоящей из
как показано на рисунке, имеет резкий максимум при

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 . Кинетическая энергия системы равна сумме кинетических энергий образующих её частиц:
. Кинетическая энергия системы равна сумме кинетических энергий образующих её частиц: , (6.25)
, (6.25) - кинетическая энергия молекулы.
- кинетическая энергия молекулы. , (6.26)
, (6.26) равна
равна .
. , (6.27)
, (6.27) – пропорциональна распределению вероятностей по абсолютным значениям скоростей для каждой отдельной молекулы, где
– пропорциональна распределению вероятностей по абсолютным значениям скоростей для каждой отдельной молекулы, где ,
,  . (6.28)
. (6.28) , можно представить в виде:
, можно представить в виде: или
или  .
. . (2.5)
. (2.5) , обладая при этом определенными проекциями импульсов (
, обладая при этом определенными проекциями импульсов (  ), равна
), равна . (2.6)
. (2.6) ), равна
), равна . (2.7)
. (2.7)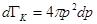 или
или  . (2.8)
. (2.8) . (2.9)
. (2.9) . (2.10)
. (2.10) во всех приведенных выражениях определяется по энергетической шкале и связана с термодинамической температурой
во всех приведенных выражениях определяется по энергетической шкале и связана с термодинамической температурой  как
как  .
. найдем из условия нормировки, взяв интеграл по всем возможным скоростям молекул, лежащим в пределах от
найдем из условия нормировки, взяв интеграл по всем возможным скоростям молекул, лежащим в пределах от  до
до 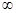 :
: . (2.11)
. (2.11) . (2.12)
. (2.12) и
и 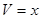 , находим
, находим ,
, .
. . (2.13)
. (2.13) , (2.14)
, (2.14) до
до  , или в шаровом слое фазового пространства скоростей от
, или в шаровом слое фазового пространства скоростей от  , имеет максимум при некоторой скорости молекулы. Действительно, фазовый объем растет пропорционально
, имеет максимум при некоторой скорости молекулы. Действительно, фазовый объем растет пропорционально  , а экспоненциальный множитель быстро убывает с увеличением скорости молекулы.
, а экспоненциальный множитель быстро убывает с увеличением скорости молекулы. Построим график функции
Построим график функции  и найдем значение
и найдем значение , при которой плотность вероятности
, при которой плотность вероятности .
.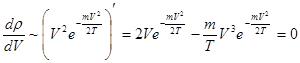 ;
; ;
;  . (2.15)
. (2.15)
 , а вероятность того, что
, а вероятность того, что ,
, того, что скорость молекулы лежит в пределах от
того, что скорость молекулы лежит в пределах от  до
до  , то
, то ,
, 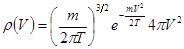 . (2.16)
. (2.16) .
. ,
,  дает
дает .
. ;
;  ,
,  ):
):
 ,
, .
. . (2.17)
. (2.17) .
.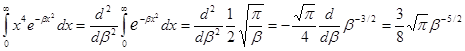 .
. . Откуда
. Откуда .
. . (2.18)
. (2.18)
 . (2.19)
. (2.19) под кривой
под кривой одинаковых невзаимодействующих частиц. Обозначим через
одинаковых невзаимодействующих частиц. Обозначим через  вероятность того, что такая подсистема обладает энергией в интервале от
вероятность того, что такая подсистема обладает энергией в интервале от  , (2.20)
, (2.20) ,
, – фазовый объем подсистемы, состоящей из одной молекулы, равный в пространстве скоростей
– фазовый объем подсистемы, состоящей из одной молекулы, равный в пространстве скоростей  . (2.21)
. (2.21) Плотность вероятности
Плотность вероятности 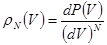 распределения
распределения имеет резкий максимум, ширина
имеет резкий максимум, ширина .
. , который может быть представлен как
, который может быть представлен как .
. ,
, а соответствующая ей функция распределения
а соответствующая ей функция распределения  ,
, .
.