
|
|
Вывод распределения Гиббса.МОЛЕКУЛЯРНАЯ ФИЗИКА Распределение Гиббса Вывод распределения Гиббса.
Распределение Гиббса определяет вероятность обнаружить макроскопическое тело, находящееся в термодинамическом равновесии с окружающей средой, в состоянии с заданной энергией
6.1. Функция распределения Гиббса. Задачей настоящего параграфа является нахождение явного вида функции распределения
Эта функция описывает состояние макроскопического равновесного тела (подсистемы), помещенного в окружающую среду (другую подсистему) и составляющего с этой средой замкнутую систему. Сформулируем предварительные договоренности, на которые
Предполагается, что взаимодействием тела с окружающей средой в полном балансе энергий можно пренебречь. Тогда тело и окружающую среду можно считать квазинезависимыми (квазизамкнутыми) подсистемами, и полная энергия замкнутой системы определяется как
где Далее, пусть размер рассматриваемой подсистемы (тела) значительно меньше размера всей системы. Тогда число частиц
В макроскопических телах флуктуации энергии в состоянии равновесия малы ( Примечание: следует понимать, что, вообще говоря, для любой подсистемы мы не можем таким образом использовать среднее значение ее энергии, т.к. в качестве подсистемы можно выбрать и 1 молекулу, а тогда флуктуации энергии могут быть велики.
Нас интересует вероятность Это состояние среды можно описать фазовым объемом
при этом статистический вес макроскопического состояния равен
Фазовый объем
Фазовый объем, отвечающий макроскопическому состоянию окружающей среды, можно выразить через её энтропию (5.42):
Тогда можем записать
Подставляя в (6.4), получаем
Учтем, что тело составляет малую часть системы, т.е.
Ограничимся в разложении членом первого порядка по энергии
Тогда получаем
Здесь
Подставляя сюда (6.9), получаем:
Сравнивая теперь выражение (6.9) для вероятности макроскопического состояния тела с энергией
получаем выражение для плотности вероятности - функцию статистического распределения, или распределение Гиббса:
Формула (6.11) дает распределение вероятностей различных микроскопических состояний подсистемы, являющейся малой частью некоторой большой замкнутой системы. Это распределение было найдено Гиббсом в 1901 году. Используя распределение Гиббса, можно определить среднее значение физической величины, зависящей от координат и импульсов
6.2. Свободная энергия в распределении Гиббса.
Согласно (5.42) энтропия
где, напомним, Поскольку подсистема практически все время проводит в фазовом объеме
Поэтому можем записать
или, используя (6.11),
Средняя энергия – это как раз то, что понимают под энергией (внутренней энергией тела) подсистемы в термодинамике, поэтому знак усреднения опускаем, а для энтропии далее пишем Выражение (6.13) перепишем в виде
Вспоминая, что
т.е. нормировочная постоянная Тогда распределение Гиббса может быть записано в виде, в котором оно наиболее часто применяется
Поскольку свободная энергия
откуда
Эта формула является наиболее важной для термодинамических применений распределения Гиббса, поскольку устанавливает связь термодинамической величины
6.3. Уравнение состояния идеального газа. Уравнение состояния идеального газа можно вывести, используя соотношение (6.18), выражающее свободную энергию через распределение Гиббса. Поскольку в идеальном газе нет взаимодействия между молекулами, его полная энергия определяется лишь кинетической энергией хаотического движения молекул. Поэтому выражение (1.17) можно переписать в виде
Если в рассматриваемом объеме
Подставляя последнее соотношение в (6.19), имеем
Из курса термодинамики известно, что
Тогда
откуда
Т.о., мы получили уравнение состояния идеального газа – уравнение Менделеева-Клапейрона – из статистических соображений.
6.4. Распределения по кинетическим и потенциальным энергиям.
В классической физике полная энергия
где При таком подходе элемент фазового объема можно представить в виде произведения двух элементов:
где
т.е. представляется в виде произведения двух независимых сомножителей:
Это означает, что вероятность иметь определенные значения кинетической энергии никак не влияет на вероятность иметь одновременно какие-то значения потенциальной энергии. Поэтому вероятности Заметим, что такое разбиение на независимые распределения по кинетическим и потенциальным энергиям возможно лишь в классической физике. При квантовом рассмотрении задачи вероятности различных значений координат и импульсов оказываются связанными друг с другом соотношением неопределенностей.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 .
.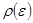 или
или  .
. . (6.1)
. (6.1) мы будем опираться, решая поставленную задачу.
мы будем опираться, решая поставленную задачу. ,
, энергия тела,
энергия тела,  энергия среды.
энергия среды. в полной системе и
в полной системе и  в малой подсистеме связаны соотношением:
в малой подсистеме связаны соотношением: .
. ). Поэтому под энергией
). Поэтому под энергией  можно понимать её среднее значение
можно понимать её среднее значение  . Однако в дальнейшем, если это не может привести к недоразумениям, знак усреднения
. Однако в дальнейшем, если это не может привести к недоразумениям, знак усреднения 
 такого состояния тела, при котором его энергия заключена в пределах от
такого состояния тела, при котором его энергия заключена в пределах от  , в то время как окружающая среда находится в равновесном макроскопическом состоянии со средней энергией
, в то время как окружающая среда находится в равновесном макроскопическом состоянии со средней энергией  . Напомним, что среда подавляющую часть времени находится в состоянии с энергией вблизи её среднего значения, поэтому условие нормировки может быть записано как
. Напомним, что среда подавляющую часть времени находится в состоянии с энергией вблизи её среднего значения, поэтому условие нормировки может быть записано как , (6.2)
, (6.2) . (6.3)
. (6.3) может быть распределена в окружающей подсистему среде. Так как тело и среда статистически независимы, то вероятность
может быть распределена в окружающей подсистему среде. Так как тело и среда статистически независимы, то вероятность 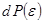 пропорциональна произведению фазового объема
пропорциональна произведению фазового объема  , описывающего состояние тела, и фазового объема, характеризующего макроскопическое состояние окружающей среды
, описывающего состояние тела, и фазового объема, характеризующего макроскопическое состояние окружающей среды  . (6.4)
. (6.4) . (6.5)
. (6.5) . (6.6)
. (6.6)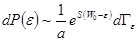 . (6.7)
. (6.7) . Используя это условие, разложим энтропию среды
. Используя это условие, разложим энтропию среды  в ряд Тейлора в окрестности точки
в ряд Тейлора в окрестности точки  :
: . (6.8)
. (6.8) ) и используем выражение для температуры, полученное нами ранее в разделе «Термодинамика»:
) и используем выражение для температуры, полученное нами ранее в разделе «Термодинамика»: .
. . (6.9)
. (6.9) включает все постоянные, не зависящие от энергии подсистемы (в частности,
включает все постоянные, не зависящие от энергии подсистемы (в частности, 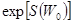 ,
,  и коэффициент пропорциональности). Постоянную
и коэффициент пропорциональности). Постоянную  .
. . (6.10)
. (6.10)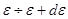 и выражение (5.29) (при
и выражение (5.29) (при  ):
): ,
, (6.11)
(6.11) :
: . (6.12)
. (6.12) подсистемы связана с её фазовым объемом уравнением
подсистемы связана с её фазовым объемом уравнением ,
, размерный коэффициент пропорциональности.
размерный коэффициент пропорциональности. , то выполняется условие нормировки (5.38):
, то выполняется условие нормировки (5.38): .
. ,
, . (6.13)
. (6.13) .
. . (6.14)
. (6.14) , получаем
, получаем , (6.15)
, (6.15) .
. (6.16)
(6.16) не зависит от скоростей и координат отдельных частиц подсистемы, то условие нормировки для функции (6.16) имеет вид
не зависит от скоростей и координат отдельных частиц подсистемы, то условие нормировки для функции (6.16) имеет вид , (6.17)
, (6.17) . (6.18)
. (6.18) . (6.19)
. (6.19) содержится
содержится  молекул, то
молекул, то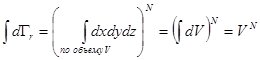 . (6.20)
. (6.20) . Записывая свободную энергию
. Записывая свободную энергию  .
. ,
, ;
;  , или
, или  . (6.21)
. (6.21) всегда может быть представлена как сумма кинетической
всегда может быть представлена как сумма кинетической 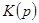 и потенциальной
и потенциальной  энергий:
энергий: , (6.22)
, (6.22) квадратичная функция импульсов (скоростей), а
квадратичная функция импульсов (скоростей), а  функция координат системы, вид которой, вообще говоря, зависит от закона взаимодействия атомов между собой и от внешнего поля (потенциальной энергии во внешнем поле), если таковое имеется.
функция координат системы, вид которой, вообще говоря, зависит от закона взаимодействия атомов между собой и от внешнего поля (потенциальной энергии во внешнем поле), если таковое имеется. , (6.23)
, (6.23) элемент фазового объема в пространстве импульсов (скоростей),
элемент фазового объема в пространстве импульсов (скоростей),  элемент фазового объема в пространстве координат. Тогда вероятность искомого события записывается в виде
элемент фазового объема в пространстве координат. Тогда вероятность искомого события записывается в виде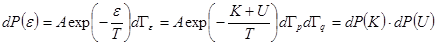 , (6.24)
, (6.24) ,
, .
.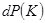 и
и  должны удовлетворять независимым условиям нормировки для определения постоянных
должны удовлетворять независимым условиям нормировки для определения постоянных  .
.