
|
|
Локальная и интегральная формулы Муавра-Лапласа.Методические указания к проведению лекционного занятия Тема № 7.7. Схема Бернулли План: 1. Формула Бернулли 2. Асимптотические формулы ü Формула Пуассона ü Локальная и интегральная формулы Муавра-Лапласа Формула Бернулли Рассмотрим стохастический эксперимент, который является последовательностью n независимых и однородных (одинаковых) испытаний, в результате каждого из которых может произойти событие А с вероятностью р и не произойти с вероятностью q=1-p. Например, имеется ящик с 30 деталями, которые проверяют на брак. Из ящика вынимают одну деталь. Если она оказалась бракованной, это означает, что произошло событие А={деталь бракованная}. Затем вынимают вторую деталь и выясняют, является ли она бракованной и т.д. Эти испытания являются независимыми, потому что тот факт, что первая деталь бракованная никак не влияет на брак любой другой детали. Найдем вероятность события, заключающегося в том, что в серии из n независимых испытаний событие А произойдет ровно k раз, Рn(x=k), где x – число наступлений события А. Для этого в ходе эксперимента должно произойти одно из событий А1·А2·А3·…·Аk· Здесь выписаны все возможные комбинации, в которых событие А произошло k раз и число их равно Аn-k+2·…·Аn)=Р(А1·А2·А3·…·Аk· Аn-k+1·Аn-k+2·…·Аn) Каждое из слагаемых в этой сумме равно рkqn-k, и всего таких слагаемых Значит, Рn(x=k)= Пример. Монету бросают 8 раз. Какова вероятность того, что: а) герб выпадет 5 раз; б) герб выпадет не более 2-х раз; в) герб выпадет более 2-х раз. Решение. Проводится серия из 8 независимых испытаний. Событие А, которое происходит или не происходит в каждом испытании, это А={выпадение герба при одном бросании}. Пусть x – число выпадений герба в серии из 8 независимых испытаний. а) Найдем вероятность Р8(x=5). По формуле Бернулли Р8(x=5)= Р8(x=5)= б) Найдем вероятность Р8(x в) Вероятность того, что герб выпадет более двух раз, удобно вычислить через противоположное событие {герб выпадет не более двух раз}. Р8(x Асимптотические формулы Применение формулы Бернулли при очень больших значениях n приводит к вычислению очень больших (n!) и очень малых чисел (рk, qn-k), что неудобно с вычислительной точки зрения, поэтому пользуются приближенными (асимптотическими) формулами. Формула Пуассона. Если проводится серия из n независимых, однородных испытаний, гдеn При решении задач можно пользоваться тем, что значения функции Рn(x=k)= Пример. При транспортировке и разгрузке керамической плитки повреждается 2,5%. Найти вероятность того, что в партии из 200 плиток поврежденными окажутся ровно 4 плитки. Решение. По условию задачи проводится 200 независимых однородных испытаний. Событие, которое наступает в одном испытании А={повреждение 1 плитки}. Так как n=200 Вероятность события, заключающегося в том, что событие появится не более k раз, вычисляется следующим образом: Рn(x Рn(x Значения функции Рn(x Пример. При транспортировке и разгрузке керамической плитки повреждается 2,5%. Найти вероятность того, что в партии из 200 плиток поврежденными окажутся не более 6 плиток. Решение. Требуется найти вероятность Р200(x Р200(x Локальная и интегральная формулы Муавра-Лапласа. Если проводится серия из n независимых, однородных испытаний, гдеn Функция Пример. Вероятность того, что в книге нет опечатки, равна 0,8. Найти вероятность того, что из 100 книг ровно 75 книг без опечаток. Решение. По условию задачи проводится 100 независимых однородных испытаний. Событие, которое наступает в одном испытании А={обнаружена опечатка в книге}. Так как n=100
Если нас интересует, что в серии из n независимых однородных испытаний, где n Рn(k1 Функция Пример. Вероятность того, что в книге нет опечатки, равна 0,8. Найти вероятность того, что из 100 книг не менее 75 книг без опечаток. Решение. Так как n=100
Контрольные вопросы: 1. В каких случаях применяется формула Бернулли? Приведите примеры. 2. В каких случаях применяется формула Пуассона? Приведите примеры. 3. В каких случаях применяются локальная и интегральная формулы Муавра-Лапласа? Приведите примеры.
Литература: 1. Высшая математика для экономистов: Учебник для вузов / Н.Ш. Кремер, Б.А. Путко, И.М. Тришин, М.Н.Фридман. Под ред. Н.Ш. Кремера. – М.: ЮНИТИ, 2005. – 471 с. 2. Общий курс высшей математики для экономистов: Учебник. / Под ред. В.И. Ермакова. –М.: ИНФРА-М, 2006. – 655 с. 3. Сборник задач по высшей математике для экономистов: Учебное пособие / Под ред.В.И. Ермакова. М.: ИНФРА-М, 2006. – 574 с. 4. Гмурман В. Е. Руководство к решению задач по теории вероятностей и магматической статистике. - М.: Высшая школа, 2005. – 400 с. 5. Гмурман. В.Е Теория вероятностей и математическая статистика. - М.: Высшая школа, 2005. 6. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Ч. 1, 2. – М.: Оникс 21 век: Мир и образование, 2005. – 304 с. Ч. 1; – 416 с. Ч. 2. 7. Математика в экономике: Учебник: В 2-х ч. / А.С. Солодовников, В.А. Бабайцев, А.В. Браилов, И.Г. Шандара. – М.: Финансы и статистика, 2006. 8. Шипачев В.С. Высшая математика: Учебник для студ. вузов – М.: Высшая школа, 2007. – 479 с.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 , …,
, …,  ·Аn-k+1·Аn-k+2·…·Аn.
·Аn-k+1·Аn-k+2·…·Аn. . Тогда, Рn(x=k)=Р(А1·А2·А3·…·Аk·
. Тогда, Рn(x=k)=Р(А1·А2·А3·…·Аk·  р5q8-5=
р5q8-5=  , q=1-p=
, q=1-p= 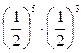 =
= 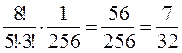 .
. 2). Герб выпадает не более 2 раз, если происходит одно из событий {герб не выпадет}, {герб выпадет один раз}, {герб выпадет два раза}. Таким образом, Р8(x
2). Герб выпадает не более 2 раз, если происходит одно из событий {герб не выпадет}, {герб выпадет один раз}, {герб выпадет два раза}. Таким образом, Р8(x 
 +
+  +
+ 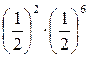 =
=  .
. 2)=1- Р8(x
2)=1- Р8(x  .
. , где λ=np.
, где λ=np. табулированы (см. табл. 1 приложения).
табулированы (см. табл. 1 приложения). . Вычислим λ=np=200·0,025=5. Р200(x=4)≈
. Вычислим λ=np=200·0,025=5. Р200(x=4)≈  =0,17547.
=0,17547. =
=  , т.е.
, т.е.
 табулированы (см. табл. 2 приложения).
табулированы (см. табл. 2 приложения). =0,76218.
=0,76218. ,где
,где  и
и  .
. также табулирована (см. табл. 3 приложения). Функция
также табулирована (см. табл. 3 приложения). Функция  , поэтому таблица ее значений составлена для x
, поэтому таблица ее значений составлена для x  .
. . Вычислим
. Вычислим 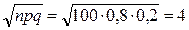 ,
,  . Тогда Р100(x=75)≈
. Тогда Р100(x=75)≈  = =
= =  ·0,1826=0,04565.
·0,1826=0,04565. 100событие А появится не менее k1 и не более k2 раз, с вероятностьюр>0,1в каждом испытании, то применяютинтегральную формулу Муавра-Лапласа:
100событие А появится не менее k1 и не более k2 раз, с вероятностьюр>0,1в каждом испытании, то применяютинтегральную формулу Муавра-Лапласа: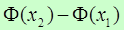 , где
, где  ,
,  и
и  .
. называется функцией Лапласа, ее значения табулированы (см. табл. 4 приложения). Функция
называется функцией Лапласа, ее значения табулированы (см. табл. 4 приложения). Функция  , поэтому таблица ее значений составлена для
, поэтому таблица ее значений составлена для  . Для больших значений аргумента с хорошей точностью можно считать, что
. Для больших значений аргумента с хорошей точностью можно считать, что  . Вычислим
. Вычислим 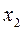 и
и  :
:  и
и  . Тогда Р100(75
. Тогда Р100(75  0,5+0,3944=0,8944.
0,5+0,3944=0,8944.