Интеграл от разрывной функции
(несобственный интеграл второго рода)
Определение 3.2. Пусть функция  непрерывна на промежутке непрерывна на промежутке  и имеет бесконечный разрыв при и имеет бесконечный разрыв при  . Если существует конечный предел . Если существует конечный предел 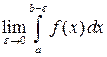 , где , где  , то его называют сходящимся несобственным интегралом второго рода и обозначают , то его называют сходящимся несобственным интегралом второго рода и обозначают  , т.е. , т.е.
 . (3.2) . (3.2)
Если же указанный предел не существует или он бесконечен, то говорят, что интеграл  расходится. расходится.

Аналогично, если функция  терпит бесконечный разрыв в точке терпит бесконечный разрыв в точке  , то полагают , то полагают
 . .
Если функция  терпит разрыв во внутренней точке терпит разрыв во внутренней точке  отрезка отрезка  , то несобственный интеграл второго рода определяется формулой , то несобственный интеграл второго рода определяется формулой
 . .
В этом случае интеграл слева называют сходящимся, если оба предела, стоящих справа существуют.
Пример 3.5. Вычислить несобственный интеграл или установить его расходимость:

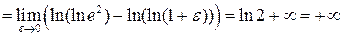 . .
Следовательно, данный интеграл расходится.
,
Пример 3.6. Вычислить несобственный интеграл или установить его расходимость:

 . .
Следовательно, данный интеграл сходится.
,
4. ДВОЙНОЙ ИНТЕГРАЛ
Двойной интеграл
Рассмотрим в плоскости  замкнутую область замкнутую область  . Область . Область  называется замкнутой, если она ограничена замкнутой линией, и точки, лежащие на границе, считаются принадлежащими области называется замкнутой, если она ограничена замкнутой линией, и точки, лежащие на границе, считаются принадлежащими области  . .
Пусть в области  задана непрерывная функция задана непрерывная функция  . .
Схема получения двойного интеграла
1) Разбиваем область  на на  «элементарных областей» «элементарных областей»  . .
2) Площадь области  обозначим обозначим  , а диаметр (наибольшее расстояние между двумя точками области) – через , а диаметр (наибольшее расстояние между двумя точками области) – через  . .
3) Возьмем произвольную точку 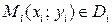 . .
4) Находим  , что равно объему тела (призма), площадь основания которого , что равно объему тела (призма), площадь основания которого  , а высота равна , а высота равна  . .
5) Составляем интегральную сумму
 . .

6) Обозначим через  длину наибольшего из диаметров «элементарных областей», т.е. длину наибольшего из диаметров «элементарных областей», т.е.  , ,  . Найдем предел интегральной суммы, когда . Найдем предел интегральной суммы, когда  так, что так, что  . Если предел существует и не зависит от способа разбиения области . Если предел существует и не зависит от способа разбиения области  на части, ни от выбора точек в них, то он называется двойным интегралом от функции на части, ни от выбора точек в них, то он называется двойным интегралом от функции  по области по области  . .
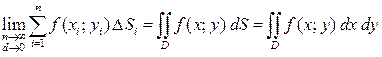 . .
Таким образом, двойным интегралом от  по замкнутой областью по замкнутой областью  называется предел интегральной суммы называется предел интегральной суммы  , когда число «элементарных областей» неограниченно возрастает, а длина наибольшего диаметра стремится к нулю: , когда число «элементарных областей» неограниченно возрастает, а длина наибольшего диаметра стремится к нулю:
 . (4.1) . (4.1)
 - интегрируемая функция в области - интегрируемая функция в области  ; ;
 - область интегрирования; - область интегрирования;
 и и  - переменные интегрирования; - переменные интегрирования;
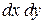 или или  - элемент площади. - элемент площади.
Для всякой ли функции  существует двойной интеграл? На этот вопрос отвечает следующая теорема, которую мы приведем без доказательства. существует двойной интеграл? На этот вопрос отвечает следующая теорема, которую мы приведем без доказательства.
Теорема 4.1 (достаточное условие интегрируемости функции).
Если функция  непрерывна в замкнутой области непрерывна в замкнутой области  ,то она интегрируема в этой области. ,то она интегрируема в этой области.
Замечание: далее будем рассматривать только функции, непрерывные в области интегрирования, хотя двойной интеграл может существовать не только для непрерывных функций.
Геометрический смысл двойного интеграла.
Двойной интеграл от неотрицательной функции (  ) численно равен объему тела, которое сверху ограничено поверхностью ) численно равен объему тела, которое сверху ограничено поверхностью  , снизу – замкнутой областью , снизу – замкнутой областью  плоскости плоскости  , с боков – цилиндрической поверхностью, образующая которой параллельна оси , с боков – цилиндрической поверхностью, образующая которой параллельна оси  , а направляющей служит граница , а направляющей служит граница  , т.е. , т.е.
 . .
Основные свойства двойного интеграла
Свойства двойного интеграла аналогичны свойствам определенного интеграла функции одной переменной на отрезке. Поэтому перечислим основные свойства двойного интеграла (без доказательства), считая подынтегральные функции интегрируемыми.
1.  , где , где  . .
2.  . .
3. Если область  разбить линией на две области разбить линией на две области  и и  такие, что такие, что  , а пересечение , а пересечение  , где , где  - линия, разделяющая - линия, разделяющая  и и  (см. рисунок), то (см. рисунок), то

4. Если в области  имеет место неравенство имеет место неравенство  , то и , то и
 . .
5. Если в области  функции функции 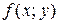 и и  удовлетворяют неравенству удовлетворяют неравенству  , то и , то и
 . .
6. Если  , , 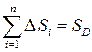 , то , то  , где , где  - площадь области интегрирования - площадь области интегрирования  . .
7. Если функция 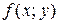 непрерывна в замкнутой области непрерывна в замкнутой области  , площадь которой , площадь которой  , то , то
 , ,
где  и и  - соответственно наименьшее и наибольшее значения подынтегральной функции в области - соответственно наименьшее и наибольшее значения подынтегральной функции в области  . .
8. Если функция 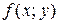 непрерывна в замкнутой области непрерывна в замкнутой области  , площадь которой , площадь которой  , то в этой области существует такая точка , то в этой области существует такая точка  , что , что
 . .
Величину 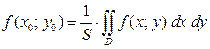 называют средним значением функции называют средним значением функции 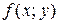 в области в области  . .
Вычисление двойного интеграла
В декартовых координатах
Покажем, что вычисление двойного интеграла сводится к последовательному вычислению двух определенных интегралов.
Пусть требуется вычислить двойной интеграл  , где функция , где функция  непрерывна в области непрерывна в области  . Тогда, двойной интеграл выражает объем цилиндрического тела, ограниченного сверху поверхностью . Тогда, двойной интеграл выражает объем цилиндрического тела, ограниченного сверху поверхностью  . Найдем этот объем, используя метод параллельных сечений. . Найдем этот объем, используя метод параллельных сечений.  , где , где 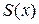 - площадь сечения плоскостью, перпендикулярной оси - площадь сечения плоскостью, перпендикулярной оси  , а , а  и и  - уравнения плоскостей, ограничивающих данное тело. - уравнения плоскостей, ограничивающих данное тело.

направлении оси  : любая прямая, параллельная оси : любая прямая, параллельная оси  , пересекает границу области не более чем в дух точках. , пересекает границу области не более чем в дух точках.
Построим сечение цилиндрического тела плоскостью, перпендикулярной оси  : : 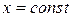 , где , где  . .
В сечении получаем криволинейную трапецию  , ограниченную линиями , ограниченную линиями  , где , где 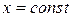 , ,  и и  . Площадь . Площадь 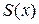 этой трапеции находим с помощью определенного интеграла: этой трапеции находим с помощью определенного интеграла:
 . .
Теперь, согласно методу параллельных сечений, искомый объем цилиндрического тела может быть найден так:
 . .
С другой стороны, объем цилиндрического тела определяется как двойной интеграл от функции  по области по области  . Следовательно, . Следовательно,
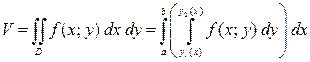 . .
Таким образом, для вычисления двойного интеграла функции  по области по области  используется следующая формула используется следующая формула
 . (4.2) . (4.2)
Правую часть (4.2) называют двукратным (или повторным) интегралом от функции 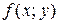 по области по области 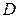 . Интеграл . Интеграл  называется внутренним интегралом. называется внутренним интегралом.
Для вычисления двукратного интеграла сначала берем внутренний интеграл, считая  постоянным, затем берем внешний интеграл, т.е. результат первого интегрирования интегрируем по постоянным, затем берем внешний интеграл, т.е. результат первого интегрирования интегрируем по  в пределах от в пределах от  до до  . .
Если область 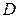 ограничена прямыми ограничена прямыми 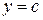 и и  ( (  ), кривыми ), кривыми  и и  , причем , причем  для всех для всех  , т.е. область , т.е. область 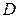 - правильная (стандартная) в направлении оси - правильная (стандартная) в направлении оси  , то, рассекая тело плоскостью , то, рассекая тело плоскостью  , аналогично получаем , аналогично получаем
 . (4.3) . (4.3)
Здесь при вычислении внутреннего интеграла, считаем  постоянным. постоянным.
Замечания.
1. Формулы (4.2) и (4.3) справедливы и в случае, когда  , ,  . .
2. Если область 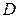 правильная в обоих направлениях, то двойной интеграл можно вычислять как и по формуле (4.2), так и по формуле (4.3). правильная в обоих направлениях, то двойной интеграл можно вычислять как и по формуле (4.2), так и по формуле (4.3).
3. Если область 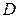 не является правильной ни «по не является правильной ни «по  », ни «по », ни «по  », то для сведения двойного интеграла к повторным ее следует разбить на части, правильные в направлении оси », то для сведения двойного интеграла к повторным ее следует разбить на части, правильные в направлении оси  или оси или оси  . .
4. Полезно помнить, что внешние пределы в двукратном интеграле всегда постоянны, а внутренние, как правило, переменные.
Пример 4.1. Вычислить  , если область , если область 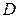 ограничена линиями: ограничена линиями:  . .
Решение. I способ.

II способ. Построенная область  является правильной в направлении оси является правильной в направлении оси  . Для вычисления двойного интеграла воспользуемся формулой (1.3): . Для вычисления двойного интеграла воспользуемся формулой (1.3):

 . .
,
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|


 непрерывна на промежутке
непрерывна на промежутке  и имеет бесконечный разрыв при
и имеет бесконечный разрыв при  . Если существует конечный предел
. Если существует конечный предел 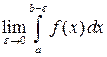 , где
, где  , то его называют сходящимся несобственным интегралом второго рода и обозначают
, то его называют сходящимся несобственным интегралом второго рода и обозначают  , т.е.
, т.е. . (3.2)
. (3.2)
 терпит бесконечный разрыв в точке
терпит бесконечный разрыв в точке  , то полагают
, то полагают .
. отрезка
отрезка  , то несобственный интеграл второго рода определяется формулой
, то несобственный интеграл второго рода определяется формулой .
.
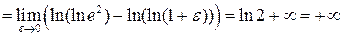 .
.
 .
. замкнутую область
замкнутую область  . Область
. Область  .
. «элементарных областей»
«элементарных областей»  .
. обозначим
обозначим  , а диаметр (наибольшее расстояние между двумя точками области) – через
, а диаметр (наибольшее расстояние между двумя точками области) – через  .
.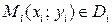 .
. , что равно объему тела (призма), площадь основания которого
, что равно объему тела (призма), площадь основания которого  .
. .
.
 длину наибольшего из диаметров «элементарных областей», т.е.
длину наибольшего из диаметров «элементарных областей», т.е.  ,
,  . Найдем предел интегральной суммы, когда
. Найдем предел интегральной суммы, когда  так, что
так, что  . Если предел существует и не зависит от способа разбиения области
. Если предел существует и не зависит от способа разбиения области 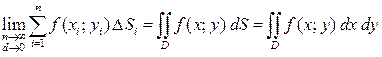 .
. , когда число «элементарных областей» неограниченно возрастает, а длина наибольшего диаметра стремится к нулю:
, когда число «элементарных областей» неограниченно возрастает, а длина наибольшего диаметра стремится к нулю: . (4.1)
. (4.1) и
и  - переменные интегрирования;
- переменные интегрирования;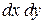 или
или  - элемент площади.
- элемент площади. ) численно равен объему тела, которое сверху ограничено поверхностью
) численно равен объему тела, которое сверху ограничено поверхностью  , а направляющей служит граница
, а направляющей служит граница  .
. , где
, где  .
. .
. и
и  такие, что
такие, что  , а пересечение
, а пересечение  , где
, где  - линия, разделяющая
- линия, разделяющая 
 .
.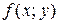 и
и  удовлетворяют неравенству
удовлетворяют неравенству  , то и
, то и .
. ,
, 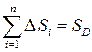 , то
, то  , где
, где  - площадь области интегрирования
- площадь области интегрирования  , то
, то ,
, и
и  - соответственно наименьшее и наибольшее значения подынтегральной функции в области
- соответственно наименьшее и наибольшее значения подынтегральной функции в области  , что
, что .
.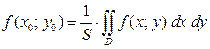 называют средним значением функции
называют средним значением функции  , где функция
, где функция  , где
, где 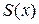 - площадь сечения плоскостью, перпендикулярной оси
- площадь сечения плоскостью, перпендикулярной оси  , а
, а 
 : любая прямая, параллельная оси
: любая прямая, параллельная оси 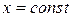 , где
, где  .
. , ограниченную линиями
, ограниченную линиями  и
и  . Площадь
. Площадь  .
. .
.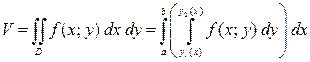 .
. . (4.2)
. (4.2)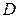 . Интеграл
. Интеграл  называется внутренним интегралом.
называется внутренним интегралом. до
до  .
.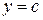 и
и  (
(  ), кривыми
), кривыми  и
и  , причем
, причем  для всех
для всех  , т.е. область
, т.е. область  , аналогично получаем
, аналогично получаем . (4.3)
. (4.3) ,
,  .
. , если область
, если область  .
.

 .
.