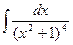|
|
Метод интегрирования по частям12 Формулой интегрирования по частям называют равенство
Применение этой формулы имеет целью заменить отыскание интеграла левой части отысканием интеграла правой, когда последний проще. К числу интегралов, вычисляемых интегрированием по частям, относятся, например, интегралы вида:
где P(x)- многочлен (в частности, степенная функция
Дадим два практических совета: 1. Если подынтегральная функция представляет собой произведение либо тригонометрической функции на алгебраическую, либо показательной на алгебраическую, то за u следует принимать алгебраическую функцию. 2. Если в подынтегральное выражение входит множителем либо одна из обратных тригонометрических функций
Пример 5. Вычислим следующие интегралы: 1. 4. 7. Решение. 1. Учитывая первый практический совет, положим u=x,
Замечание 8. Этот же интеграл можно взять другим способом. Если сравнить подынтегральную функцию и полученный ответ, то легко заметить, что оба они представляют собой произведение одной и той же функции Такой метод решения носит название метода неопределенных коэффициентов. Итак, решим этот пример методом неопределенных коэффициентов.
Продифференцировав обе части этого тождества, получаем: Так как производная от интеграла равна подынтегральной функции, то имеем:
Поскольку
в котором коэффициенты при одинаковых степенях x слева и справа должны быть обязательно одинаковыми. Отсюда имеем систему
решив которую, находим:
Таким образом,
что совпадает с ранее полученным ответом. 2. По аналогии с решением примера 1 получаем:
Левый столбик в скобках записывается из данного интеграла 3. Нередко формулу интегрирования но частям приходится применять последовательно несколько раз.
Этот интеграл также берется методом неопределенных коэффициентов: Остается продифференцировать левую и правую части этого тождества и сравнить коэффициенты при выражениях: Проделайте самостоятельно и сравните ответ с полученным ранее. Замечание 9. Интегралы, рассмотренные в примерах 1-3, представляют собой частные случаи интегралов вида:
в которых P(x)- многочлен, а a и b - постоянные величины. Также интегралы берутся либо способом последовательного интегрирования по частям, причем за u следует всегда принимать многочлен P(x) и интегрировать придется столько раз, какова степень многочлена, либо способом неопределенных коэффициентов как это показано в примерах 1, 3. 4. Учитывая второй практический совет, получим:
5. По аналогии с решением примера 26 имеем:
6. 7.
Иногда повторное применение формулы (1) интегрирования по частям приводит к уравнению искомого интеграла. Рассмотрим этот случай в следующем примере. 8. Обозначим искомый интеграл буквой I, получаем:
Перенося 9I в левую часть равенства и разделив на 10, находим
9. По аналогии с решением примера 8 имеем:
Отсюда получаем:
которая имеет вид:
Пример 6. Вычислим с помощью формулы (2) интеграл Решение. Применяя рекуррентную формулу (2) при n=3.
Задание 3. Самостоятельно выведите рекуррентные формулы для интегралов: 3.1 3.2 Указание. В первом интеграле положите Задание 4. Вычислить интегралы, применяя метод интегрирования по частям. 4.1. 4.4. 4.7. 4.10. 4.13.

12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
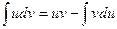 . (1)
. (1) ,
, ), f(x) - одна из следующих функций:
), f(x) - одна из следующих функций: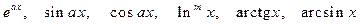 .
. и др., либо функция lnx, то за и. следует выбирать одну из указанных функций.
и др., либо функция lnx, то за и. следует выбирать одну из указанных функций.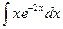 . 2.
. 2.  . 3.
. 3. 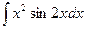 .
.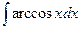 . 5.
. 5. 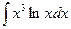 . 6.
. 6. 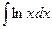 .
.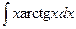 . 8.
. 8. 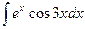 . 9.
. 9. 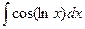 .
.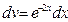 . Тогда
. Тогда 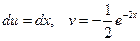 . Следовательно,по формуле (1) имеем:
. Следовательно,по формуле (1) имеем: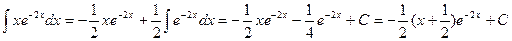 .
. на многочлен первой степени относительно x. Отсюда следует, что для интеграла
на многочлен первой степени относительно x. Отсюда следует, что для интеграла  , где A и B - пока еще неопределенные коэффициенты.
, где A и B - пока еще неопределенные коэффициенты.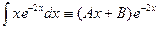 .
.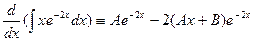 .
.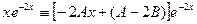 .
. , сократив на
, сократив на 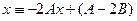 ,
,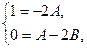
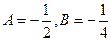 .
.
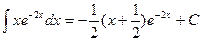 ,
,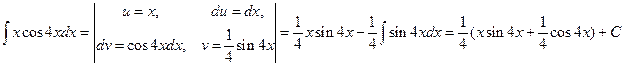 Примечание 3. Мы предлагаем такое оформление решения задачи методом интегрирования по частям, так как при такой записи легко запоминается формула (1).
Примечание 3. Мы предлагаем такое оформление решения задачи методом интегрирования по частям, так как при такой записи легко запоминается формула (1).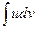 , а правый - из полученного
, а правый - из полученного 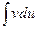 .
.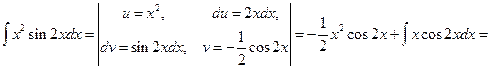
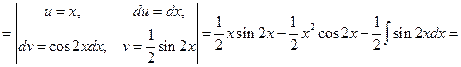
 .
.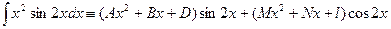 .
.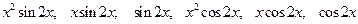 слева и справа.
слева и справа. ,
,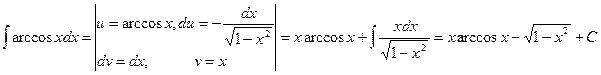 .Интеграл
.Интеграл  берется подстановкой
берется подстановкой  или подведением под знак дифференциала функции
или подведением под знак дифференциала функции 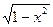 . Проделайте самостоятельно.
. Проделайте самостоятельно.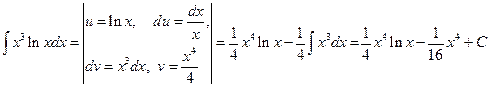 .
.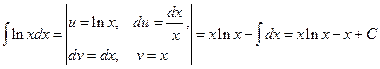 .
. .
.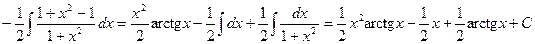 .
.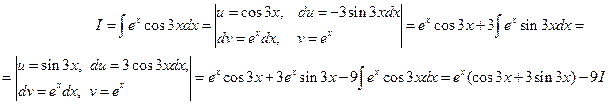
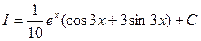 .
. . Но в случае при повторном интегрировании по частям следовало бы обязательно в качестве функции u выбрать показательную функцию.
. Но в случае при повторном интегрировании по частям следовало бы обязательно в качестве функции u выбрать показательную функцию.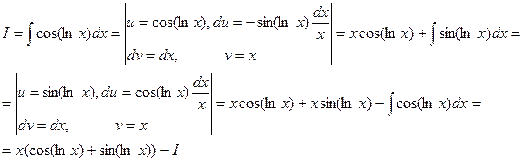
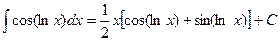 .
. ,
, . (2)
. (2)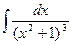 .
.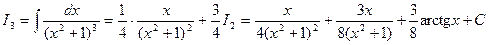 .
.
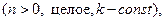

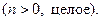
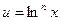 , а во втором представьте
, а во втором представьте 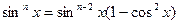 и положите
и положите  .
. 4.2.
4.2. 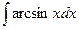 4.3.
4.3. 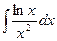
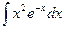 4.5.
4.5.  4.6.
4.6. 
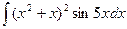 4.8.
4.8.  4.9.
4.9. 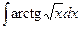
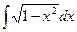 4.11.
4.11. 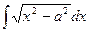 4.12.
4.12. 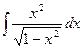
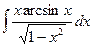 4.14.
4.14. 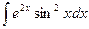 4.15.
4.15.