
|
|
Изображения периодических оригиналов.Операционное исчисление. Операционное исчисление является одной из важнейших глав математического анализа. Методы операционного исчисления используются в физике, механике, электротехнике и радиотехнике. Создан метод операционного исчисления во второй половине Х1Х века, но широкое распространение получил позднее, когда с помощью этого метода были получены важные результаты в электротехнике. Идея этого метода состоит в том, что надо найти функцию f(t) действительного переменного t, из некоторого уравнения, содержащего эту функцию под знаком производных и интегралов. Например, надо решить линейное дифференциальное уравнение
т.е. надо найти такую функцию x(t), которая удовлетворяла бы данному уравнению. Операционный метод решения этой задачи сводится к четырем шагам. 1. От искомой функции x(t) переходят к функции x(p), которая называется изображением функции x(t). 2. Над функцией x(p) производятся операции, соответствующие операциям над x(t), т.е. получают уравнение относительно x(p). Эти операции над x(p) оказываются более простыми, чем операции над x(t). 3. Полученное уравнение решают относительно x(p), что сводится к простым алгебраическим действиям. 4. От найденного изображения переходят к искомой функции x(t). Определение оператора Лапласа. Рассмотрим функцию f(t), удовлетворяющую следующим условиям. 1. f(t) определена при t ≥ 0. Если f(t) определена при t < 0, то предполагается, что f(t) ≡ 0.
Пусть p = a + i b – комплексное число с положительной действительной частью (a > 0). Оператором Лапласа называется несобственный интеграл
Можно показать, что при выполнении условий 1), 2), 3) этот интеграл сходится при Re p > s0 (a > s0 ). F(p) называется изображением функции f(t). Сама функция f(t) называется оригиналом.
Оператор Лапласа записывается в виде
Этот оператор ставит в соответствие функции действительного переменного f(t) функцию комплексного переменного F(p).
Единичная функция. Изображение функций sin ωt, cos ωt . Единичной функцией или функцией Хевисайда называется функция вида
0 x
1. L{k f(t)} = k L{f(t)}, 2. L{f1(t) + f2 (t)} = L{f1(t)} + L{f2(t)}. Теорема смещения. Если F(p)
Доказанная теорема позволяет расширить круг функций, для которых известны изображения.
Дифференцирование изображения. Теорема.
П р и м е р ы . 1. Известно, что
С учетом теоремы смещения имеем:
Известно, что
Аналогично,
Теорема запаздывания.
0, если t < τ, g(t) = f(t – τ), если t ≥ τ.
Если функция f(t) определяет течение некоторого процесса, то функция g(t) определяет тот же процесс, но с запаздыванием на величину τ. Эта функция с помощью единичной функции записывается в виде g(t) = 1(t - τ) f(t – τ). Теорема. Если τ > 0 и F(p )=> f(t), то e –p tF(p) => 1(t – τ) f(t – τ). Доказательство.
П р и м е р ы . Найти изображения функций. 1. 1/p e –ap => 1(t – a)
2.
0 τ t 3.
4.
f(t)
0 1 2 t
f(t) =2t 1(t) – 2t 1(t - 1) + (4 – 2t) 1(t -1) – (4 – 2t) 1(t – 2) = = 2t 1(t) – 4(t – 1) 1(t -1) + 2(t – 2) 1(t – 2). F(p)
6. f(t) = ½ sh at∙sin bt
7. Найти изображение.
8. Найти оригинал по изображению 9. Найти оригинал по изображению.
Теорема свертывания. Эта теорема позволяет в некоторых случаях находить оригиналы по изображению. Теорема. Если F1(p) => f1(t), F2(p) => f2(t), то
П р и м е р ы. 1. Найти оригинал по изображению. 2. Найти оригинал по изображению.
Теорема о дифференцировании оригинала. Теорема. Если F(p )=> f(t), то pF(p) - f(0 )=> f′(t). Находим далее изображение производной второго порядка. p (p F(p) – f(0)) - f′(0) => f′′(t), p2 F(p) – pf(0) - f′(0) => f′′(t) П р и м е р 1. Решить уравнение.
П р и м е р 2. Решить систему уравнений
Теорема об интегрировании изображения. Теорема. ПустьF(p) => f(t), тогда
П р и м е р . Найти изображение оригинала, используя теорему об интегрировании изображения.
Изображения периодических оригиналов. Пусть f(t) – периодическая функция с периодом Т. f(t + T) = f(t) для всех t > 0. Теорема. Изображение периодического оригиналаf(t) имеет вид
Доказательство. θ = t – T, t = θ + T, dt = dθ.
П р и м е р . Найти изображение оригинала f(t) с периодом Т. Построить график f(t).
f(t) = T = 4. 0, 3 ≤ t < 4.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 ,
,

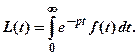


 1(t)Т.к.нас интересуеттолько интервал 0 ≤ t < ∞, то для
1(t)Т.к.нас интересуеттолько интервал 0 ≤ t < ∞, то для 1 нас эта функция – просто единица.
1 нас эта функция – просто единица.



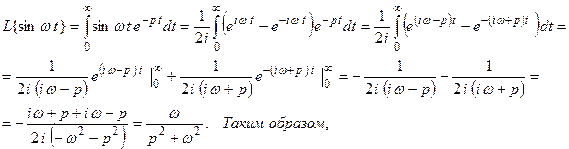

 Свойства оператора Лапласа.
Свойства оператора Лапласа. т.е. смещение аргумента на α соответствует умножению оригинала на е –αt.
т.е. смещение аргумента на α соответствует умножению оригинала на е –αt.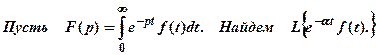


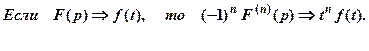






 Пусть имеем оригинал f(t), и пусть F(p) f(t). Рассмотрим некоторое τ > 0 и введем функцию
Пусть имеем оригинал f(t), и пусть F(p) f(t). Рассмотрим некоторое τ > 0 и введем функцию f(t)
f(t)  g(t)
g(t)





 t τ t
t τ t


 f(t) = 1(t – a), 1/ p =>1(t),
f(t) = 1(t – a), 1/ p =>1(t),
 1
1 








 A/p – A/p e –p τ => f(t)
A/p – A/p e –p τ => f(t)  f(t)
f(t)

 3
3






 2
2










 .
.
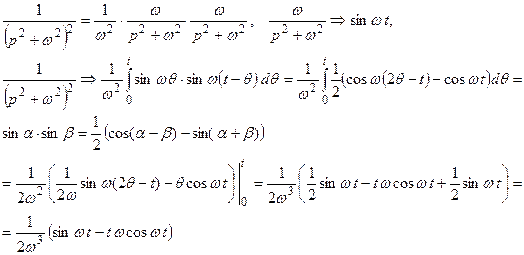












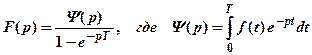


 2, 0 ≤ t < 3,
2, 0 ≤ t < 3, f(t)
f(t)











 0 3 4 7 8 t
0 3 4 7 8 t