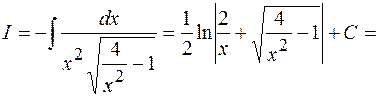Интегрирование некоторых иррациональных функций.
I.Рассмотрим здесь интегралы вида
 , ,
где  – числа, – числа,  . .
Чтобы вычислить этот интеграл, следует вычислить производную подкоренного выражения:

Затем в числителе подынтегральной функции следует выделить эту производную, поделив «уголком» числитель на полученную производную, то есть представить числитель в виде суммы двух слагаемых:

Тогда
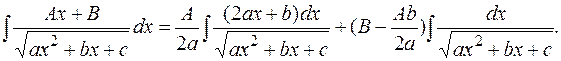 (9.1) (9.1)
Рассмотрим каждый из интегралов, стоящих в правой части (9.1), отдельно.
a) 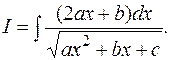 Положим Положим  . Тогда . Тогда 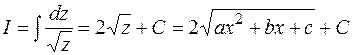 . .
b)  (9.2) (9.2)
Здесь в подкоренном выражении выделен полный квадрат. В результате правая часть равенства (9.2) приведена к табличному интегралу. Если 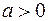 , это интеграл типа (3.16) из таблицы, если , это интеграл типа (3.16) из таблицы, если  – интеграл типа (3.14). – интеграл типа (3.14).
Пример 9.1. 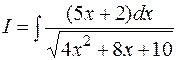 . Воспользуемся формулами . Воспользуемся формулами  , , 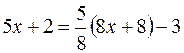 . Тогда . Тогда
 
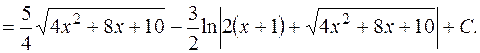
Пример 9.2.  . Воспользуемся формулами . Воспользуемся формулами  . Получим . Получим

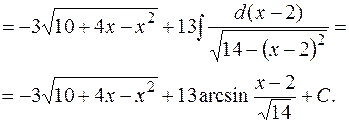
Пример 9.3. 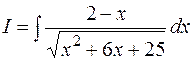 . Воспользуемся формулами . Воспользуемся формулами  . Получим . Получим


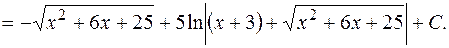
II.В разделе 7 мы показали, как интегрировать дробно-рациональные функции. В дальнейшем основным приемом интегрирования будет отыскание таких подстановок  (раздел 5), которые позволят избавиться от радикалов и приведут подынтегральное выражение к рациональному виду и тем самым позволят выразить исходный интеграл в виде функции аргумента (раздел 5), которые позволят избавиться от радикалов и приведут подынтегральное выражение к рациональному виду и тем самым позволят выразить исходный интеграл в виде функции аргумента  . Данный прием называется рационализацией подынтегрального выражения. Если при этом функция . Данный прием называется рационализацией подынтегрального выражения. Если при этом функция  такая, что существует обратная и можно выразить такая, что существует обратная и можно выразить  через через  с помощью элементарных функций, то интеграл представится и в виде функции аргумента с помощью элементарных функций, то интеграл представится и в виде функции аргумента  . Рассмотрим здесь тригонометрическую рационализацию для интегралов вида . Рассмотрим здесь тригонометрическую рационализацию для интегралов вида  и и  , где через , где через  обозначена дробно-рациональная функция двух аргументов. обозначена дробно-рациональная функция двух аргументов.
1). В интеграле  положим положим
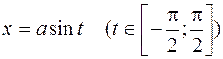 (9.3) (9.3)
и вычислим
 . .
Продифференцируем (9.3) и найдем 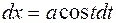 . Тогда исходный интеграл примет вид . Тогда исходный интеграл примет вид  .Вычисляя его, получим функцию, зависящую от .Вычисляя его, получим функцию, зависящую от  и тригонометрических функций аргумента и тригонометрических функций аргумента  .Чтобы вернуться к переменной .Чтобы вернуться к переменной  , следует из (9.3) выразить тригонометрическую функцию , следует из (9.3) выразить тригонометрическую функцию
 , (9.4) , (9.4)
откуда  . Затем в прямоугольном треугольнике отметим острый угол . Затем в прямоугольном треугольнике отметим острый угол  (рис. 1), противолежащий ему катет (рис. 1), противолежащий ему катет  и гипотенузу и гипотенузу  . Тогда по теореме Пифагора прилежащий катет равен . Тогда по теореме Пифагора прилежащий катет равен  . .

В этом треугольнике необходимые нам значения тригонометрических функций аргумента  выражаем как соотношения известных длин катетов и гипотенузы. выражаем как соотношения известных длин катетов и гипотенузы.
Замечание. Изложенный прием определения тригонометрических функций аргумента  применим лишь для применим лишь для  . Но в силу свойств тригонометрических функций все формулы справедливы и для других значений . Но в силу свойств тригонометрических функций все формулы справедливы и для других значений  . .
В примере 5.13 уже был применен прием рационализации для интеграла такого типа.
Пример 9.4 [6].  . Воспользуемся заменой (9.3), где . Воспользуемся заменой (9.3), где  , и формулами , и формулами 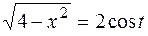 , , 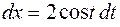 . Получим: . Получим:

Вернемся теперь к переменной  . Из (9.4) следует . Из (9.4) следует  и и  , а из треугольника, изображенного на рисунке 1, видно, что , а из треугольника, изображенного на рисунке 1, видно, что 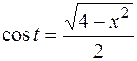 . Тогда . Тогда

2).В интеграле  положим положим
 (9.5) (9.5)
и вычислим
 . .
Продифференцируем (9.5) и найдем  . Тогда исходный интеграл примет вид . Тогда исходный интеграл примет вид 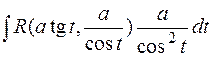 .Решая его, получим функцию, зависящую от .Решая его, получим функцию, зависящую от  и тригонометрических функций аргумента и тригонометрических функций аргумента  .Чтобы вернуться к переменной .Чтобы вернуться к переменной  , следует из (9.5) выразить тригонометрическую функцию , следует из (9.5) выразить тригонометрическую функцию
 , (9.6) , (9.6)
откуда 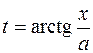 . Затем в прямоугольном треугольнике отметим острый угол . Затем в прямоугольном треугольнике отметим острый угол  (рис. 2), противолежащий ему катет (рис. 2), противолежащий ему катет  и прилежащий к нему катет и прилежащий к нему катет  . Тогда по теореме Пифагора гипотенуза равна . Тогда по теореме Пифагора гипотенуза равна 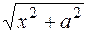 . .

Далее необходимые нам значения тригонометрических функций аргумента  выразим как соотношения известных длин катетов и гипотенузы в этом треугольнике. Приведем примеры применения приема рационализации для интеграла рассмотренного типа. выразим как соотношения известных длин катетов и гипотенузы в этом треугольнике. Приведем примеры применения приема рационализации для интеграла рассмотренного типа.
Пример 9.5.  . Воспользуемся заменой (9.5), где . Воспользуемся заменой (9.5), где 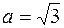 , и формулами , и формулами  , ,  . Получим . Получим
 . .
Вернемся теперь к переменной  . Для этого обратимся к рисунку 2 и выразим . Для этого обратимся к рисунку 2 и выразим  . Тогда . Тогда
 . .
3).В интеграле  положим положим
 (9.7) (9.7)
и вычислим
 . .
Продифференцируем (9.7) и найдем 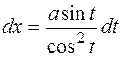 . Тогда исходный интеграл примет вид . Тогда исходный интеграл примет вид  .Решая его, получим функцию, зависящую от .Решая его, получим функцию, зависящую от  и тригонометрических функций аргумента и тригонометрических функций аргумента  .Чтобы вернуться к переменной .Чтобы вернуться к переменной  , следует из (9.7) выразить тригонометрическую функцию , следует из (9.7) выразить тригонометрическую функцию
 , (9.8) , (9.8)
откуда 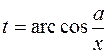 . Затем в прямоугольном треугольнике отметим острый угол . Затем в прямоугольном треугольнике отметим острый угол  (рис. 3), прилежащий к нему катет (рис. 3), прилежащий к нему катет  и гипотенузу и гипотенузу  . Тогда по теореме Пифагора противолежащий ему катет равен . Тогда по теореме Пифагора противолежащий ему катет равен  . .

Затем необходимые значения тригонометрических функций аргумента  выразим как соотношения известных длин катетов и гипотенузы в этом треугольнике. Приведем пример применения приема рационализации для интеграла третьего типа. выразим как соотношения известных длин катетов и гипотенузы в этом треугольнике. Приведем пример применения приема рационализации для интеграла третьего типа.
Пример 9.6.  . Введем новую функцию . Введем новую функцию
 (9.9) (9.9)
и воспользуемся формулами  , ,  . Получим: . Получим:

 . .
Теперь из (9.9) выразим  . Из прямоугольного треугольника, изображенного на рисунке 3, видно, что . Из прямоугольного треугольника, изображенного на рисунке 3, видно, что 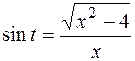 . Тогда . Тогда

III.Рационализацию интеграла вида
 , ,
где  означает рациональную функцию двух и более аргументов, осуществим с помощью замены означает рациональную функцию двух и более аргументов, осуществим с помощью замены
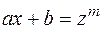 . (9.10) . (9.10)
Здесь показатель степени  равен такому числу, которое делится нацело на равен такому числу, которое делится нацело на  , другими словами , другими словами  есть наименьшее общее кратное для чисел есть наименьшее общее кратное для чисел  . Это позволит нам избавиться от радикалов. Продифференцируем равенство (9.10) . Это позволит нам избавиться от радикалов. Продифференцируем равенство (9.10)

и найдем 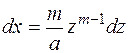 . Таким образом, все подынтегральное выражение будет сведено к рациональной функции одного аргумента . Таким образом, все подынтегральное выражение будет сведено к рациональной функции одного аргумента  . Ранее в примере 5.14 этот прием уже применялся. Приведем еще один пример. . Ранее в примере 5.14 этот прием уже применялся. Приведем еще один пример.
Пример 9.7.  . Сделаем замену . Сделаем замену 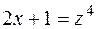 , продифференцируем это равенство , продифференцируем это равенство

и найдем 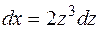 . Получим . Получим 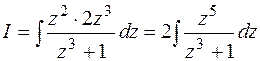 . Подынтегральная функция является неправильной рациональной дробью. Выделим её целую часть, поделив числитель на знаменатель. . Подынтегральная функция является неправильной рациональной дробью. Выделим её целую часть, поделив числитель на знаменатель.
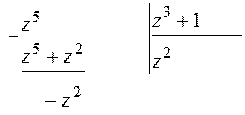
Тогда  . .
Затем вернемся к старой переменной по формуле  . Получим . Получим
 . .
Разные задачи.
Ниже приведены задачи, решение которых требует применения нескольких приемов интегрирования. Почти во всех этих задачах нужно сначала угадать выгодную замену переменной, которая привела бы в итоге к какой-нибудь стандартной формуле.
Пример 10.1.
 . Сделаем замену переменной . Сделаем замену переменной 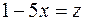 . Тогда . Тогда 
 . Снова введем новую переменную . Снова введем новую переменную  . Тогда . Тогда  . Возвращаясь к старой переменной по формуле . Возвращаясь к старой переменной по формуле  , получим , получим

Пример 10.2. 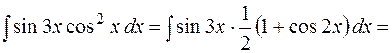
 

Пример 10.3.
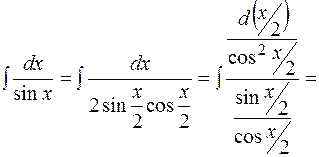 
Пример 10.4.  . .
Пример 10.5.  . Введем новую переменную . Введем новую переменную 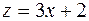 и получим и получим  (см. пример 6.2. из раздела 6 интегрирование по частям). Тогда (см. пример 6.2. из раздела 6 интегрирование по частям). Тогда

 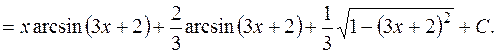
Пример 10.6.  . Введем новую переменную . Введем новую переменную  и найдем и найдем  . Получим . Получим 


Пример 10.7.  . Сделаем замену переменной . Сделаем замену переменной  . Тогда . Тогда  . Получим . Получим 
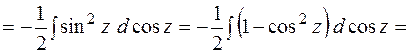

Пример 10.8. 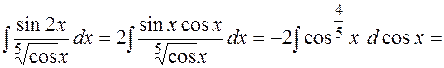

Пример 10.9.  . Введем новую переменную . Введем новую переменную  и найдем и найдем  . Тогда . Тогда 

 
Пример 10.10. 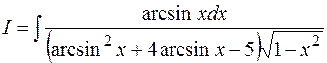 . Сделаем замену . Сделаем замену  и найдем и найдем  . Получим . Получим
 . Представим правильную дробь как сумму простейших дробей: . Представим правильную дробь как сумму простейших дробей:
 . .
Для нахождения неизвестных коэффициентов выпишем тождественное равенство исходного и вновь полученного числителей:
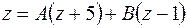 . .
Придадим переменной значение  . Тогда . Тогда  , откуда , откуда  . Затем при . Затем при  тождество примет вид: тождество примет вид:  , откуда , откуда  . Тогда . Тогда


Пример 10.11.  . Воспользуемся формулой интегрирования по частям. Положим . Воспользуемся формулой интегрирования по частям. Положим  . Найдем . Найдем  и и  . Тогда . Тогда 
Пример 10.12.  . Применим здесь формулу интегрирования по частям, полагая . Применим здесь формулу интегрирования по частям, полагая  . Тогда . Тогда  . Отсюда . Отсюда 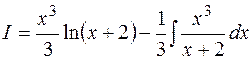 . Выделим в неправильной рациональной дроби целую часть делением числителя на знаменатель. . Выделим в неправильной рациональной дроби целую часть делением числителя на знаменатель.

Получим 
 . .
Пример 10.13. 
Здесь мы заметили, что  . .
Пример 10.14.  . Введем новую переменную . Введем новую переменную 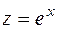 . Тогда . Тогда  . Получим . Получим  . Воспользуемся формулами . Воспользуемся формулами 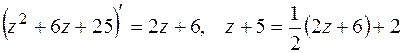 . Тогда . Тогда
 
 
Пример 10.15. 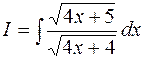 . Введем новую переменную . Введем новую переменную  . Найдем . Найдем  . Тогда . Тогда  , откуда , откуда 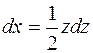 . Таким образом . Таким образом  . Получили интеграл, вычисленный ранее в примере 6.9. . Получили интеграл, вычисленный ранее в примере 6.9.


Пример 10.16.  . Сделаем замену переменной . Сделаем замену переменной 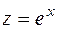 . Тогда . Тогда  и и  . Разложим правильную дробь в сумму простейших дробей: . Разложим правильную дробь в сумму простейших дробей:
 . .
Из тождественного равенства числителей  найдем неизвестные буквенные коэффициенты. найдем неизвестные буквенные коэффициенты.
При  тождество принимает вид тождество принимает вид  , откуда , откуда  . .
При  тождество принимает вид тождество принимает вид 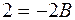 , откуда , откуда  . .
Отсюда 

Предложим другое решение, которое использует интеграл, взятый в примере 5.8.

Пример 10.17.  . Разложим подынтегральную функцию в сумму простейших дробей. . Разложим подынтегральную функцию в сумму простейших дробей.

Рассмотрим тождественное равенство исходного числителя и вновь полученного
 . .
Положим в нем последовательно  , а затем приравняем друг другу коэффициенты при , а затем приравняем друг другу коэффициенты при  . Тогда получим систему уравнений для нахождения неизвестных буквенных коэффициентов: . Тогда получим систему уравнений для нахождения неизвестных буквенных коэффициентов:
 . .
Решая ее, найдем  . Тогда . Тогда
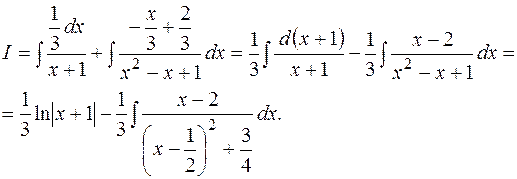
Вычислим отдельно  . Сделаем замену . Сделаем замену  . Найдем . Найдем  . Получим . Получим 
 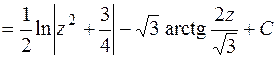 . Тогда . Тогда

Пример 10.18.  . Сделаем замену . Сделаем замену  и найдем и найдем  . Получим . Получим  . Подынтегральная функция является неправильной рациональной дробью. Выделим из нее целую часть. . Подынтегральная функция является неправильной рациональной дробью. Выделим из нее целую часть.
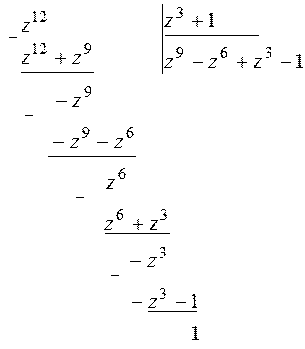
Тогда   . .
Последний интеграл взят в предыдущем примере 10.17. Воспользуемся этим результатом.

Затем вернемся к старой переменной  . .
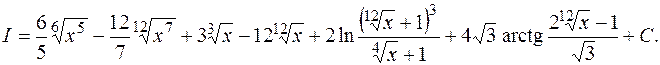 Пример 10.19. Пример 10.19.  . Сделаем замену переменной . Сделаем замену переменной  . При этом . При этом 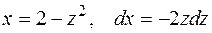 . Тогда . Тогда

Пример 10.20. Вычислить  . .
Пусть  . . 

При  : : 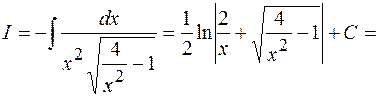

Рекомендуемая литература
1. Двайт Г.Б. Таблицы интегралов и другие математические формулы. М.: «Наука», 1964.
2. Выгодский М.Я. Справочник по высшей математике. М.: Изд-во АСТ Астрель, 2006.
3. Натансон И.П. Краткий курс высшей математики. СПб.: Изд-во «Лань», 2005.
4. Неопределенный интеграл. Методические указания к самостоятельному выполнению задания для студентов всех специальностей. Л.: ЛИСИ, 1989.
5. Письменный Д.Т. Конспект лекций по высшей математике. Ч. 1. М.: Айрис-пресс, 2006.
6. Берман Г.Н. Сборник задач по курсу математического анализа. М.: «Наука», 1985.
Оглавление
Введение3
1. Первообразная………………………………………………………….…..……3
2.Неопределенный интеграл……………………………………….………………4
3.Таблица неопределенных интегралов…………..………………….…………...6
4. Простейшие правила интегрирования…………………...……….…………11
5. Замена переменной в неопределенном интеграле…………..……….………17
6. Интегрирование по частям……….…………………………………………..20
7. Интегрирование дробно-рациональных функций………..….……….……..25
8. Интегрирование некоторых типов тригонометрических функций………...36
9. Интегрирование некоторых иррациональных функций……..…..…………40
10.Разные задачи………...………….............................................................42
Рекомендуемая литература…………………………………………………51
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Составители: Вера Борисовна Смирнова
Лидия Евсеевна Морозова
Редактор
Корректор
Компьютерная верстка
Подписано к печати 00.00.2005. Формат 60x84 1/16. Бум. Офсетная. Усл. печ. л. . Уч.-изд. л. . Тираж 2000 экз. Заказ . «С» . Санкт-Петербургский государственный архитектурно-строительный университет. 190005, Санкт-Петербург, 2-я Красноармейская, 4. Отпечатано на ризографе. 190005, Санкт-Петербург, 2-ая Красноармейская, 5.
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|


 ,
, – числа,
– числа,  .
.

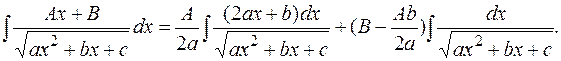 (9.1)
(9.1)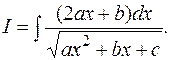 Положим
Положим  . Тогда
. Тогда 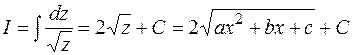 .
. (9.2)
(9.2)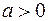 , это интеграл типа (3.16) из таблицы, если
, это интеграл типа (3.16) из таблицы, если  – интеграл типа (3.14).
– интеграл типа (3.14).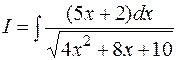 . Воспользуемся формулами
. Воспользуемся формулами  ,
, 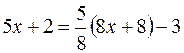 . Тогда
. Тогда

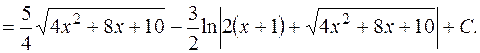
 . Воспользуемся формулами
. Воспользуемся формулами  . Получим
. Получим
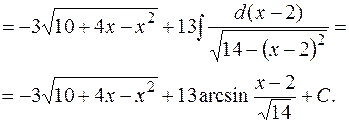
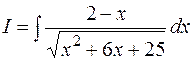 . Воспользуемся формулами
. Воспользуемся формулами  . Получим
. Получим

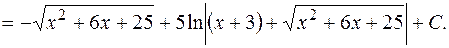
 (раздел 5), которые позволят избавиться от радикалов и приведут подынтегральное выражение к рациональному виду и тем самым позволят выразить исходный интеграл в виде функции аргумента
(раздел 5), которые позволят избавиться от радикалов и приведут подынтегральное выражение к рациональному виду и тем самым позволят выразить исходный интеграл в виде функции аргумента  . Данный прием называется рационализацией подынтегрального выражения. Если при этом функция
. Данный прием называется рационализацией подынтегрального выражения. Если при этом функция  с помощью элементарных функций, то интеграл представится и в виде функции аргумента
с помощью элементарных функций, то интеграл представится и в виде функции аргумента  и
и  , где через
, где через  обозначена дробно-рациональная функция двух аргументов.
обозначена дробно-рациональная функция двух аргументов. положим
положим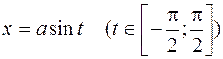 (9.3)
(9.3) .
.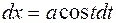 . Тогда исходный интеграл примет вид
. Тогда исходный интеграл примет вид  .Вычисляя его, получим функцию, зависящую от
.Вычисляя его, получим функцию, зависящую от  , (9.4)
, (9.4) . Затем в прямоугольном треугольнике отметим острый угол
. Затем в прямоугольном треугольнике отметим острый угол  . Тогда по теореме Пифагора прилежащий катет равен
. Тогда по теореме Пифагора прилежащий катет равен  .
.
 . Но в силу свойств тригонометрических функций все формулы справедливы и для других значений
. Но в силу свойств тригонометрических функций все формулы справедливы и для других значений  . Воспользуемся заменой (9.3), где
. Воспользуемся заменой (9.3), где  , и формулами
, и формулами 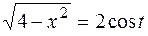 ,
, 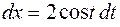 . Получим:
. Получим:
 и
и  , а из треугольника, изображенного на рисунке 1, видно, что
, а из треугольника, изображенного на рисунке 1, видно, что 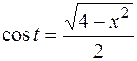 . Тогда
. Тогда
 положим
положим (9.5)
(9.5) .
. . Тогда исходный интеграл примет вид
. Тогда исходный интеграл примет вид 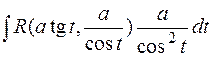 .Решая его, получим функцию, зависящую от
.Решая его, получим функцию, зависящую от  , (9.6)
, (9.6)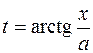 . Затем в прямоугольном треугольнике отметим острый угол
. Затем в прямоугольном треугольнике отметим острый угол 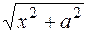 .
.
 . Воспользуемся заменой (9.5), где
. Воспользуемся заменой (9.5), где 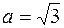 , и формулами
, и формулами  ,
,  . Получим
. Получим .
. . Тогда
. Тогда .
. положим
положим (9.7)
(9.7) .
.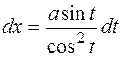 . Тогда исходный интеграл примет вид
. Тогда исходный интеграл примет вид  .Решая его, получим функцию, зависящую от
.Решая его, получим функцию, зависящую от  , (9.8)
, (9.8)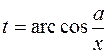 . Затем в прямоугольном треугольнике отметим острый угол
. Затем в прямоугольном треугольнике отметим острый угол  .
.
 . Введем новую функцию
. Введем новую функцию (9.9)
(9.9) ,
,  . Получим:
. Получим:
 .
. . Из прямоугольного треугольника, изображенного на рисунке 3, видно, что
. Из прямоугольного треугольника, изображенного на рисунке 3, видно, что 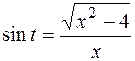 . Тогда
. Тогда
 ,
,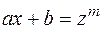 . (9.10)
. (9.10) равен такому числу, которое делится нацело на
равен такому числу, которое делится нацело на  , другими словами
, другими словами 
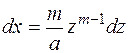 . Таким образом, все подынтегральное выражение будет сведено к рациональной функции одного аргумента
. Таким образом, все подынтегральное выражение будет сведено к рациональной функции одного аргумента  . Ранее в примере 5.14 этот прием уже применялся. Приведем еще один пример.
. Ранее в примере 5.14 этот прием уже применялся. Приведем еще один пример. . Сделаем замену
. Сделаем замену 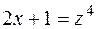 , продифференцируем это равенство
, продифференцируем это равенство
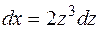 . Получим
. Получим 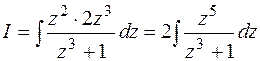 . Подынтегральная функция является неправильной рациональной дробью. Выделим её целую часть, поделив числитель на знаменатель.
. Подынтегральная функция является неправильной рациональной дробью. Выделим её целую часть, поделив числитель на знаменатель.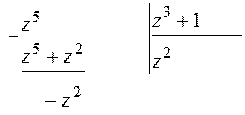
 .
. . Получим
. Получим .
. . Сделаем замену переменной
. Сделаем замену переменной 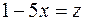 . Тогда
. Тогда 
 . Снова введем новую переменную
. Снова введем новую переменную  . Тогда
. Тогда  . Возвращаясь к старой переменной по формуле
. Возвращаясь к старой переменной по формуле  , получим
, получим
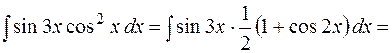



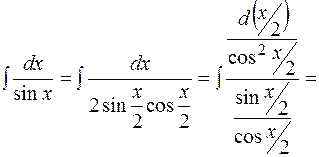

 .
. . Введем новую переменную
. Введем новую переменную 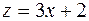 и получим
и получим  (см. пример 6.2. из раздела 6 интегрирование по частям). Тогда
(см. пример 6.2. из раздела 6 интегрирование по частям). Тогда

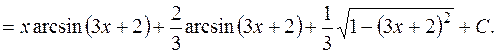
 . Введем новую переменную
. Введем новую переменную  и найдем
и найдем  . Получим
. Получим 


 . Сделаем замену переменной
. Сделаем замену переменной  . Тогда
. Тогда  . Получим
. Получим 
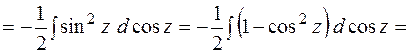

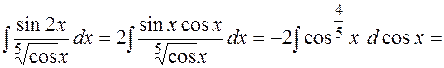

 . Введем новую переменную
. Введем новую переменную  и найдем
и найдем  . Тогда
. Тогда 


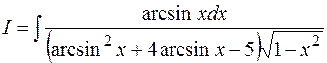 . Сделаем замену
. Сделаем замену  и найдем
и найдем  . Получим
. Получим . Представим правильную дробь как сумму простейших дробей:
. Представим правильную дробь как сумму простейших дробей: .
.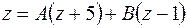 .
. . Тогда
. Тогда  , откуда
, откуда  . Затем при
. Затем при  тождество примет вид:
тождество примет вид:  , откуда
, откуда  . Тогда
. Тогда

 . Воспользуемся формулой интегрирования по частям. Положим
. Воспользуемся формулой интегрирования по частям. Положим  . Найдем
. Найдем  и
и  . Тогда
. Тогда 
 . Применим здесь формулу интегрирования по частям, полагая
. Применим здесь формулу интегрирования по частям, полагая  . Тогда
. Тогда  . Отсюда
. Отсюда 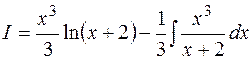 . Выделим в неправильной рациональной дроби целую часть делением числителя на знаменатель.
. Выделим в неправильной рациональной дроби целую часть делением числителя на знаменатель.

 .
.
 .
. . Введем новую переменную
. Введем новую переменную 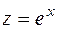 . Тогда
. Тогда  . Получим
. Получим  . Воспользуемся формулами
. Воспользуемся формулами 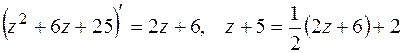 . Тогда
. Тогда



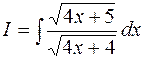 . Введем новую переменную
. Введем новую переменную  . Найдем
. Найдем  . Тогда
. Тогда  , откуда
, откуда 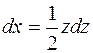 . Таким образом
. Таким образом  . Получили интеграл, вычисленный ранее в примере 6.9.
. Получили интеграл, вычисленный ранее в примере 6.9.

 . Сделаем замену переменной
. Сделаем замену переменной  . Разложим правильную дробь в сумму простейших дробей:
. Разложим правильную дробь в сумму простейших дробей: .
. найдем неизвестные буквенные коэффициенты.
найдем неизвестные буквенные коэффициенты. тождество принимает вид
тождество принимает вид  , откуда
, откуда  .
. тождество принимает вид
тождество принимает вид 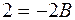 , откуда
, откуда  .
.


 . Разложим подынтегральную функцию в сумму простейших дробей.
. Разложим подынтегральную функцию в сумму простейших дробей.
 .
. , а затем приравняем друг другу коэффициенты при
, а затем приравняем друг другу коэффициенты при  . Тогда получим систему уравнений для нахождения неизвестных буквенных коэффициентов:
. Тогда получим систему уравнений для нахождения неизвестных буквенных коэффициентов: .
. . Тогда
. Тогда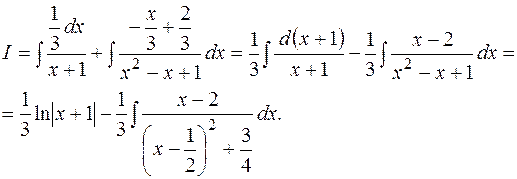
 . Сделаем замену
. Сделаем замену  . Найдем
. Найдем  . Получим
. Получим 

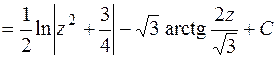 . Тогда
. Тогда
 . Сделаем замену
. Сделаем замену  и найдем
и найдем  . Получим
. Получим  . Подынтегральная функция является неправильной рациональной дробью. Выделим из нее целую часть.
. Подынтегральная функция является неправильной рациональной дробью. Выделим из нее целую часть.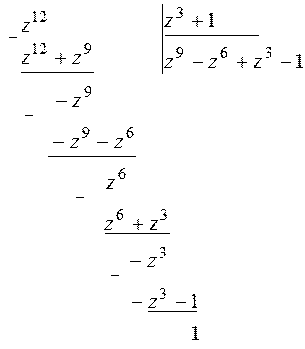

 .
.
 .
.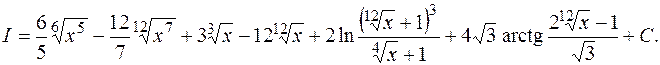 Пример 10.19.
Пример 10.19.  . Сделаем замену переменной
. Сделаем замену переменной  . При этом
. При этом 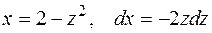 . Тогда
. Тогда
 .
. .
. 

 :
: