
|
|
Интегрирование дробно-рациональных функций.
Определение 3. Дробно-рациональной функцией (или рациональной дробью) будем называть частное от деления двух многочленов. Общий вид рациональной дроби таков где Если
где A, B, D, a, p, q – действительные числа, а трехчлен В целом классификацию рациональных дробей можно представить следующим образом.
Интегралы от рациональных дробей всегда являются берущимися. Покажем это, двигаясь по приведённой здесь схеме, поднимаясь с нижнего уровня на верхний уровень.
Интегрирование простейших дробей.
1. Интеграл типа (I) берется с использованием формулы (3.3) таблицы 1 и линейной замены.
2. Интеграл типа (II) берется с использованием формулы (3.2) таблицы 1 и линейной замены.
3. Рассмотрим интеграл типа (III) Чтобы вычислить интеграл
Далее представим числитель как сумму двух слагаемых:
т.е. “выделим” в числителе производную знаменателя. Теперь
Вычислим каждый из интегралов, стоящих в правой части (7.1), отдельно: · ·
Таким образом,
Заметим, что Формула (7.2) сложна для запоминания. Как правило, ею не пользуются, а непосредственно применяют к конкретному интегралу изложенный здесь метод. Приведём примеры. Пример 7.1. Пример 7.2.
Пример 7.3.
4. Для интеграла типа (IV)
Интегрирование правильных дробей общего вида.
Рассмотрим правильную дробь Представление правильной дроби в виде суммы простейших дробей осуществляется по следующему правилу. 1) Знаменатель
где 2) Следует построить “общий вид” представления с неопределёнными пока коэффициентами. При этом каждому множителю
а каждому множителю
где коэффициенты 3) Следует определить коэффициенты представления, полученного в пункте 2, исходя из тождественного равенства правильной дроби и суммы простейших дробей, полученной в пункте 2. Покажем на конкретных примерах, как пользоваться данным правилом. Пример 7.4. Применим сформулированное выше правило. 1) Разложим знаменатель дроби, стоящей под знаком интеграла, на множители:
2) Построим для дроби, стоящей под знаком интеграла, представление в виде суммы простейших дробей с неизвестными пока коэффициентами
Множитель 3) Приведём правую часть равенства (7.5) к общему знаменателю. Получим
Равенство (7.6) должно выполняться при всех значениях
при всех значениях
Система (7.8) имеет решение:
Замечание. Если коэффициенты
Таким образом, коэффициенты найдены верно. Итак, мы получили тождество
Тогда
Пример 7.5. Представим дробь, стоящую под знаком интеграла, в виде суммы простейших дробей. Так как оба множителя, стоящих в знаменателе, имеют степень 1, представление будет иметь вид
Заметим, что если в знаменателе стоит квадратный трёхчлен Приводим правую часть (7.9) к общему знаменателю. Тогда
откуда следует
Нужно определить три коэффициента
Система (7.11) имеет решение:
Проверим полученный результат.
Получено тождество
Следовательно,
Отдельно вычислим
Итак,
Пример 7.6. Разлагаем знаменатель на множители:
Выписываем общий вид представления дроби в виде суммы простейших дробей и сразу же приводим сумму дробей к общему знаменателю:
Составляем равенство числителей двух равных дробей с одинаковыми знаменателями:
Выбираем удобные значения
Решаем систему (7.13):
Проверим полученные значения.
Таким образом,
Интегрирование неправильных дробей.
Чтобы проинтегрировать неправильную дробь
где степень многочлена
Здесь Представление (7.14) иногда легко угадать (если Приведём примеры. Пример 7.7.
Пример 7.8.
Пример 7.9.
Вычислим отдельно
Окончательно,
Пример 7.10.
Вычислим отдельно
Подставим в полученное тождество последовательно значения переменной
Получим Окончательно,

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 ,
, – многочлен степени
– многочлен степени  , а
, а  – многочлен степени
– многочлен степени  .
. , то рациональная дробь называется правильной, если
, то рациональная дробь называется правильной, если  , то рациональная дробь называется неправильной. Из общей совокупности правильных дробей выделяются четыре специальных типа дробей, называемых простейшими. Простейшие дроби имеют вид
, то рациональная дробь называется неправильной. Из общей совокупности правильных дробей выделяются четыре специальных типа дробей, называемых простейшими. Простейшие дроби имеют вид
 не имеет действительных корней (
не имеет действительных корней (  ), т.е. не раскладывается на множители первой степени.
), т.е. не раскладывается на множители первой степени.
 .
.
 . ( Здесь
. ( Здесь  .)
.) , где
, где  .
. , найдём сначала производную знаменателя подынтегральной функции:
, найдём сначала производную знаменателя подынтегральной функции: .
. ,
, можно представить как сумму двух слагаемых:
можно представить как сумму двух слагаемых: . (7.1)
. (7.1) ,
,
 .
. . (7.2)
. (7.2) всегда можно представить как сумму квадратов в силу того, что
всегда можно представить как сумму квадратов в силу того, что  .
. .
. . Найдем производную знаменателя
. Найдем производную знаменателя  . Выделим эту производную в числителе
. Выделим эту производную в числителе  . Тогда
. Тогда
 .
. . Воспользуемся формулами
. Воспользуемся формулами . Тогда
. Тогда

 , где
, где  ,
, 
 , которая не является простейшей дробью. Чтобы проинтегрировать такую функцию, её нужно представить в виде суммы простейших дробей.
, которая не является простейшей дробью. Чтобы проинтегрировать такую функцию, её нужно представить в виде суммы простейших дробей. и
и  ,
, , а
, а  при условии
при условии  , (7.3)
, (7.3) , (7.4)
, (7.4)

 пока неизвестны и представлены буквами. В суммах (7.3) и (7.4) должны обязательно присутствовать все перечисленные выше слагаемые (
пока неизвестны и представлены буквами. В суммах (7.3) и (7.4) должны обязательно присутствовать все перечисленные выше слагаемые (  слагаемых в сумме (7.3) и
слагаемых в сумме (7.3) и  слагаемых в (7.4)) . Общий вид представления содержит в себе все суммы (7.3) и (7.4).
слагаемых в (7.4)) . Общий вид представления содержит в себе все суммы (7.3) и (7.4). .
. .
. . (7.5)
. (7.5) имеет степень 1, и ему соответствует в сумме одно слагаемое, множитель
имеет степень 1, и ему соответствует в сумме одно слагаемое, множитель  имеет степень 2, и ему в сумме соответствуют два слагаемых.
имеет степень 2, и ему в сумме соответствуют два слагаемых. . (7.6)
. (7.6) . Поскольку знаменатели дробей, стоящих в левой и правой частях (7.6), одинаковы, числители этих дробей должны быть тождественно равными. Таким образом,
. Поскольку знаменатели дробей, стоящих в левой и правой частях (7.6), одинаковы, числители этих дробей должны быть тождественно равными. Таким образом, (7.7)
(7.7)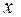 . Чтобы определить
. Чтобы определить  и
и  , подставим в (7.7) три каких-либо значения
, подставим в (7.7) три каких-либо значения 
 и
и  . Последовательно подставляя эти значения
. Последовательно подставляя эти значения  (7.8)
(7.8) ;
;  ;
;  .
. ,
,  найдены верно, то слева и справа в (7.7) стоят одинаковые многочлены. Следовательно, их коэффициенты при одинаковых степенях должны быть равны. Установим это:
найдены верно, то слева и справа в (7.7) стоят одинаковые многочлены. Следовательно, их коэффициенты при одинаковых степенях должны быть равны. Установим это:
 .
. .
. .
. . (7.9)
. (7.9) , то в числителе обязательно должен стоять многочлен первой степени
, то в числителе обязательно должен стоять многочлен первой степени  .
. ,
, . (7.10)
. (7.10) . Используем удобные значения:
. Используем удобные значения: 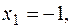

 . Подставим их последовательно в (7.10). Получим
. Подставим их последовательно в (7.10). Получим . (7.11)
. (7.11) ;
;  .
.
 .
. .
. , используя формулы
, используя формулы .
.
 .
. .
. .
. .
.
 .
. . (7.12)
. (7.12)
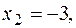
 ,
,  и составляем систему уравнений для определения четырёх коэффициентов:
и составляем систему уравнений для определения четырёх коэффициентов:  .
. . (7.13)
. (7.13)
 ,
,  .
.

 .
. , где
, где  в виде
в виде , (7.14)
, (7.14) меньше, чем степень многочлена
меньше, чем степень многочлена  является частным, а многочлен
является частным, а многочлен  является остатком. Затем равенство (7.14) следует почленно поделить на
является остатком. Затем равенство (7.14) следует почленно поделить на  .
. – правильная дробь.
– правильная дробь. имеют достаточно простой вид), но, как правило, оно получается в результате деления
имеют достаточно простой вид), но, как правило, оно получается в результате деления 
 .
.
 .
. Подынтегральная функция является неправильной рациональной дробью. Разделим числитель этой дроби на знаменатель с остатком.
Подынтегральная функция является неправильной рациональной дробью. Разделим числитель этой дроби на знаменатель с остатком.
 .
.
 .
. .
. . Поделим числитель на знаменатель с остатком.
. Поделим числитель на знаменатель с остатком.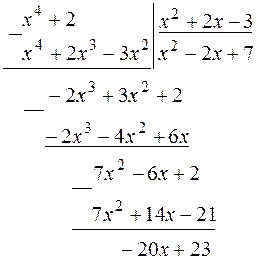
 .
. . Разложим правильную дробь на простейшие дроби.
. Разложим правильную дробь на простейшие дроби. .
. 
 .
. . Тогда
. Тогда
 .
. .
.