
|
|
Решение задач на интегрирование функций в среде Mathcad.Постановка задачи. Многие инженерные задачи, задачи физики, геометрии и многих других областей человеческой деятельности приводят к необходимости вычислять определенный интеграл вида
где F(x) данная функция, непрерывная на отрезке [a; b]. Если функция F(x) задана формулой, то определенный интеграл вычисляется по формуле Ньютона-Лейбница:
Также для вычисления определенного интеграла применяют приближенные формулы. Для приближенного вычисления интеграла (1.1) существует много численных методов, из которых рассмотрим три основных: 1) метод прямоугольников; 2) метод трапеций; 3) метод Симпсона. При вычислении интеграла следует помнить, каков геометрический смысл определенного интеграла. Если Таким образом, вычисление интеграла равносильно вычислению площади криволинейной трапеции.
Рис. 1.1. Численные методы, применяемые при вычислении интеграла
Метод прямоугольников. Разделим отрезок [a; b] на n равных частей, т.е. на n элементарных отрезков. Длина каждого элементарного отрезка xn-1=a+(n-1)×h; xn=b. Эти числа будем называть узлами. Вычислим значения функции F(x) в узлах, обозначим их y0, y1, y2, ... , yn. Cтало быть, y0=f(a), y1=f(x1), y2=f(x2), ... , yn=f(b). Числа y0, y1, y2, ... , yn являются ординатами точек графика функции, соответствующих абсциссам x0, x1, x2, ... , xn (рис. 1.2). Из рис. 1.2 следует, что площадь криволинейной трапеции приближенно заменяется площадью многоугольника, составленного из n прямоугольников. Таким образом, вычисление определенного интеграла сводится к нахождению суммы n элементарных прямоугольников.
Формула (1.3) называется формулой левых прямоугольников, (1.4) - формулой правых прямоугольников, (1.5) - формулой средних прямоугольников.
Рис. 1.2.
Метод трапеций. Формула трапеций:
Формула (1.6) означает, что площадь криволинейной трапеции заменяется площадью многоугольника, составленного из n трапеций (рис. 1.3); при этом кривая заменяется вписанной в нее ломаной.
Рис 1.3. Метод Симпсона. Геометрически иллюстрация формулы Симпсона состоит в том, что на каждом из сдвоенных частичных отрезков заменяем дугу данной кривой дугой графика квадратного трехчлена. Разобьем отрезок интегрирования [a; b] на 2×n равных частей длины
(1.7) Каждая из формул (1.3) – (1.7), как правило, дает результат тем точнее, чем больше n. Из всех приведенных формул наиболее точной является формула Симпсона, наименее точной - формулы прямоугольников.
Особенности интегрирования в MATHCAD Чтобы вычислить определенный интеграл, следует напечатать его обычную математическую форму в документе. Делается это с помощью панели Calculus (Вычисления) нажатием кнопки со значком интеграла или вводом с клавиатуры сочетания клавиш <Shift>+<7> (или символа "&"). Появится символ интеграла с несколькими местозаполнителями, в которые нужно ввести нижний и верхний интервалы интегрирования, подынтегральную функцию и переменную интегрирования. Можно вычислять интегралы с одним или обоими бесконечными пределами. Для этого на месте соответствующего предела введите символ бесконечности, воспользовавшись, например, той же самой панелью Calculus (Вычисления). Чтобы ввести минус бесконечность, добавьте знак минус к символу бесконечности, как к обычному числу. Чтобы получить результат интегрирования, следует ввести знак равенства или символьного равенства. В первом случае интегрирование будет проведено численным методом, во втором — в случае успеха, будет найдено точное значение интеграла с помощью символьного процессора Mathcad (листинг 1).
Листинг .1. Численное и символьное вычисление определенного интеграла ПРАКТИЧЕСКАЯ ЧАСТЬ Решение задач на интегрирование функций в среде Mathcad. 1.Вычислить неопределенные интегралы тремя способами: по правилу 3: 1) по правилу 5: 4) по правилу 6 проинтегрируйте функции: 7) 2.По правилу 3 найти значение определенного интеграла 3.Найти интеграл функции а) методами Mathcad; б) методом прямоугольников; в) методом трапеций; г) методом парабол. Указания: - присвоить значения пределам интегрирования и шагу разбиения:
а:=0, b:=1, n:=20, h:= (b - a)/n - - присвоить переменной х следующее изменение значений: х:=a,a+h..b. - вывести на экран значения функции F(x). - ввести формулы прямоугольников: - вычислить значение интеграла по формуле трапеций: - вычислить интеграл по формуле парабол: оценить точность вычислений. Для этого достаточно рассмотреть абсолютную разность между точным значением интеграла (I) и приближенным (I1, I2, I3, I4). 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 (1.1)
(1.1)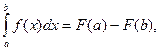 (1.2)
(1.2) на отрезке [a; b], то
на отрезке [a; b], то 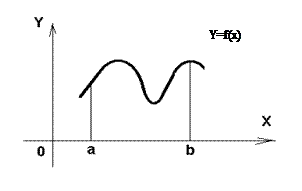
 . Точки деления будут: x0=a; x1=a+h; x2=a+2×h, ... ,
. Точки деления будут: x0=a; x1=a+h; x2=a+2×h, ... , (1.3)
(1.3) (1.4)
(1.4) (1.5)
(1.5)
 (1.6)
(1.6)
 . Обозначим точки разбиения x0=a; x1=x0+h, ... , xi=x0+i×h, ..., x2n=b. Значения функции f в точках xi обозначим yi, т.е. yi=f(xi). Тогда согласно методу Симпсона
. Обозначим точки разбиения x0=a; x1=x0+h, ... , xi=x0+i×h, ..., x2n=b. Значения функции f в точках xi обозначим yi, т.е. yi=f(xi). Тогда согласно методу Симпсона
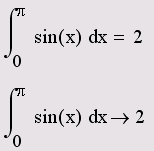
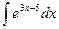 ; 2)
; 2)  ; 3)
; 3)  ;
; ; 5)
; 5)  6)
6)  ;
;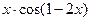 ; 8)
; 8)  .
. .
. , заданной на интервале
, заданной на интервале  различными способами:
различными способами: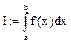 . Далее найти значение I средствами Mathcad.
. Далее найти значение I средствами Mathcad.
 - левая и правая формулы прямоугольников.
- левая и правая формулы прямоугольников. .
.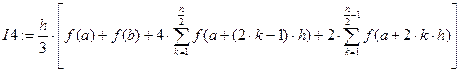 .
.