
|
|
Условия независимости криволинейного интеграла II рода от пути интегрирования
Рассмотрим криволинейный интеграл
Рассмотрим две произвольные кривые MPN и MQN, лежащие в рассматриваемой области D и соединяющие точки М и N. Пусть
т.е.
Тогда на основании свойств 1 и 4 криволинейных интегралов имеем:
т.е. интеграл по замкнутому контуру L
В последней формуле криволинейный интеграл взят по замкнутому контуру L, составленному из кривых MPN и NQM. Этот контур L можно, очевидно, считать произвольным. Таким образом, из условия: что для любых двух точек М и N криволинейный интеграл не зависит от формы соединяющей их кривой, а зависит только от положения этих точек, следует, что криволинейный интеграл по любому замкнутому контуру равен нулю. Справедливо и обратное заключение: если криволинейный интеграл по любому замкнутому контуру равен нулю, то этот криволинейный интеграл не зависит от формы кривой, соединяющей две любые точки, а зависит только от положения этих точек. Действительно, что из равенства (2) следует равенство (1) Теорема Пусть во всех точках некоторой области D функции Р(х, у), Q(x, y) вместе со своими частными производными необходимо и достаточно выполнение равенства во всех точках области D. Доказательство Рассмотрим произвольный замкнутый контур L в области D и для него напишем формулу Грина:
Если выполняется условие (3), то двойной интеграл, стоящий слева, тождественно равен нулю и, следовательно,
Таким образом, достаточность условия (3) доказана. Докажем теперь необходимость этого условия, т.е. докажем, что если равенство (2) выполняется для любой замкнутой кривой L в области D, то в каждой точке этой области выполняется условие (3). Допустим, напротив, что равенство (2) выполняется, т.е.
а условие (3) не выполняется, т.е.
хотя бы в одной точке. Пусть, например, в некоторой точке
Так как в левой части неравенства стоит непрерывная функция, то она будет положительна и больше некоторого числа
Но по формуле Грина левая часть последнего неравенства равна криволинейному интегралу по границе
во всех точках данной области D.
Таким образом, теорема полностью доказана. При изучении дифференциальных уравнений было доказано, что выполнение условия
равносильно тому, что выражение Pdx + Qdy есть полный дифференциал некоторой функции u(x, y), т.е.
причем
Но в этом случае вектор
есть градиент функции u(x, y); Функция u(x, y), градиент которой равен вектору Докажем, что в этом случае криволинейный интеграл
Доказательство Если Рdx + Qdy является полным дифференциалом функции u(x, y), то
Для вычисления этого интеграла напишем параметрические уравнения кривой L, соединяющей точки М и N:
Будем считать, что значению параметра
Выражение, стоящее в скобках, есть функция от t, являющаяся полной производной от функции
Как мы видим, криволинейный интеграл от полного дифференциала не зависит от формы кривой, по которой производится интегрирование. Таким образом: условия независимости криволинейных интегралов II рода от формы пути интегрирования следующие: Если в некоторой области P(x, y) и Q(x, y) непрерывны вместе со своими 1. 2. интеграл вдоль всякой замкнутой кривой L, лежащей в области D равен нулю. 3. существует такая функция u(x, y), для которой выражение Pdx + Qdy есть полный дифференциал, т.е. P(x, y)dx + Q(x, y)dy = du. 4. в данной области выполнялось бы условие
в каждой точке области D. Для вычисления интеграла, не зависящего от контура интегрирования следует выбрать в качестве наивыгоднейшего пути интегрирования ломаную, соединяющую точки Подынтегральное выражение P(x, y)dx + Q(x, y)dy при указанных условиях являются полным дифференциалом некоторой функции u= u(x, y) т.е. du(x, y) = P(x, y)dx + Q(x, y)dy Функцию u(x, y) (первообразную) можно найти, если вычислить соответствующий криволинейный интеграл по ломаной Получаем следующую формулу:
Аналогично, интегрируя по ломаной
Примеры 1. Вычислить Данный интеграл не зависит от контура интегрирования, т.к.
т.е. Выберем в качестве пути интегрирования ломаную, звенья которой параллельны осям координат. На первом участке:
На втором участке:
Следовательно,
2. Найти первообразную u, если
Пусть
3. Найти
Здесь начальную точку в начале координат взять нельзя, т.к. в этой точке функции Р(х, у) и Q(x, y) не определены, а потому за начальную точку возьмем, например,
4. Найти площадь, ограниченную эллипсом Площадь фигуры, расположенной в плоскости ХОУ и ограничена замкнутой линией С, вычисляется по формуле
где контур С обходим в положительном направлении. Преобразуем криволинейный интаграл в определенный, произведя замену
Параметр t пробегает значения от 0 до 2π. Таким образом
3.Высичлить криволинейный интеграл по длине дуги L, если L – это арка циклоиды
ЗАДАНИЕ ПО ТЕМЕ “КРИВОЛИНЕЙНЫЙ ИНТЕГРАЛ”
Вариант 1 1. Вычислить криволинейный интеграл по длине дуги (декартовые координаты).
2. Вычислить криволинейный интеграл 3. Вычислить криволинейный интеграл 4. Применяя формулу Грина, вычислить интеграл 5. Установить, выполняется ли условие независимости интеграла от пути интегрирования для интеграла 6. Проверить, является ли заданное выражение полным дифференциалом функции U(x,y), и найти ее.
7. Силовое поле образовано силой F(x,y), равной расстоянию точки ее приложения от начала координат и направленной в начало координат. Найти работу силы поля, затраченную на перемещение материальной точки единичной массы по дуге параболы y2=8x от точки (2;4) до точки (4;4
Вариант 2
1. Вычислить криволинейный интеграл по длине дуги (декартовые координаты).
2. Вычислить криволинейный интеграл 3. Вычислить криволинейный интеграл 4. Применяя формулу Грина, вычислить интеграл 5. Установить, выполняется ли условие независимости интеграла от пути интегрирования для интеграла 6. Проверить, является ли заданное выражение полным дифференциалом функции U(x,y), и найти ее.
7. В каждой точке силового поля сила имеет направление отрицательной полуоси ординат и равна квадрату абсциссы точки приложения. Найти работу поля при перемещении единичной массы по параболе
Вариант 3 1. Вычислить криволинейный интеграл по длине дуги (декартовые координаты). 1. 2. Вычислить криволинейный интеграл 3. Вычислить криволинейный интеграл 4. Применяя формулу Грина, вычислить интеграл 5. Установить, выполняется ли условие независимости интеграла от пути интегрирования для интеграла 6. Проверить, является ли заданное выражение полным дифференциалом функции U(x,y), и найти ее.
7. Вычислить работу силы
Вариант 4. 1. Вычислить криволинейный интеграл по длине дуги (декартовые координаты). 1. 2. Вычислить криволинейный интеграл 3. Вычислить криволинейный интеграл 4. Применяя формулу Грина, вычислить интеграл 5. Установить, выполняется ли условие независимости интеграла от пути интегрирования для интеграла 6. Проверить, является ли заданное выражение полным дифференциалом функции U(x,y), и найти ее.
7. В каждой точке окружности
Варивнт 5. 1. Вычислить криволинейный интеграл по длине дуги (декартовые координаты).
2. Вычислить криволинейный интеграл 3. Вычислить криволинейный интеграл 4. Применяя формулу Грина, вычислить интеграл 5. Установить, выполняется ли условие независимости интеграла от пути интегрирования для интеграла 6. Проверить, является ли заданное выражение полным дифференциалом функции U(x,y), и найти ее.
7. Поле образованно силой /
Вариант 6. 1. Вычислить криволинейный интеграл по длине дуги (декартовые координаты).
2. Вычислить криволинейный интеграл 3. Вычислить криволинейный интеграл 4. Применяя формулу Грина, вычислить интеграл 5. Установить, выполняется ли условие независимости интеграла от пути интегрирования для интеграла 6. Проверить, является ли заданное выражение полным дифференциалом функции U(x,y), и найти ее.
7. Найти работу упругой силы
Вариант 7. 1. Вычислить криволинейный интеграл по длине дуги (декартовые координаты).
2. Вычислить криволинейный интеграл 3. Вычислить криволинейный интеграл 4. Применяя формулу Грина, вычислить интеграл 5. Установить, выполняется ли условие независимости интеграла от пути интегрирования для интеграла 6. Проверить, является ли заданное выражение полным дифференциалом функции U(x,y), и найти ее.
7. Материальная точка единичной массы перемещается по окружности
Вариант 8.
1. Вычислить криволинейный интеграл по длине дуги (декартовые координаты).
2. Вычислить криволинейный интеграл 3. Вычислить криволинейный интеграл 4. Применяя формулу Грина, вычислить интеграл 5. Установить, выполняется ли условие независимости интеграла от пути интегрирования для интеграла 6. Проверить, является ли заданное выражение полным дифференциалом функции U(x,y), и найти ее.
7. Материальная точка перемещается по эллипсу
Вариант 9.
1. Вычислить криволинейный интеграл по длине дуги (декартовые координаты).
А 2. Вычислить криволинейный интеграл 3. Вычислить криволинейный интеграл 4. Применяя формулу Грина, вычислить интеграл 5. Установить, выполняется ли условие независимости интеграла от пути интегрирования для интеграла 6. Проверить, является ли заданное выражение полным дифференциалом функции U(x,y), и найти ее.
7. В каждой точке кривой
Вариант 10.
1. Вычислить криволинейный интеграл по длине дуги (декартовые координаты).
В (1;3). 2. Вычислить криволинейный интеграл 3.Вычислить криволинейный интеграл 4. Применяя формулу Грина, вычислить интеграл 5. Установить, выполняется ли условие независимости интеграла от пути интегрирования для интеграла 6. Проверить, является ли заданное выражение полным дифференциалом функции U(x,y), и найти ее.
7. В каждой точке линии
Вариант 11
1. Вычислить криволинейный интеграл по длине дуги (декартовые координаты).
2. Вычислить криволинейный интеграл 3. Вычислить криволинейный интеграл 4. Применяя формулу Грина, вычислить интеграл 5. Установить, выполняется ли условие независимости интеграла от пути интегрирования для интеграла 6. Проверить, является ли заданное выражение полным дифференциалом функции U(x,y), и найти ее.
7. В каждой точке кривой
Вариант 12 1. Вычислить криволинейный интеграл по длине дуги (декартовые координаты).
2. Вычислить криволинейный интеграл 3. Вычислить криволинейный интеграл 4. Применяя формулу Грина, вычислить интеграл 5. Установить, выполняется ли условие независимости интеграла от пути интегрирования для интеграла 6. Проверить, является ли заданное выражение полным дифференциалом функции U(x,y), и найти ее.
7. В каждой точке ломанной Вариант 13. 1. Вычислить криволинейный интеграл по длине дуги (декартовые координаты).
2. Вычислить криволинейный интеграл 3. Вычислить криволинейный интеграл 4. Применяя формулу Грина, вычислить интеграл 5. Установить, выполняется ли условие независимости интеграла от пути интегрирования для интеграла 6. Проверить, является ли заданное выражение полным дифференциалом функции U(x,y), и найти ее.
7. В каждой точке кривой
Вариант 14. 1. Вычислить криволинейный интеграл по длине дуги (декартовые координаты).
2. Вычислить криволинейный интеграл 3. Вычислить криволинейный интеграл 4. Применяя формулу Грина, вычислить интеграл 5. Установить, выполняется ли условие независимости интеграла от пути интегрирования для интеграла 6. Проверить, является ли заданное выражение полным дифференциалом функции U(x,y), и найти ее.
7. В каждой точке кривой
Вариант 15 1. Вычислить криволинейный интеграл по длине дуги (декартовые координаты).
2. Вычислить криволинейный интеграл 3. Вычислить криволинейный интеграл 4. Применяя формулу Грина, вычислить интеграл 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|

 взятый по некоторой плоской кривой L, соединяющей точки М и N. Будем предполагать, что функции Р(х, у) и Q(x, y) имеют непрерывные частные производные в рассматриваемой области D. Выясним, при каких условиях написанный криволинейный интеграл не зависит от формы кривой L, а зависит только от положения начальной и конечной точек М и N.
взятый по некоторой плоской кривой L, соединяющей точки М и N. Будем предполагать, что функции Р(х, у) и Q(x, y) имеют непрерывные частные производные в рассматриваемой области D. Выясним, при каких условиях написанный криволинейный интеграл не зависит от формы кривой L, а зависит только от положения начальной и конечной точек М и N. (1)
(1)

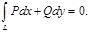 (2)
(2) и
и  непрерывны. Тогда, для того, чтобы криволинейный интеграл по любому замкнутому контуру L, лежащему в этой области, был равен нулю, т.е. чтобы
непрерывны. Тогда, для того, чтобы криволинейный интеграл по любому замкнутому контуру L, лежащему в этой области, был равен нулю, т.е. чтобы (2΄)
(2΄) (3)
(3)



 имеем неравенство
имеем неравенство .
. во всех точках некоторой достаточно малой области
во всех точках некоторой достаточно малой области  , содержащей точку
, содержащей точку  . Возьмем двойной интеграл в этой области от разности
. Возьмем двойной интеграл в этой области от разности  . Он будет иметь положительное значение. Действительно,
. Он будет иметь положительное значение. Действительно,
 области
области 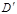 , который, по предположению равен нулю. Следовательно, последнее неравенство противоречит условию (2), и значит, предположение, что
, который, по предположению равен нулю. Следовательно, последнее неравенство противоречит условию (2), и значит, предположение, что  отлично от нуля хотя бы в одной точке, не верно. Отсюда вытекает, что
отлично от нуля хотя бы в одной точке, не верно. Отсюда вытекает, что


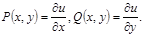

 , называется потенциалом этого вектора.
, называется потенциалом этого вектора. по любой кривой L, соединяющей точки М и N, равняется разности значений функции и в этих точках:
по любой кривой L, соединяющей точки М и N, равняется разности значений функции и в этих точках:
 и криволинейный интеграл примет вид
и криволинейный интеграл примет вид

 соответствует точка М, а значению t = T – точка N. Тогда криволинейный интеграл сведется к следующему определенному интегралу:
соответствует точка М, а значению t = T – точка N. Тогда криволинейный интеграл сведется к следующему определенному интегралу:
 по t. Поэтому
по t. Поэтому
 и
и  , то:
, то: в области D не зависит от формы пути интегрирования, если его значения по всевозможно кусочно-гладким кривым, лежащим в данной области и, имеющим общее начало и общий конец одинаковы.
в области D не зависит от формы пути интегрирования, если его значения по всевозможно кусочно-гладким кривым, лежащим в данной области и, имеющим общее начало и общий конец одинаковы.

 и
и 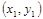 , звенья которой параллельны осям Ох и Оу.
, звенья которой параллельны осям Ох и Оу. где
где 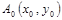 - любая фиксированная точка, В(х, у) – переменная точка, а точка
- любая фиксированная точка, В(х, у) – переменная точка, а точка  - имеет координаты х и
- имеет координаты х и 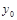 . Тогда вдоль
. Тогда вдоль  имеем
имеем 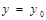 и dy = 0, а вдоль
и dy = 0, а вдоль  имеем x = const и dx = 0.
имеем x = const и dx = 0.
 где
где  получим
получим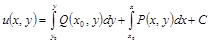




 .
.




 и контуром К является ломаная OMN. Тогда
и контуром К является ломаная OMN. Тогда
 , если
, если

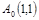 . Тогда
. Тогда
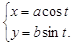
 ,
,


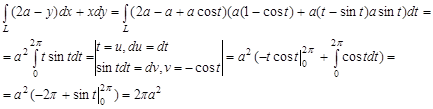
 где L – отрезок прямой
где L – отрезок прямой  точки A (0;-2) и B (4;0) принадлежащие плоскости XOY.
точки A (0;-2) и B (4;0) принадлежащие плоскости XOY. вдоль ломаной L:OAB, где O(0,0), A(2,0), B(4,5). Обход контура против часовой стрелки.
вдоль ломаной L:OAB, где O(0,0), A(2,0), B(4,5). Обход контура против часовой стрелки. по координатам, если L – дуга эллипса
по координатам, если L – дуга эллипса  лежащая в I-й четверти.Обход контура по часовой стрелке.
лежащая в I-й четверти.Обход контура по часовой стрелке. где L – контур треугольника с вершинами A(1,1), B(2,2), C(1,3). Обход контура против часовой стрелки.
где L – контур треугольника с вершинами A(1,1), B(2,2), C(1,3). Обход контура против часовой стрелки. , и найти его.
, и найти его.
 ).
). где L – отрезок прямой соединяющей точки О (0;0) и А (1;2).
где L – отрезок прямой соединяющей точки О (0;0) и А (1;2). , если L – дуга параболы
, если L – дуга параболы  от точки A(-1;1) до точки B(1,1). Обход контура против часовой стрелки.
от точки A(-1;1) до точки B(1,1). Обход контура против часовой стрелки. если L – дуга окружности
если L – дуга окружности 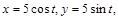 лежащая в 1 и 2 квадратах. Обход контура по часовой стрелке.
лежащая в 1 и 2 квадратах. Обход контура по часовой стрелке.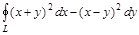 , где L – контур, образованный линией
, где L – контур, образованный линией  и отрезком оси OX при
и отрезком оси OX при  Обход контура против часовой стрелки.
Обход контура против часовой стрелки. , и найти его.
, и найти его.
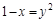 от точки (1,0) до точки (0,1).
от точки (1,0) до точки (0,1). где L – дуга параболы
где L – дуга параболы 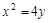 отсеченная параболой
отсеченная параболой  .
.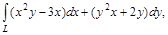 если L- отрезок прямой, соединение точки А(0,1), В(2,3). Обход контура против часовой стрелки.
если L- отрезок прямой, соединение точки А(0,1), В(2,3). Обход контура против часовой стрелки. если L – дуга первой арки циклоиды
если L – дуга первой арки циклоиды  .Обход контура по часовой стрелке.
.Обход контура по часовой стрелке. где L – эллипс
где L – эллипс  Обход контура против часовой стрелки.
Обход контура против часовой стрелки. , и найти его.
, и найти его.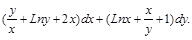
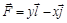 при перемещении материальной точки вдоль верхней половины эллипса
при перемещении материальной точки вдоль верхней половины эллипса  из точки А (а,0), в точку В (-а, 0).
из точки А (а,0), в точку В (-а, 0). где L – контур квадрата
где L – контур квадрата 
 если L – дуга параболы
если L – дуга параболы  точки А(0,0), до точки В (1,1). Обход контура против часовой стрелки.
точки А(0,0), до точки В (1,1). Обход контура против часовой стрелки. Обход контура по часовой стрелке.
Обход контура по часовой стрелке. где L – контур треугольника с вершинами А (1;0), В (1;1), С (0,1). Обход контура против часовой стрелки.
где L – контур треугольника с вершинами А (1;0), В (1;1), С (0,1). Обход контура против часовой стрелки. , и найти его.
, и найти его.
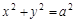 приложена сила
приложена сила  , прекциями которой на оси координат являются
, прекциями которой на оси координат являются  Определить работу силы
Определить работу силы  где L – отрезок прямой, соединяющий точки 0 (0,0), и А (4;2)
где L – отрезок прямой, соединяющий точки 0 (0,0), и А (4;2) 

 если L – дуга кривой
если L – дуга кривой  соединяющей точки А(0,1), до точки В (-1,е). Обход контура против часовой стрелки.
соединяющей точки А(0,1), до точки В (-1,е). Обход контура против часовой стрелки. если L – 1-я четверть окружности
если L – 1-я четверть окружности 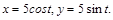 Обход контура по часовой стрелке.
Обход контура по часовой стрелке. где L – контур, ограниченный
где L – контур, ограниченный  и
и  Обход контура против часовой стрелки.
Обход контура против часовой стрелки. , и найти его.
, и найти его.
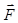 / =
/ =  направление которое составляет угол
направление которое составляет угол  с направлением радиус – вектора
с направлением радиус – вектора 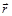 точки ее приложения. Найти работу поля при перемещении материальной точки массы m по дуге окружности
точки ее приложения. Найти работу поля при перемещении материальной точки массы m по дуге окружности  лежащая в I квадранте.
лежащая в I квадранте.  если L – ломанная АВС, А(1;2), В (1;5), C(3;5). Обход контура против часовой стрелки.
если L – ломанная АВС, А(1;2), В (1;5), C(3;5). Обход контура против часовой стрелки. если L – верхняя половина окружности
если L – верхняя половина окружности  Обход контура по часовой стрелке.
Обход контура по часовой стрелке. где L – контур, ограниченный
где L – контур, ограниченный  ,
,  Обход контура против часовой стрелки.
Обход контура против часовой стрелки.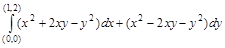 , и найти его.
, и найти его.
 лежащую в Iквадранте. Величина этой силы пропорциональна удалению точки от начала координат.
лежащую в Iквадранте. Величина этой силы пропорциональна удалению точки от начала координат. где L –часть параболы
где L –часть параболы 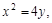 от точки (1, 1/4) до точки (2;1).
от точки (1, 1/4) до точки (2;1). 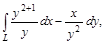 где L – отрезок прямой, соединяющей точки В(1;2) и В (2;4). Обход контура против часовой стрелки.
где L – отрезок прямой, соединяющей точки В(1;2) и В (2;4). Обход контура против часовой стрелки.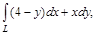 если L – первая арка циклоиды
если L – первая арка циклоиды  Обход контура по часовой стрелке.
Обход контура по часовой стрелке.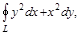 где L – окружность
где L – окружность  Обход контура против часовой стрелки.
Обход контура против часовой стрелки. , и найти его.
, и найти его.
 под действием силы
под действием силы  . Построить силу в начале каждой окружности. Найти работу по контуру.
. Построить силу в начале каждой окружности. Найти работу по контуру. где L – контур прямоугольника с вершинами в точках 0 0(0;0), А (4;0), В (4;2), С (0;2).
где L – контур прямоугольника с вершинами в точках 0 0(0;0), А (4;0), В (4;2), С (0;2).  если L – дуга параболы
если L – дуга параболы  если L – часть окружности
если L – часть окружности  лежащая в квадрате 1. Обход контура по часовой стрелке.
лежащая в квадрате 1. Обход контура по часовой стрелке. где L – контур треугольника с вершинами А (0;0), В (1;0), С (0;1).Обход контура против часовой стрелки.
где L – контур треугольника с вершинами А (0;0), В (1;0), С (0;1).Обход контура против часовой стрелки. , и найти его.
, и найти его.
 под действием силы
под действием силы  где L – дуга параболы
где L – дуга параболы  лежащая между точками
лежащая между точками , В (2;2).
, В (2;2).  если L – отрезок прямой, соединяющей точки А(5;0) и В(0,5). Обход контура против часовой стрелки.
если L – отрезок прямой, соединяющей точки А(5;0) и В(0,5). Обход контура против часовой стрелки. если L – дуга эллипса
если L – дуга эллипса 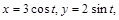 между точками, соответствующими
между точками, соответствующими  Обход контура по часовой стрелке.
Обход контура по часовой стрелке.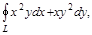 где L – окружность
где L – окружность  Обход контура против часовой стрелки.
Обход контура против часовой стрелки. , и найти его.
, и найти его.
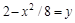 приложена сила
приложена сила  Определить работу силы
Определить работу силы  где L –отрезок прямой, соединяющей точки А
где L –отрезок прямой, соединяющей точки А 
 если L – дуга кривой
если L – дуга кривой  от точки А(1;0) до В(е,5). Обход контура против часовой стрелки.
от точки А(1;0) до В(е,5). Обход контура против часовой стрелки. если L – дуга окружности
если L – дуга окружности  где L – контур треугольника с вершинами А (1;0), В (2;0), С (1;2). Обход контура против часовой стрелки.
где L – контур треугольника с вершинами А (1;0), В (2;0), С (1;2). Обход контура против часовой стрелки. , и найти его.
, и найти его.
 приложена сила
приложена сила  Вычислите работу, совершенную силой
Вычислите работу, совершенную силой  где L – дуга параболы
где L – дуга параболы  от точки (0;0) до точки (1;
от точки (0;0) до точки (1;  если L – ломаная ОАВ: О(0;0), А(1;0), В(0;1). Обход контура против часовой стрелки.
если L – ломаная ОАВ: О(0;0), А(1;0), В(0;1). Обход контура против часовой стрелки. если L –дуга эллипсса
если L –дуга эллипсса  , между точками А(0;1) и В(
, между точками А(0;1) и В(  ).Обход контура по часовой стрелке.
).Обход контура по часовой стрелке. где L –контур, ограниченный линиями
где L –контур, ограниченный линиями  Обход контура против часовой стрелки.
Обход контура против часовой стрелки.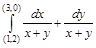 , и найти его.
, и найти его. .
. Найти работу, совершенную силой
Найти работу, совершенную силой  где L – отрезок прямой
где L – отрезок прямой  , соединяющий точки (0;-2) и (4;0).
, соединяющий точки (0;-2) и (4;0). если L–дуга параболы:
если L–дуга параболы:  если L – первая арка циклоиды
если L – первая арка циклоиды  . Обход контура по часовой стрелке.
. Обход контура по часовой стрелке. где L –контур, ограниченный линиями
где L –контур, ограниченный линиями  Обход контура против часовой стрелки.
Обход контура против часовой стрелки. , и найти его.
, и найти его. .
. приложена сила
приложена сила  где L – отрезок прямой
где L – отрезок прямой  если L–дуга синусоиды:
если L–дуга синусоиды:  , от х=0 до х=
, от х=0 до х= 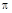 . Обход контура против часовой стрелки.
. Обход контура против часовой стрелки. если L – часть окружности
если L – часть окружности  лежащая в верхней полуплоскости. Обход контура по часовой стрелке.
лежащая в верхней полуплоскости. Обход контура по часовой стрелке. где L –контур, ограниченный хордой АВ, где А (1;0), В(2;3), и параболой, проходящей через эти точки, и осью симметрии ОУ. Обход контура против часовой стрелки.
где L –контур, ограниченный хордой АВ, где А (1;0), В(2;3), и параболой, проходящей через эти точки, и осью симметрии ОУ. Обход контура против часовой стрелки. , и найти его.
, и найти его. .
. приложена сила
приложена сила  . Величина этой силы равна квадрату абсциссы точки кривой. Найти работу, совершенную силой
. Величина этой силы равна квадрату абсциссы точки кривой. Найти работу, совершенную силой  где L – часть окружности
где L – часть окружности 
 если L–дуга полукубической параболы
если L–дуга полукубической параболы  соединящие точки А(1;1) и В(8;4).Обход контура против часовой стрелки.
соединящие точки А(1;1) и В(8;4).Обход контура против часовой стрелки. если L – дуга окружности
если L – дуга окружности  лежащая в I квадранте. Обход контура по часовой стрелке.
лежащая в I квадранте. Обход контура по часовой стрелке. где L –окружность
где L –окружность 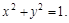 Обход контура против часовой стрелки.
Обход контура против часовой стрелки. , и найти его.
, и найти его. .
. Найти работу, совершенную силой
Найти работу, совершенную силой  где L – дуга кубической параболы
где L – дуга кубической параболы  ,если L – отрезок прямой, соединяющий точки A(0,0) и B(3,6). Обход контура против часовой стрелки.
,если L – отрезок прямой, соединяющий точки A(0,0) и B(3,6). Обход контура против часовой стрелки. если L – часть окружности
если L – часть окружности  , лежащая в IV квадранте. Обход контура по часовой стрелке.
, лежащая в IV квадранте. Обход контура по часовой стрелке. где L – окружность
где L – окружность  Обход контура против часовой стрелки.
Обход контура против часовой стрелки.