
|
|
Момент инерции площади плоской фигурыМоментом инерции I материальной точки М с массой m, относительно некоторой точки 0 называется произведение массы m на квадрат ее расстояния r от точки 0:
Найдем момент инерции материальной плоской фигуры s. Пусть область s расположена в плоскости OXY и поверхностная плотность всюду равна единице . Разобъем область s на элементарные площадки Элементарным моментом инерции т.е.
Составим сумму таких моментов: Пусть диаметр каждой элементарной площадки Dsi ®0, тогда предел этой интегральной суммы будет двойной интеграл
Следовательно, момент инерции области s относительно начала координат равен
где s - область, совпадающая с данной плоской фигурой. Интегралы
называются соответственно моментами инерции области s относительно осей OX и OY. Замечание Если поверхностная плотность не равна единице, а есть функция от x и y, т.е. m=m(x,y), то момент инерции плоской фигуры относительно начала координат Координаты центра тяжести плоской фигуры Координаты центра тяжести системы материальных точек
Найдем координаты центра тяжести плоской фигуры s. Разобьем фигуру s на n частей Ds1, Ds2¼Dsn . Пусть поверхностная плотность mº1, тогда масса Dsi будет равна ее площади. Считаем, что масса элементарной площадки Dsi сосредоточена в точке
Пусть Dsi ®0, тогда предел этих интегральных сумм будет равен двойному интегралу, т.е.
Примечание Если фигура имеет любую переменную во всех точках поверхностную плотность: m=m(x,y), то
Выражения
называются статическими моментами плоской фигуры s относительно осей OY и OX. Интеграл
Примеры
1. Вычислить объем тела ограниченного поверхностями :
2.Найти массу кругового кольца, если в каждой его точке поверхностная плотность обратно пропорциональна квадрату расстояния от центра (радиусы r1 и r2) (r2 >r1)
Если δ(М) - поверхностная плотность в точке М(х, у) плоской фигуры (или материальной пластинки) которая занимает обдасть D, то ее масса вычисляется по формуле
В данном случае δ(М) = к/ρ , где к – коэффициент пропорциональности, ρ – расстояние точки М(х, у) от начала координат. Обозначим радиусы окружностей, ограничивающих кольцо через r1 и r2 (r2 >r1). Разместим полюс полярной системы кординат в центре кольца, и запишем уравнения окружностей ρ = r1 , ρ = r2 Массу всего кольца найдем по приведенной формуле, преобразовав ее к полярной системе координат
3. Найти координаты центра тяжести плоской фигуры, ограниченной кардио идой
ЗАДАНИЕ ПО ТЕМЕ “ДВОЙНОЙ ИНТЕГРАЛ”
Вариант 1 1. В двойном интеграле 2.
Изменить порядок интегрирования в двойном интеграле.
3. Вычислить 4. Найти двойным интегрированием объем тела, ограниченного поверхностями.
5. Найти площадь фигуры D, изображенной на рисунке в п. 1. 6. Расставить пределы интегрирования, перейдя к полярным координатам в двойном интеграле
7. Вычислить двойной интеграл по области D, перейдя к полярным координатам в двойном интеграле.
8. Найти площадь фигуры, ограниченной линиями (сделать рисунок).
9. Найти объем тела, ограниченного поверхностями.
10. Найти массу плоской фигуры, ограниченной линей 11. Найти центр тяжести однородной фигуры D: 12. Найти центр тяжести фигуры 13. Вычислить момент инерции круга радиусом R относительно касательной. 14. Вычислить момент инерции площади фигуры
Вариант 2 1. В двойном интеграле
2. Изменить порядок интегрирования в двойном интеграле.
3. Вычислить 4. Найти двойным интегрированием объем тела, ограниченного поверхностями.
5. Найти S области D, фигуры изображенной на рисунке в п. 1. 6. Расставить пределы интегрирования, перейдя к полярным координатам в двойном интеграле
7. Вычислить двойной интеграл по области D, перейдя к полярным координатам в двойном интеграле.
8. Найти площадь фигуры, ограниченной линиями (сделать рисунок).
9. Найти объем тела, ограниченного поверхностями.
10. Найти массу кругового кольца ( 11. Вычислить координаты центра тяжести фигуры D, ограниченной кардиоидой 12. Найти координаты центра тяжести фигуры
13. Вычислить момент площади эллипса 14. Вычислить момент площади прямоугольника, ограниченного прямыми
Вариант 3
1. В двойном интеграле 2.
Изменить порядок интегрирования в двойном интеграле.
3. Вычислить 4. Найти двойным интегрированием объем тела, ограниченного поверхностями.
5. Найти площадь фигуры D, изображенной на рисунке в п. 1. 6. Расставить пределы интегрирования, перейдя к полярным координатам в двойном интеграле
7. Вычислить двойной интеграл по области D, перейдя к полярным координатам в двойном интеграле.
8. Найти площадь фигуры, ограниченной линиями (сделать рисунок).
9. Найти объем тела, ограниченного поверхностями.
10. Наитй массу пластинки, ограничекнной линией 11. Найти координаты центра тяжести фигуры, ограниченной кривой 12. Найти центр тяжести круговой пластинки 13. Найти момент инерции однородного треугольника D: y = 5, y = x+1, y =2x+7 относительно оси OX. 14. Найти момент инерции круга радиусом R относительно точки на окружности (0,0). Вариант 4 1. В двойном интеграле 2.
Изменить порядок интегрирования в двойном интеграле.
3. Вычислить
4. Найти двойным интегрированием объем тела, ограниченного поверхностями.
5. Найти площадь фигуры D, изображенной на рисунке в п. 1. 6. Расставить пределы интегрирования, перейдя к полярным координатам в двойном интеграле
7. Вычислить двойной интеграл по области D, перейдя к полярным координатам в двойном интеграле. 7. 8. Найти площадь фигуры, ограниченной линиями (сделать рисунок).
9. Найти объем тела, ограниченного поверхностями.
10. Наитй массу пластинки, имеющей форму прямоугольного треугольника с катетами OB = a; OA = b, если 11. Найти центр тяжести однородного кругового сектора с центральным углом 2a, радиусом R. 12. Найти центр тяжести фигуры D: 13. Вычислить момент инерции треугольника D: 14. Вычислить момент инерции эллипса
Вариант 5
1. В двойном интеграле
2. Изменить порядок интегрирования в двойном интеграле.
3. Вычислить 4. Найти двойным интегрированием объем тела, ограниченного поверхностями.
5. Найти площадь фигуры D, изображенной на рисунке в п. 1. 6. Расставить пределы интегрирования, перейдя к полярным координатам в двойном интеграле D: 7.
8. Найти площадь фигуры, ограниченной линиями (сделать рисунок).
9. Найти объем тела, ограниченного поверхностями.
10. Найти массу фигуры, ограниченной линией 11. Найти центр тяжести однородной фигуры – кругового сегмента, соответствующего центральному углу a, радиус круга R. 12. Найти центр тяжести фигуры D: 13. Вычислить момент инерции фигуры D: 14. Найти момент инерции фигуры
Вариант 6
1. В двойном интеграле
2.
Изменить порядок интегрирования в двойном интеграле.
3. Вычислить 4. Найти двойным интегрированием объем тела, ограниченного поверхностями.
5. Найти площадь фигуры D, изображенной на рисунке в п. 1. 6. Расставить пределы интегрирования, перейдя к полярным координатам в двойном интеграле
7. Вычислить двойной интеграл по области D, перейдя к полярным координатам в двойном интеграле.
8. Найти площадь фигуры, ограниченной линиями.
9. Найти объем тела, ограниченного поверхностями.
10. Найти массу плоской фигуры, ограниченной линией 11. Найти координаты центра тяжести фигуры, ограниченной параболами 12. Найти координаты центра тяжести фигуры 13. Найти момент инерции фигуры 14. Вычислить момент инерции фигуры
Вариант 7
1. В двойном интеграле
2. Изменить порядок интегрирования в двойном интеграле.
3. Вычислить 4. Найти двойным интегрированием объем тела, ограниченного поверхностями.
5. Найти площадь фигуры D, изображенной на рисунке в п. 1. 6. Расставить пределы интегрирования, перейдя к полярным координатам в двойном интеграле
7. Вычислить двойной интеграл по области D, перейдя к полярным координатам в двойном интеграле
8. Найти площадь фигуры, ограниченной линиями.
9. Найти объем тела, ограниченного поверхностями.
10. Найти массу плоской фигуры, ограниченной линией 11. Определить центр тяжести однородной плоской фигуры, ограниченной кривыми: 12. Найти центр тяжести фигуры 13. Найти момент инерции фигуры 14. Вычислить момент инерции фигуры
Вариант 8
1. В двойном интеграле
2. Изменить порядок интегрирования в двойном интеграле.
3. Вычислить 4. Найти двойным интегрированием объем тела, ограниченного поверхностями.
5. Найти площадь фигуры D, изображенной на рисунке в п. 1. 6. Расставить пределы интегрирования, перейдя к полярным координатам в двойном интеграле
7. Вычислить двойной интеграл по области D, перейдя к полярным координатам в двойном интеграле
8. Найти площадь фигуры, ограниченной линиями.
9. Найти объем тела, ограниченного поверхностями.
10. Найти массу плоской фигуры, ограниченной линией 11. Найти координаты центра тяжести фигуры, ограниченной кривыми 12. Найти координаты центра тяжести фигуры 13. Найти момент инерции равнобедренного треугольника относительно его высоты. Основание треугольника a см, высота h см. 14. Найти момент инерции фигуры, ограниченной линией
Вариант 9
1. В двойном интеграле
2. Изменить порядок интегрирования в двойном интеграле.
3. Вычислить 4. Найти двойным интегрированием объем тела, ограниченного поверхностями.
5. Найти площадь фигуры D, изображенной на рисунке в п. 1. 6. Расставить пределы интегрирования, перейдя к полярным координатам в двойном интеграле
7. Вычислить двойной интеграл по области D, перейдя к полярным координатам в двойном интеграле
8. Найти площадь фигуры, ограниченной линиями.
9. Найти объем тела, ограниченного поверхностями.
10. Найти массу плоской фигуры, ограниченной линией 11. Найти центр тяжести плоской фигуры, ограниченной окружностью 12. Найти центр тяжести фигуры 13. Найти момент инерции фигуры 14. Найти момент инерции фигуры
Вариант 10
1. В двойном интеграле 2.
Изменить порядок интегрирования в двойном интеграле.
3. Вычислить 4. Найти двойным интегрированием объем тела, ограниченного поверхностями.
5. Найти площадь фигуры D, изображенной на рисунке в п. 1. 6. Расставить пределы интегрирования, перейдя к полярным координатам в двойном интеграле
7. Вычислить двойной интеграл по области D, перейдя к полярным координатам в двойном интеграле
8. Найти площадь фигуры, ограниченной линиями.
9. Найти объем тела, ограниченного поверхностями.
10. Найти массу плоской фигуры, ограниченной линией 11. Найти центр тяжести однородной пластины, ограниченной линиями 12. Найти центр тяжести фигуры 13. Найти момент инерции равнобедренной трапеции относительно прямой, соединяющей середины оснований. Размры: большее основание a см, b см, высота h см. 14. Найти момент инерции кругового кольца диаметром d и D относительно его центра.
Вариант 11
1. В двойном интеграле
2. Изменить порядок интегрирования в двойном интеграле.
3. Вычислить 4. Найти двойным интегрированием объем тела, ограниченного поверхностями.
5. Найти площадь фигуры D, изображенной на рисунке в п. 1. 6. Расставить пределы интегрирования, перейдя к полярным координатам в двойном интеграле
7. Вычислить двойной интеграл по области D, перейдя к полярным координатам в двойном интеграле
8. Найти площадь фигуры, ограниченной линиями.
9. Найти объем тела, ограниченного поверхностями.
10. Найти массу плоской фигуры, ограниченной линией 11. Найти центр тяжести однородной плоской фигуры, ограниченной линиями 12. Найти центр тяжести фигуры
13. Найти момент инерции эллиптического кольца, образованного двумя эллипсами, с общим центром и совпадающими осями (концентрические эллипсы). Оси внешнего эллипса a см, b см, а внутреннего a1 см и b1 см. 14. Найти момент инерции однородного круга радиусом R относительно его центра.
Вариант 12
1. В двойном интеграле
2. Изменить порядок интегрирования в двойном интеграле.
3. Вычислить
4. Найти двойным интегрированием объем тела, ограниченного поверхностями.
5. Найти площадь фигуры D, изображенной на рисунке в п. 1. 6. Расставить пределы интегрирования, перейдя к полярным координатам в двойном интеграле
7. Вычислить двойной интеграл по области D, перейдя к полярным координатам в двойном интеграле
8. Найти площадь фигуры, ограниченной линиями.
9. Найти объем тела, ограниченного поверхностями.
10. Найти массу плоской фигуры, ограниченной линией 11. Найти центр тяжести однородной тонкой фигуры, ограниченной линиями 12. Найти центр тяжести фигуры 13. Найти момент инерции однородного сегмента параболы с хордой, перпендикулярной к оси относительно оси OX 14. Вычислить полярный моменте инерции однородной фигуры
Вариант 13 1. В двойном интеграле
2. Изменить порядок интегрирования в двойном интеграле.
3. Вычислить 4. Найти двойным интегрированием объем тела, ограниченного поверхностями.
5. Найти площадь фигуры D, изображенной на рисунке в п. 1. 6. Расставить пределы интегрирования, перейдя к полярным координатам в двойном интеграле
7. Вычислить двойной интеграл по области D, перейдя к полярным координатам в двойном интеграле
8. Найти площадь фигуры, ограниченной линиями. D: 9. Найти объем тела, ограниченного поверхностями.
10. Найти массу плоской фигуры, ограниченной линией 11. Найти центр тяжести фигуры, ограниченной осями координат и линиями 12. Найти центр тяжести фигуры 13. Найти момент инерции фигуры D: 14. Найти момент инерции фигуры
Вариант 14
1. В двойном интеграле
2. Изменить порядок интегрирования в двойном интеграле.
3. Вычислить 4. Найти двойным интегрированием объем тела, ограниченного поверхностями.
5. Найти площадь фигуры D, изображенной на рисунке в п. 1. 6. Расставить пределы интегрирования, перейдя к полярным координатам в двойном интеграле
7. Вычислить двойной интеграл по области D, перейдя к полярным координатам в двойном интеграле
8. Найти площадь фигуры, ограниченной линиями.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|

 Момент инерции системы материальных точек
Момент инерции системы материальных точек 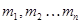 относительно точки 0 есть сумма моментов инерции отдельных точек системы:
относительно точки 0 есть сумма моментов инерции отдельных точек системы:  .
. на каждой площадке возьмем точку
на каждой площадке возьмем точку  с координатами
с координатами  .
.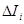 площадки Dsi будет произведение массы площадки Dsi на квадрат расстояния
площадки Dsi будет произведение массы площадки Dsi на квадрат расстояния 

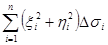 , которая представляет собой интегральную сумму для функции ¦(x,y) = x²+y², по области s.
, которая представляет собой интегральную сумму для функции ¦(x,y) = x²+y², по области s. .
.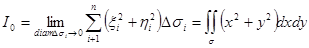




 с массами
с массами  (1)
(1) тогда фигуру s рассмотрим как систему материальных точек. По формулам (1) координаты центра тяжести этой фигуры будут приближенно определяться равенствами:
тогда фигуру s рассмотрим как систему материальных точек. По формулам (1) координаты центра тяжести этой фигуры будут приближенно определяться равенствами:




 выражает величину массы рассматриваемой фигуры.
выражает величину массы рассматриваемой фигуры.






 Разместим полюс в начале координат прямоугольной декартовой системы координат и направим полярную ось вдоль ОХ. Из-за того, что фигура симметрична относительно ОХ, ус = 0. Найдем хс.
Разместим полюс в начале координат прямоугольной декартовой системы координат и направим полярную ось вдоль ОХ. Из-за того, что фигура симметрична относительно ОХ, ус = 0. Найдем хс.
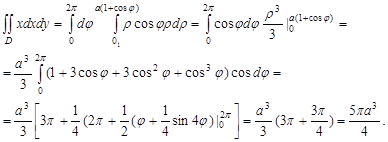


 расставить пределы интегрирования по области D, ограниченной линиями (двумя способами).
расставить пределы интегрирования по области D, ограниченной линиями (двумя способами).

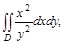 где D:
где D: 

 по области D.
по области D.


 где
где 


 , если поверхностная плоскость в каждой ее точке
, если поверхностная плоскость в каждой ее точке  .
. (полуовал).
(полуовал).
 , если поверхностная плотность в каждой ее точке равна
, если поверхностная плотность в каждой ее точке равна 
 относительно полюса (0,0).
относительно полюса (0,0). расставить пределы интегрирования по области D, ограниченной линиями (двумя способами).
расставить пределы интегрирования по области D, ограниченной линиями (двумя способами).

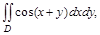 где
где 



 где
где 


 .
. <R),ограниченной указанными линиями, если в каждой ее точке
<R),ограниченной указанными линиями, если в каждой ее точке  обратно пропорциональна квадрату расстояния ее до центра кольца.
обратно пропорциональна квадрату расстояния ее до центра кольца.

 если поверхностная плотность в каждой ее точке равна
если поверхностная плотность в каждой ее точке равна 
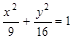 относительно оси OY.
относительно оси OY. относительно начала координат (0,0).
относительно начала координат (0,0).

 где
где 

 по области D.
по области D.

 где
где 



 если плотность в каждой ее точке
если плотность в каждой ее точке  и прямой OA, проходящей через точки (0,0) и
и прямой OA, проходящей через точки (0,0) и 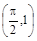 синусоиды.
синусоиды. если поверхностная плотность
если поверхностная плотность 

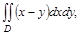 где
где 



 где
где 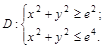



 и
и  если поверхностная плотность
если поверхностная плотность  относительно оси OX.
относительно оси OX. относительно начала координат (0,0).
относительно начала координат (0,0).

 где
где 
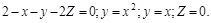

 = 4х; у =х, х = о.
= 4х; у =х, х = о. где
где 



 если поверхностная плоскость в каждой ее точке
если поверхностная плоскость в каждой ее точке 
 если
если  в каждой ее точке равна расстоянию ее до оси OX.
в каждой ее точке равна расстоянию ее до оси OX. относительно оси OX.
относительно оси OX.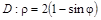 относительно полюса (0,0).
относительно полюса (0,0).
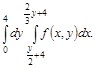
 где
где 



 где
где 
 .
.
 , если поверхностная плоскость в каждой ее точке
, если поверхностная плоскость в каждой ее точке 
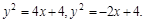
 если поверхностная плоскость
если поверхностная плоскость  относительно оси OY.
относительно оси OY. относительно полюса
относительно полюса  .
.

 где
где 



 где
где 
 .
.
 если поверхностная плоскость в каждой ее точке
если поверхностная плоскость в каждой ее точке 

 если поверхностная плоскость
если поверхностная плоскость 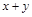 .
. относительно оси OY.
относительно оси OY. относительно полюса (0,0).
относительно полюса (0,0).


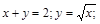

 (меньший из сегментов).
(меньший из сегментов). где
где 
 .
.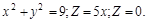
 , если поверхностная плоскость в каждой ее точке
, если поверхностная плоскость в каждой ее точке  и
и  и расположенной в I-й четверти.
и расположенной в I-й четверти.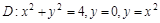 если плотность в каждой ее точке
если плотность в каждой ее точке 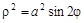 относительно полюса (0,0).
относительно полюса (0,0).

 где
где 


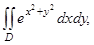 где
где 
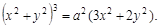

 , если поверхностная плоскость в каждой ее точке
, если поверхностная плоскость в каждой ее точке 
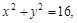 эллипсом
эллипсом  и лежащей в I-й четверти.
и лежащей в I-й четверти.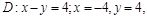 если плотность в каждой ее точке равна
если плотность в каждой ее точке равна 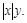
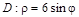 относительно полярной оси.
относительно полярной оси.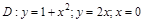 относительно O (0,0).
относительно O (0,0).

 где
где 
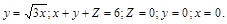

 где
где 


 , если поверхностная плоскость в каждой ее точке
, если поверхностная плоскость в каждой ее точке 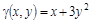 .
.
 , если поверхностная плотность в каждой ее точке равна
, если поверхностная плотность в каждой ее точке равна 



 где
где 


 где
где 
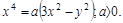
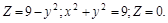
 , если поверхностная плоскость в каждой ее точке
, если поверхностная плоскость в каждой ее точке 

 если
если  в каждой ее точке.
в каждой ее точке.

 где
где 


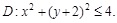


 , если поверхностная плоскость в каждой ее точке
, если поверхностная плоскость в каждой ее точке 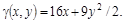

 если поверхностная плотность в каждой ее точке равна
если поверхностная плотность в каждой ее точке равна 
 т.е. относительно начала координат (0,0).
т.е. относительно начала координат (0,0).

 где
где 


 где
где 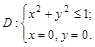 I квадрант
I квадрант

 , если поверхностная плоскость в каждой ее точке
, если поверхностная плоскость в каждой ее точке  .
.
 если поверхностная плотность в каждой ее точке равна
если поверхностная плотность в каждой ее точке равна 
 относительно оси OY.
относительно оси OY. относительно точки O (0,0).
относительно точки O (0,0).

 где
где 


 где
где 
