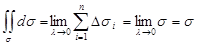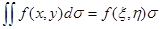|
|
Свойства двойного интегралаЗадача об объеме цилиндрического тела
Рассмотрим в пространстве тело, ограниченное сверху – поверхностью S, заданной уравнением Z=¦(x,y), где ¦(x,y)-непрерывная функция; сбоку – цилиндрической поверхностью с образующими параллельно оси OZ; снизу – областью s (s-проекция поверхности S но XOY)
Найдем объем этого тела. Разобьем область s на п частей: Ds1,Ds2 …Dsп рассмотрим цилиндрические столбики по этим основаниям, ограниченные сверху кусками поверхности S. Объем ΔVi столбика с основанием
где для любой точки Рi (xi,hi) принадлежащей области Dsi строим цилиндр с основанием Dsi и высотой hi=¦(xi,hi). Производя указанные вычисления для каждой области деления и складывая результаты, получим приближенное значение объема тела:
Точное значение объема цилиндрического тела равно пределу, к которому стремится найденное приближенное значение объема при неограниченном измельчении областей деления, т.е. при неограниченном увеличении п (числа областей деления)
Определение двойного интеграла
Пусть в области s плоскости COU задана функция ¦(x,y) Разобьем область s произвольно на п частей: Ds1,Ds2 ,…Dsп так, чтобы Ds1, Ds2 ,…Dsп не имели общих внутренних точек. В каждой Dsi (внутри или на границе) выберем точку Рi (xi ,hi) и умножим значение функции ¦(x,y) в этой точке на площадь Dsi . Сложим все такие произведения, получим
которая называется интегральной суммой для функции ¦(x,y) в области s. Обозначим l - шаг разбиения области s на части Ds1,Ds2 …Dsп. Если при l®0 (при ®0 шага разбиения области s) интегральные суммы (1) имеют конечный предел, то этот предел называется двойным интегралом от функции ¦(x,y) по области s и обозначают
т.е.
где ¦(x,y) – интегральная функция, s - область интегрирования, x,y – переменные интегрирования, ds(dx, dy ) – элемент площади Число I называется пределом интегральных сумм при l®0, если для любого положительного числа e, существует положительное число d, такое, что для всякой интегральной суммы с шагом разбиения d, выполнимо неравенство:
Условия существования двойного интеграла и его свойства Очевидно, функция должна быть ограничена в замкнутой области s, так как в противном случае за счет выбора точки Рi интегральную сумму можно было бы сделать сколько угодно большой по абсолютной величине, а значит не существует конечного предела интегральных сумм при l®0.
Достаточные условия существования двойного интеграла Теорема 1 Если функция ¦(x,y) непрерывна в замкнутой области s, то двойной интеграл этой функции по области s существует. Теорема 2 Если функция ¦(x,y) ограничена в замкнутой области s и непрерывна в ней всюду, кроме конечного числа кусочно-гладких линий, то двойной интеграл по области s существует. Свойства двойного интеграла 1. 2. Постоянный множитель k можно выносить за знак двойного интеграла: или если k – произвольное число , и f(x,y) интегрируема в области s, то kf(x,y) также интегрируема.
3. Двойной интеграл суммы (разности) конечного числа слагаемых равен сумме (разности) двойных интегралов: или если f1(x,y) и f2(x,y) в области s, то их сумма (разность) также интегрируема в области s. Совокупность свойств 2 и 3 называется линейностью интеграла.
4. Если область s разбита на любое число областей Ds1,Ds2 …Dsт, не имеющих общих внутренних точек и в каждой из этих областей функция f(x,y) интегрируема, то
Это свойство называется аддитивностью интеграла 5. Если всюду в области s функция ¦(x,y) положительная, то и двойной интеграл этой функции по области s будет положительным 6. Если всюду в области s функции ¦1 (x,y) и ¦2 (x,y) интегрируемы и ¦1 (x,y)
Это свойство называется монотонностью интеграла. 7. Если ¦ (x,y) интегрируема в областиs, то функция |¦ (x,y)| также интегрируема и
Оценка интеграла по модулю.
8. Если ¦ (x,y)
Доказательство: Так как в данном случае ¦(x,y,z)=1 в области s, то для любого разбиения области s на части Ds1,Ds2 …Dsn получим:
9. Теорема о среднем Если функция непрерывна в замкнутой области s, то в этой области существует точка P(x,h) такая, что
Пусть m – наименьшее значение функции f(x,y) в замкнутой области s; М – наибольшее значение функции f(x,y) в замкнутой области s; тогда для любой точки (x,y) этой области, значения функции удовлетворяют неравенствам: m£¦(x,y)£M Проинтегрируем это неравенство и применим свойства 6, 2, 8:
То есть  или или
Функция ¦(x,y) непрерывна в замкнутой области s, принимает все промежуточные значения между своими наименьшим и наибольшим значениями. Следовательно, существует в области s точка Р(x,h) такая, что
или, что то же

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|

 и высотой hi=¦(xi,hi)Dsi будет равен
и высотой hi=¦(xi,hi)Dsi будет равен ,
,
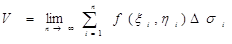

 (1)
(1)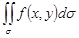 или
или  ,
,


 не зависит от обозначения переменных интегрирования
не зависит от обозначения переменных интегрирования

 ¦2 (x,y), то:
¦2 (x,y), то:

 1, то
1, то