
|
|
Первообразная. Неопределенный интеграл и его свойстваВведение В основу курса положены лекции и практические занятия, на протяжении многих лет реализованные в учебном процессе для специальности “Электропривод и автоматизация промышленных предприятий”. Расположение материала обусловлено не требованиями математической строгости изложения, но чисто утилитарно, с таким расчетом, чтобы аппарат предыдущих разделов мог служить инструментом для изучения последующих. Именно на таком принципе даны многие формулировки основных понятий и развития приложений, основанных на этих понятиях. Для начинающего напомним, что термин “определение” подразумевает “договор” между читателем и остальными пользователями математики по некоторому вопросу для исключения возможных неверных толкований. Это значит, что для понимания вопросов, следующих за определением, определение должно быть “вызубрено”, но не вспоминаться с напряжением. `Текст курса написан не языком “чистого математика” (т.е. определение --> теорема и ее доказательство --> следствия --> обобщение --> новое определение и начинаем сначала ...), а языком для математика-прикладника (определения --> вытекающие из него естественным путем выводы (иногда теоремы с доказательствами) --> отработка навыков использования новых понятий и возможностей --> возможные приложения новых сведений --> переход на введение новых понятий). В текстах сравнительно мало примеров, т.к. это – фактический конспект лекций. Для более полного понимания изучаемого материала предполагается, что читатель будет иметь удовольствие полистать литературу по изучаемому вопросу. Список учебной литературы не приводится из-за его объемности, а также по той причине, что каждый лектор придерживается своего перечня книг. Все приведенные тексты – компиляция книг разных авторов, разного времени издания и разного назначения. Данный курс построен по принципу “понятно лектору – будет понятно и слушателю” и потому представляет собой лоскутное одеяло из разных разделов математики, изложенных в разном стиле. При этом везде преследовалась цель изложения математических принципов в прикладной направленности. Это обнаруживается в большом числе комментариев к теоремам, доказательствам и следствиям.
Неопределенный интеграл Первообразная. Неопределенный интеграл и его свойства Опред. F(x) называют первообразной f(x) (для f(x)) на [a;b] , если для любого х из этого отрезка F(x) дифференцируема и F’(x)=f(x). (По Садовничеву, Сендову стр 314). Так F(x)=x2 будет первообразной для f(x)=2x для всех действительных чисел. Теорема. Если F1(x) и F2(x) первообразные f(x) на [a;b] , то любого х из этого отрезка имеет место равенство F1(x) - F2(x) =С . Док. Положим Ф(х)= F1(x) - F2(x). Тогда Ф(х) дифференцируема и Ф’(х)=0. Т.е. Ф(х)=С. Откуда и следует вывод. Следствие. Если F(x) одна из первообразных для f(x) то любая Ф(х)=F(x)+C – тоже первообразная. Так Ф(x)=2x +С будет первообразной f(x)=x2 для всех действительных чисел. Опред. Множество первообразных для данной f(x) на [a;b] называют неопределенным интегралом и обозначают Из определения следует справедливость тождества Термины и обозначения: f(x) - подынтегральная функция; f(x)dx – подынтегральное выражение; х ( записанный в символе dx) - аргумент (переменная) интегрирования; Все рассмотренное – процесс, обратный поиску производной. Следствия. 1.Производная от НИ равна подынтегральной функции 2.Дифференциал от НИ равен подынтегральному выражению d 3. Неопределенный интеграл от производной равен подынтегральной функции с точностью до постоянного слагаемого С. 4. Неопределенный интеграл от дифференциала равен выражению под знаком дифференциала точностью до постоянного слагаемого С. Все это разные вариации определения. Свойства. 1.Константу - множитель можно выносить из-под знача НИ. Док. Пусть F(x) – первообразная для f(x). Т.е. F’(x)=f(x). Тогда кF(x) – первообразная для кf(x), т.к. (кF(x))’= кF’(x)= кf(x). Т.е. к 2.НИ от суммы функций равен сумме интегралов от слагаемых. Док. Пусть F(x) и Ф(х) – первообразные, соответственно, для f(x) и ф(х). Тогда F’(x)=f(x) и Ф’(х)=ф(х) и потому F(x) f(x) 3.Независимость от аргумента. Так Таблица основных неопределенных интегралов
Комментарий. В отличие от производных, где каждой ситуации предписано правило ее обработки, при поиске интегралов вся теория заканчивается на этой таблице. Фактически для поиска интеграла остаются только определение и следствия из него, свойства и таблица. А это значит, что все остальное следует преобразовывать эвристическими приемами (или по уже готовым рекомендациям, но не правилам!) к таблице и определению. В качестве контроля ответа может служить только обратный процесс – от результата возьми производную. И, если результат равен подынтегральной функции, то имеется некоторая степень уверенности в правильности выполнения интегрирования.
Методы интегрирования. Пусть х=ф(t) –монотонная и непрерывная на некотором промежутке функция. Если на соответствующем промежутке изменения переменной х функция f(x) интегрируема, то справедливо равенство Записанное равенство называют формулой замены в неопределенном интеграле. Применяют ее тогда, когда правая часть оказывается ближе к табличному интегралу (см. Комментарий выше). Док. В самом деле, т.к. F(x) - первообразная для f(x), то F(ф(t)) – будет первообразной для f(ф(t))ф’(t). И потому F’(ф(t))= F’ф(ф(t))ф’t(t)= f(ф(t))ф’(t). Откуда следует f(ф(t))ф’(t)dt= F(ф(t))+C= F(x)+C= Комментарий. Имеются два подхода использования формулы замены. Один из них изложен выше. В другом (более употребимом) случае заменяют не переменную х на некоторое выражение, а выражение, связывающее х, заменяют одной переменной. А далее – как обычно.
= Иногда замену переменных используют в еще одном виде – подведении под знак дифференциала, используя простое соотношение dx= Пример 7.2. Пусть каждая из u(x) и v(x) дифференцируемы на некотором промежутке и существует первообразная для произведения u’(x)v(x). Тогда на этом промежутке существует первообразная для u(x)v’(x) и справедливо равенство
Док. Имеем равенство (uv)’=u’v+v’u. Проинтегрируем его и получим uv =
Комментарии. 1. Рекомендации по применению этой формулы. Т.к. теорема доказана в общем случае, то применять ее можно всегда. . Однако наибольшего эффекта можно добиться, если применять ее , когда под интегралом записано произведение функций Pn(x)eax ; Pn(x)Sinkx (или другая тригонометрическая функция); eaxCoskx (или другая триг. функция ); Pn(x)lnbx и т.д. 2. Возможно одного шага применения формулы недостаточно. Тогда ее приме- няют кратно. 3. Возможно применение формулы приведет к сохранению подынтегрального выражения. Не следует тревожиться по такому случаю, т.к. это даже хорошо. 4. Выбор частей u и v основан на опыте. Только решение конкретных примеров обеспечит навыком выбора частей. Пример 7.3. Простой интеграл

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 .
. - символ интегрирования.
- символ интегрирования.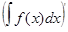 ’=f(x).
’=f(x).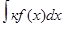 =кF(x)+C.
=кF(x)+C.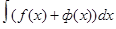 =
= 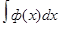 .
. Ф(х) – первообразная для
Ф(х) – первообразная для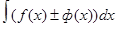 .
.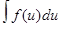 =
= 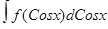 = F(x)= F(u)= F(Cosx) .
= F(x)= F(u)= F(Cosx) .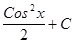 ,
, 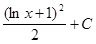 как и для
как и для 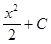 .
. =
= 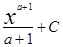 при а
при а  1;
1;  =ех+С;
=ех+С;  =ln
=ln  +C;
+C;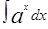 =
=  +С;
+С; 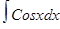 =Sinx+C;
=Sinx+C; 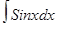 =-Cosx+C;
=-Cosx+C; =tgx+C;
=tgx+C; 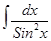 =-ctgx+C;
=-ctgx+C; 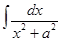 =
=  arctg
arctg 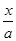 +C;
+C; 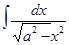 =arcSin
=arcSin  .
. Пример 7.1. Найти
Пример 7.1. Найти  = делаем замену lnx=t,
= делаем замену lnx=t, 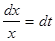 =
=