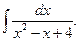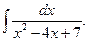Несобственные интегралы I рода
Если положить промежуток интегрирования бесконечным, то приведенное выше определение определенного интеграла теряет смысл, например, потому что невозможно осуществить условия n®¥; l®0 для бесконечного промежутка. Для такого интеграла требуется специальное определение.
Пусть функция y = f(x) определена и непрерывна на полубесконечном промежутке [a;¥), тогда несобственным интегралом с бесконечным пределом  называется предел называется предел  если предел существует. Если этот предел не существует, то не существует и несобственный интеграл. В этом случае принято говорить, что несобственный интеграл расходится. При существовании предела говорят, что несобственный интеграл сходится. если предел существует. Если этот предел не существует, то не существует и несобственный интеграл. В этом случае принято говорить, что несобственный интеграл расходится. При существовании предела говорят, что несобственный интеграл сходится.
Аналогично
 , ,
 . .
Интегралы  , ,  и и  относятся к несобственным интегралам I рода, т. к. для них не выполнено первое условие теоремы Ньютона-Лейбница, а именно один из пределов интегрирования или оба не являются конечными, а второе условие выполнено. Вычисление таких интегралов можно проводить по формуле (22), при этом относятся к несобственным интегралам I рода, т. к. для них не выполнено первое условие теоремы Ньютона-Лейбница, а именно один из пределов интегрирования или оба не являются конечными, а второе условие выполнено. Вычисление таких интегралов можно проводить по формуле (22), при этом  считается как предельное значение, которое может быть конечным, бесконечным или не иметь смысла. То есть: считается как предельное значение, которое может быть конечным, бесконечным или не иметь смысла. То есть:
 , (34) , (34)
 , (35) , (35)
 . (36) . (36)
Пример 34. Вычислить несобственный интеграл или доказать его расходимость:  . .
Данный интеграл является несобственным интегралом I рода, поскольку его верхний предел бесконечен. Воспользовавшись формулой (ююю), получим:

Итак, данный интеграл имеет конечное значение, а следовательно сходится.
Несобственные интегралы II рода
Если в точке 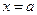 или в точке или в точке 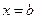 функция функция 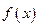 имеет бесконечный разрыв, то есть нарушается второе условие теоремы Ньютона-Лейбница, то интеграл имеет бесконечный разрыв, то есть нарушается второе условие теоремы Ньютона-Лейбница, то интеграл  называется несобственным интегралом II рода. называется несобственным интегралом II рода.
Для вычисления несобственных интегралов II рода пользуются формулой Ньютона-Лейбница, полагая при этом, что значение первообразной  в точке разрыва в точке разрыва 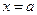  равно предельному значению равно предельному значению   . .
Таким образом формулы для вычисления несобственных интегралов II рода имеют вид:
 , ,
если функция 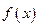 имеет разрыв в точке имеет разрыв в точке 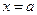 ; ;
 , ,
если функция 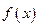 имеет разрыв в точке имеет разрыв в точке 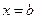 . .
Если предел в правой части равенств существует и конечен, то интеграл называется сходящимся, в противном случае – расходящимся.
Пример 35.
а)Вычислить несобственный инетграл или доказать его расходимость: 
Подынтегральная функция  имеет бесконечный разрыв на отрезке имеет бесконечный разрыв на отрезке  в точке в точке  , т. к. , т. к.  . Следовательно, данный интеграл является несобственным инетгралом II рода. Для его вычисления воспользуемся формулой (///) и получим: . Следовательно, данный интеграл является несобственным инетгралом II рода. Для его вычисления воспользуемся формулой (///) и получим:
 , ,
т.е. данный интеграл сходится.
б)Вычислить несобственный инетграл или доказать его расходимость: 
Подынтегральная функция  имеет бесконечный разрыв на имеет бесконечный разрыв на  в точке в точке  т. к. т. к.  . .

интеграл расходится.
ИНДИВИДУАЛЬНЫЕ РАСЧЕТНЫЕ ЗАДАНИЯ
К РАЗДЕЛУ «ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ»
Найти неопределенный интеграл.
1.1.  . .
1.2. 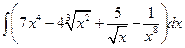 . .
1.3.  . .
1.4.  . .
1.5.  . .
1.6.  . .
1.7.  . .
1.8.  . .
1.9.  . .
1.10.  . .
1.11.  . .
1.12.  . .
1.13.  . .
1.14.  . .
1.15.  . .
1.16.  . .
1.17.  . .
1.18.  . .
1.19.  . .
1.20.  . .
1.21.  . .
1.22.  . .
1.23.  . .
1.24.  . .
1.25. 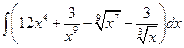 . .
1.26.  . .
1.27.  . .
1.28.  . .
1.29. 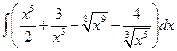 . .
1.30.  . .
Найти неопределенный интеграл.
2.1. 
2.2. 
2.3. 
2.4. 
2.5. 
2.6. 
2.7. 
2.8. 
2.9. 
2.10. 
2.11. 
2.12. 
2.13. 
2.14. 
2.15. 
2.16. 
2.17. 
2.18. 
2.19. 
2.20. 
2.21. 
2.22. 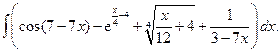
2.23. 
2.24. 
2.25. 
2.26. 
2.27. 
2.28. 
2.29. 
2.30. 
Найти неопределенный интеграл.
3.1. 
| 3.2. 
| 3.3. 
| 3.4. 
| 3.5. 
| 3.6. 
| 3.7. 
| 3.8. 
| 3.9. 
| 3.10. 
| 3.11. 
| 3.12. 
| 3.13. 
| 3.14. 
| 3.15. 
| 3.16. 
| 3.17. 
| 3.18. 
| 3.19. 
| 3.20. 
| 3.21. 
| 3.22. 
| 3.23. 
| 3.24. 
| 3.25. 
| 3.26. 
| 3.27. 
| 3.28. 
| 3.29. 
| 3.30. 
|
Найти неопределенный интеграл.
4.1. 
| 4.2. 
| 4.3. 
| 4.4. 
| 4.5. 
| 4.6. 
| 4.7. 
| 5.8. 
| 4.9. 
| 4.10. 
| 4.11. 
| 4.12. 
| 4.13. 
| 4.14. 
| 4.15. 
| 4.16. 
| 4.17. 
| 4.18. 
| 4.19. 
| 4.20. 
| 4.21. 
| 4.22. 
| 4.23. 
| 4.24. 
| 4.25. 
| 4.26. 
| 4.27. 
| 4.28. 
| 4.29. 
| 4.30. 
|
Найти неопределенный интеграл.
5.1. 
| 5.2. 
| 5.3. 
| 5.4. 
| 5.5. 
| 5.6. 
| 5.7. 
| 5.8. 
| 5.9. 
| 5.10. 
| 5.11. 
| 5.12. 
| 5.13. 
| 5.14. 
| 5.15. 
| 5.16. 
| 5.17. 
| 5.18. 
| 5.19. 
| 5.20. 
| 5.21. 
| 5.22. 
| 5.23. 
| 5.24. 
| 5.25. 
| 5.26. 
| 5.27. 
| 5.28. 
| 5.29. 
| 5.30. 
|
Найти неопределенный интеграл.
6.1. 
| 6.2. 
| 6.3. 
| 6.4. 
| 6.5. 
| 6.6. 
| 6.7. 
| 6.8. 
| 6.9. 
| 6.10. 
| 6.11. 
| 6.12. 
| 6.13. 
| 6.14. 
| 6.15. 
| 6.16. 
| 6.17. 
| 6.18. 
| 6.19. 
| 6.20. 
| 6.21. 
| 6.22. 
| 6.23. 
| 6.24. 
| 6.25. 
| 6.26. 
| 6.27. 
| 6.28. 
| 6.29. 
| 6.30. 
|
Найти неопределенный интеграл.
7.1. 
| 7.2. 
| 7.3. 
| 7.4. 
| 7.5. 
| 7.6. 
| 7.7. 
| 7.8. 
| 7.9. 
| 7.10. 
| 7.11. 
| 7.12. 
| 7.13. 
| 7.14. 
| 7.15. 
| 7.16. 
| 7.17. 
| 7.18. 
| 7.19. 
| 7.20. 
| 7.21. 
| 7.22. 
| 7.23. 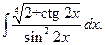
| 7.24. 
| 7.25. 
| 7.26. 
| 7.27. 
| 7.28. 
| 7.29. 
| 7.30. 
|
Найти неопределенный интеграл.
8.1. 
| 8.2. 
| 8.3. 
| 8.4. 
| 8.5.  . .
| 8.6. 
| 8.7. 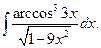
| 8.8. 
| 8.9. 
| 8.10. 
| 8.11. 
| 8.12. 
| 8.13. 
| 8.14. 
| 8.15. 
| 8.16. 
| 8.17. 
| 8.18. 
| 8.19. 
| 8.20. 
| 8.21. 
| 8.22. 
| 8.23. 
| 8.24. 
| 8.25. 
| 8.26. 
| 8.27. 
| 8.28. 
| 8.29. 
| 8.30. 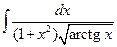
|
Найти неопределенный интеграл.
9.1. 
| 9.2. 
| 9.3. 
| 9.4. 
| 9.5. 
| 9.6. 
| 9.7.  . .
| 9.8. 
| 9.9. 
| 9.10. 
| 9.11. 
| 9.12. 
| 9.13.  . .
| 9.14. 
| 9.15. 
| 9.16. 
| 9.17. 
| 9.18. 
| 9.19. 
| 9.20.  . .
| 9.21. 
| 9.22. 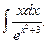
| 9.23. 
| 9.24. 
| 9.25. 
| 9.26. 
| 9.27. 
| 9.28. 
| 9.29. 
| 9.30.  . .
|
Найти неопределенный интеграл.
10.1. 
| 10.2. 
| 10.3. 
| 10.4. 
| 10.5. 
| 10.6. 
| 10.7. 
| 10.8. 
| 10.9. 
| 10.10. 
| 10.11. 
| 10.12. 
| 10.13. 
| 10.14. 
| 10.15. 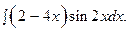
| 10.16. 
| 10.17. 
| 10.18. 
| 10.19. 
| 10.20. 
| 10.21. 
| 10.22. 
| 10.23. 
| 10.24. 
| 10.25. 
| 10.26. 
| 10.27. 
| 10.28. 
| 10.29. 
| 10.30. 
|
Найти неопределенный интеграл.
11.1. 
| 11.2. 
| 11.3. 
| 11.4. 
| 11.5. 
| 11.6. 
| 11.7. 
| 11.8. 
| 11.9. 
| 11.10. 
| 11.11. 
| 11.12. 
| 11.13. 
| 11.14. 
| 11.15. 
| 11.16. 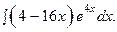
| 11.17. 
| 11.18. 
| 11.19. 
| 11.20. 
| 11.21. 
| 11.22. 
| 11.23. 
| 11.24. 
| 11.25. 
| 11.26. 
| 11.27. 
| 11.28. 
| 11.29. 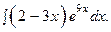
| 11.30. 
|
Найти неопределенный интеграл.
12.1. 
| 12.2. 
| 12.3. 
| 12.4. 
| 12.5. 
| 12.6. 
| 12.7. 
| 12.8. 
| 12.9. 
| 12.10. 
| 12.11. 
| 12.12. 
| 12.13. 
| 12.14. 
| 12.15. 
| 12.16. 
| 12.17. 
| 12.18. 
| 12.19. 
| 12.20. 
| 12.21. 
| 12.22. 
| 12.23. 
| 12.24. 
| 12.25. 
| 12.26. 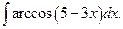
| 12.27. 
| 12.28. 
| 12.29. 
| 12.30. 
|
Найти неопределенный интеграл.
13.1. 
| 13.2. 
| 13.3. 
| 13.4. 
| 13.5. 
| 13.6. 
| 13.7. 
| 13.8. 
| 13.9. 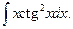
| 13.10. 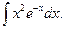
| 13.11. 
| 13.12. 
| 13.13. 
| 13.14. 
| 13.15. 
| 13.16. 
| 13.17. 
| 13.18. 
| 13.19. 
| 13.20. 
| 13.21. 
| 13.22. 
| 13.23. 
| 13.24. 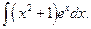
| 13.25. 
| 13.26. 
| 13.27. 
| 13.28. 
| 13.29. 
| 13.30. 
|
Найти неопределенный интеграл.
14.1. 
| 14.2. 
| 14.3. 
| 14.4. 
| 14.5. 
| 14.6. 
| 14.7. 
| 14.8. 
| 14.9. 
| 14.10. 
| 14.11. 
| 14.12. 
| 14.13. 
| 14.14. 
| 14.15. 
| 14.16. 
| 14.17. 
| 14.18. 
| 14.19. 
| 14.20. 
| 14.21. 
| 14.22. 
| 14.23. 
| 14.24. 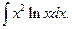
| 14.25. 
| 14.26. 
| 14.27. 
| 14.28. 
| 14.29. 
| 14.30. 
|
Найти неопределенный интеграл.
15.1. 
| 15.2. 
| 15.3. 
| 15.4. 
| 15.5. 
| 15.6. 
| 15.7. 
| 15.8. 
| 15.9. 
| 15.10. 
| 15.11. 
| 15.12. 
| 15.13. 
| 15.14. 
| 15.15. 
| 15.16. 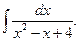
| 15.17. 
| 15.18. 
| 15.19. 
| 15.20. 
| 15.21. 
| 15.22. 
| 15.23. 
| 15.24. 
| 15.25. 
| 15.26. 
| 15.27. 
| 15.28. 
| 15.29. 
| 15.30. 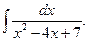
|
Найти неопределенный интеграл.
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|


 называется предел
называется предел  если предел существует. Если этот предел не существует, то не существует и несобственный интеграл. В этом случае принято говорить, что несобственный интеграл расходится. При существовании предела говорят, что несобственный интеграл сходится.
если предел существует. Если этот предел не существует, то не существует и несобственный интеграл. В этом случае принято говорить, что несобственный интеграл расходится. При существовании предела говорят, что несобственный интеграл сходится. ,
, .
. ,
,  и
и  относятся к несобственным интегралам I рода, т. к. для них не выполнено первое условие теоремы Ньютона-Лейбница, а именно один из пределов интегрирования или оба не являются конечными, а второе условие выполнено. Вычисление таких интегралов можно проводить по формуле (22), при этом
относятся к несобственным интегралам I рода, т. к. для них не выполнено первое условие теоремы Ньютона-Лейбница, а именно один из пределов интегрирования или оба не являются конечными, а второе условие выполнено. Вычисление таких интегралов можно проводить по формуле (22), при этом  считается как предельное значение, которое может быть конечным, бесконечным или не иметь смысла. То есть:
считается как предельное значение, которое может быть конечным, бесконечным или не иметь смысла. То есть: , (34)
, (34) , (35)
, (35) . (36)
. (36) .
.
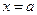 или в точке
или в точке 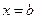 функция
функция 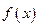 имеет бесконечный разрыв, то есть нарушается второе условие теоремы Ньютона-Лейбница, то интеграл
имеет бесконечный разрыв, то есть нарушается второе условие теоремы Ньютона-Лейбница, то интеграл  называется несобственным интегралом II рода.
называется несобственным интегралом II рода. в точке разрыва
в точке разрыва  равно предельному значению
равно предельному значению 
 .
. ,
, ,
,
 имеет бесконечный разрыв на отрезке
имеет бесконечный разрыв на отрезке  в точке
в точке  , т. к.
, т. к.  . Следовательно, данный интеграл является несобственным инетгралом II рода. Для его вычисления воспользуемся формулой (///) и получим:
. Следовательно, данный интеграл является несобственным инетгралом II рода. Для его вычисления воспользуемся формулой (///) и получим: ,
,
 имеет бесконечный разрыв на
имеет бесконечный разрыв на  в точке
в точке  т. к.
т. к.  .
.
 .
.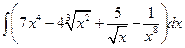 .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
.



















































































































































































 .
.




























 .
.





 .
.






 .
.








 .
.